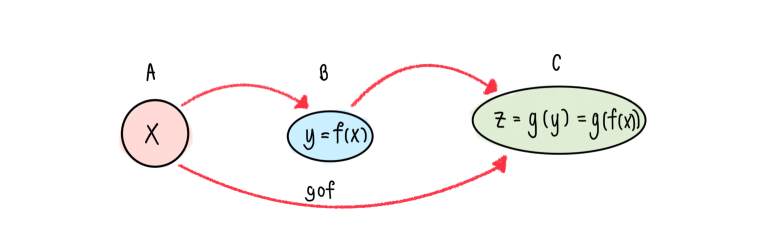
สัญลักษณ์แทนการบวก สัญลักษณ์แทนการบวก หรือ เรียกว่า ซิกมา ( Sigma ) เราใช้เพื่อลดรูปการบวกกันของตัวเลข เนื่องจากว่าบางทีเป็นการบวกของจำนวนตัวเลข 100 พจน์ ถ้ามานั่งเขียนทีละตัวก็คงจะเยอะไป เราจึงจะใช้เครื่องหมายซิกมามาใช้เพื่อประหยัดเวลาในการเขียนนั่นเอง เช่น 1 + 2 + 3 + 4 +5 สามารถเขียนแทนด้วย
อนุกรมเลขคณิต อนุกรมเลขคณิต คือการนำลำดับเลขคณิตแต่ละพจน์มาบวกกัน โดย เขียนแทนด้วย จากบทความ “สัญลักษณ์การบวก” ซึ่งเป็นการลดรูปการเขียนจำนวนหลายจำนวนบวกกัน ในบทความนี้จะพูดถึงการบวกของลำดับเลขคณิต การหาผลบวก สูตรสำหรับการหาผลบวกเลขคณิต สูตรอนุกรมเลขคณิต สูตรของอนุกรมเลขคณิตมีอยู่ 2 สูตร ดังนี้ 1) โดยที่ d คือ ผลต่างร่วม 2) โดยจะใช้สูตรนี้ก็ต่อเมื่อรู้ค่า
ลำดับ ลำดับ ( Sequence ) คือ เซตของจำนวนหรือตัวเลขที่เรียงกันเป็นระเบียบและมีเงื่อนไข เช่น ลำดับของจำนวนนับที่เพิ่มขึ้นทีละ 1 ก็จะสามารถเขียนได้เป็น 1, 2, 3, 4, … โดยตัวเลขเหล่านี้ เรียกว่า พจน์ ( Term ) เซตของลำดับจะเขีบยแทนด้วย และเราจะเรียก ว่าพจน์ที่
ลำดับเรขาคณิต ลำดับเรขาคณิต คือ ลำดับที่มีจำนวนเพิ่มขึ้นหรือลดลงอย่างคงที่เป็นจำนวนเท่า ซึ่งจำนวนที่เพิ่มขึ้นหรือลดลงนั้นเรียกว่า อัตราส่วนร่วม เขียนแทนด้วย r โดยที่ r = พจน์ขวาหารด้วยพจน์ซ้าย การเขียนลำดับเราจะเขียนแทนด้วย โดยที่ คือพจน์ทั่วไปหรือเรียกอีกอย่างว่า พจน์สุดท้ายนั่นเอง ตัวอย่างของลำดับเรขาคณิต 2, 4, 8, 16, 32, … จะได้ว่า
ลำดับเลขคณิต ลำดับเลขคณิต คือลำดับที่มีค่าเพิ่มขึ้นหรือลดลงอย่างคงที่ โดยจำนวนที่เพิ่มขึ้นหรือลดลงนี้เราเรียกว่าผลต่างร่วม แทนด้วยสัญลักษณ์ d โดยที่ d = พจน์ขวา – พจน์ซ้าย การเขียนลำดับเราจะเขียนแทนด้วย โดยที่ คือพจน์ทั่วไปหรือเรียกอีกอย่างว่า พจน์สุดท้ายนั่นเอง การหาพจน์ทั่วไปของลำดับเลขคณิต พจน์ที่1 n = 1
ฟังก์ชันตรีโกณมิติของมุม ฟังก์ชันตรีโกณมิติของมุม จะเกี่ยวข้องกับมุมที่มีหน่วยเป็นองศา (degree) และมุมที่มัหน่วยเป็นเรเดียน (radian) ในบทความนี้จะกล่าวถึงมุมทั้งหน่วยองศาและเรเดียน มุมฉาก การเปลี่ยนหน่วยของมุม สมบัติของฟังก์ชันตรีโกณมิติ และสามเหลี่ยมมุมฉาก ก่อนที่จะเริ่มเข้าสู่เนื้อหา พี่อยากให้น้องๆได้รู้พื้นฐานเกี่ยวกับฟังก์ชันตรีโกณมิติเพื่อที่จะได้เข้าใจเนื้อหาในบทความนี้มากขึ้น การวัดความยาวส่วนโค้ง ค่าของฟังก์ชันไซน์และโคไซน์ ฟังก์ชันตรีโกณมิติอื่นๆ หลังจากที่ไปทบทวนความรู้มาแล้วเรามาเริ่มเนื้อหาใหม่กันเลยค่ะ หน่วยของมุม 1.) องศา (degree) คือหน่วยของมุมในระนาบ 2 มิติ โดยที่
ฟังก์ชันตรีโกณมิติอื่นๆ ฟังก์ชันตรีโกณมิติอื่นๆ ในบทความนี้จะกล่าวถึงฟังก์ชันที่เป็นส่วนกลับของฟังก์ชันไซน์และโคไซน์ และฟังก์ชันที่เกิดจากการดำเนินการของค่า cosθ sinθ ซึ่งก็คือ tanθ และ cotθ นอกจากนี้ยังจะกล่าวถึงโคฟังก์ชันของฟังก์ชันตรีโกณมิติอีกด้วย ในบทความนี้สิ่งที่น้องๆต้องรู้ก็คือ วิธีการหาค่า cosθ และ sinθ จตุภาคของพิกัดจุดปลายส่วนโค้ง ซึ่งสามารถอ่านได้ตามลิงค์ด้านล่างนี้เลยค่ะ การวัดความยาวส่วนโค้ง ค่าของฟังก์ชันไซน์และโคไซน์ หลังจากที่น้องๆมีพื้นฐาน 2 เรื่องที่กล่าวมาแล้วเราจะเริ่มทำความรู้จักกับฟังก์ชันตรีโกณมิติอื่นๆกันค่ะ ฟังก์ชันที่เป็นส่วนกลับของฟังก์ชันไซน์และโคไซน์
ค่าของฟังก์ชันไซน์และโคไซน์ ค่าของฟังก์ชันไซน์และโคไซน์ จะเกี่ยวข้องกับ θ พิกัดของ จุด (x, y) ซึ่งในบทความนี้จะอธิบายเกี่ยวกับ ความสัมพันธ์ระหว่าง x, y กับ θ จากบทความที่ผ่านมาเราได้รู้จักวงกลมหนึ่งหน่วยและการวัดความยาวส่วนโค้ง ในบทความนี้น้องๆจะได้รู้จักกับฟังก์ชันไซน์ (sine function) และฟังก์ชันโคไซน์ (cosine function) และวิธีการหาค่าของฟังก์ชันทั้งสอง Sine function =
การวัดความยาวส่วนโค้ง การวัดความยาวส่วนโค้ง ในบทความนี้จะเป็นการวัดความยาวของวงกลม 1 หน่วย วงกลมหนึ่งหน่วย คือวงกลมที่มีจุดศูนย์กลางที่จุดกำเนิด และมีรัศมียาว 1 หน่วย จากสูตรของเส้นรอบวง คือ 2r ดังนั้นวงกลมหนึ่งหน่วย จะมีเส้นรอบวงยาว 2 และครึ่งวงกลมยาว จุดปลายส่วนโค้ง จากรูป จะได้ว่าจุด P เป็นจุดปลายส่วนโค้ง จากที่เราได้ทำความรู้จักกับวงกลมหนึ่งหน่วยและจุดปลายส่วนโค้งแล้ว
ระยะห่างของเส้นตรง ระยะห่างของเส้นตรง มีทั้งระยะห่างระหว่างจุดกับเส้นตรง และระหว่างเส้นตรงสองเส้นที่ขนานกัน ซึ่งจากบทความเรื่องเส้นตรง น้องๆพอจะทราบแล้วว่าเส้นตรงสองเส้นที่ขนานกันความชันจะเท่ากัน ในบทความนี้น้องๆจะทราบวิธีการหาระยะห่างของเส้นตรงที่ขนานกันด้วยซึ่งสามารถประยุกต์ใช้ในการหาสมการเส้นตรงได้ด้วย ระยะห่างระหว่างเส้นตรงกับจุด จากรูปจะได้ว่า โดยที่ A, B และ C เป็นค่าคงที่ และ A, B ไม่เป็นศูนย์พร้อมกัน ตัวอย่าง1 หาระยะห่างระหว่างจุด (1, 5) และเส้นตรง 2x
วงรี วงรี จะประกอบไปด้วย 1) แกนเอกคือแกนที่ยาวที่สุด และแกนโทคือแกนที่สั้นกว่า 2) จุดยอด 3) จุดโฟกัส ซึ่งจะแตกต่างกันไปแล้วแต่ว่าแกนใดเป็นแกนเอก 4) ความเยื้องศูนย์กลาง (eccentricity) วงรี ที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิด จากกราฟ สมการรูปแบบมาตรฐาน: จุดยอด : (a, 0) และ (-a,
พาราโบลา พาราโบลา คือเซตของจุดบนระนาบมีระยะห่างจากจุดโฟกัส (focus) เท่ากับระยะห่างจากเส้นไดเรกตริกซ์ (directrix) พาราโบลาที่มีจุดยอดอยู่ที่จุดกำเนิด กราฟของพาราโบลาจะมีลักษณะคล้ายระฆัง ตอนม.3 น้องๆเคยเห็นทั้งพาราโบลาหงายและคว่ำแล้ว แต่ในบทความนี้น้องๆจะได้รู้จักกับพาราโบลาตะแคงซ้ายและขวา สามารถเขียนเป็นตารางให้เข้าใจง่ายๆได้ดังนี้ ข้อสังเกต จะเห็นว่าถ้าแกนสมมาตรคือแกน y รูปแบบสมการของพาราโบลา y จะมีเลขชี้กำลังเป็น 1 สมการเส้นไดเรกตริกซ์ก็จะเกี่ยวข้องกับ y เช่นเดียวกับแกนสมมาตรเป็นแกน x รูปแบบสมการของพาราโบลา x
วงกลม วงกลม ประกอบด้วยจุดศูนย์กลาง (center) เส้นผ่านศูนย์กลาง และรัศมี (radius) สมการรูปแบบมาตรฐานของวงกลม สมการรูปแบบมาตรฐานของวงกลมที่มีจุดศูนย์กลางที่ (h, k) คือ (x-h)² + (y-k)² = r² จากสมการ จะได้ว่า มีจุดศูนย์กลางที่ (h, k) และรัศมี r จะเห็นว่าถ้าเรารู้สมการมาตรฐานเราจะรู้รัศมี
สมการเอกซ์โพเนนเชียล สมการเอกซ์โพเนนเชียล เป็นสมการที่จะมีเลขชี้กำลังเป็นตัวแปร เช่น , จากบทความที่ผ่านมาเราได้พูดถึงฟังก์ชันเอกซ์โพเนนเชียลไปแล้ว ในบทความนี้น้องๆจะได้เรียนรู้เกี่ยวกับการแก้สมการเอกซ์โพเนนเชียลซึ่งมีหลายวิธี ซึ่งเรื่องสมการเอกซ์โพเนนเชียลนี้มักจะออกสอบบ่อยเรียกได้ว่าทุกปีเลย ดังนั้นวันนี้เราเลยยจะมาสอนน้องๆแก้สมการ และให้เทคนิคการแก้สมการเอกซ์โพเนนเชียล สำหรับใครที่ยังไม่ได้ทำความรู้จักกับฟังก์ชันเอกซ์โพเนนเชียลสามารถเข้าไปดูตามลิงค์นี้เลยค่ะ !!!ฟังก์ชันเอกซ์โพเนนเชียล!!! การแก้สมการเอกซ์โพเนนเชียล วิธีที่ 1 : ทำฐานให้เหมือนกัน เมื่อฐานเท่ากันแล้ว เราก็จะได้ว่าเลขชี้กำลังก็จะเท่ากันด้วย ตัวอย่าง วิธีที่ 2 : ทำเลขชี้กำลังให้เหมือนกัน
จุด จุด เป็นตัวบอกตำแหน่งของสิ่งต่างๆ เช่น ตำแหน่งของสถานที่ต่างๆ ในเรื่องเรขาคณิตวิเคราะห์ จุดใช้บอกตำแหน่งในระนาบ 2 มิติ หรือ 3 มิติ เช่น ระยะทางระหว่างจุดสองจุด เราสามารถหาระยะทางระหว่างจุดสองจุดได้ โดยใช้สูตร โดยจะกำหนดให้ และ เป็นจุดในระนาบ เราจะได้ว่าระยะห่างระหว่างจุดทั้งสองหาได้จาก ตัวอย่าง ระยะห่างระหว่าง A(1,1) และ
เส้นตรง เส้นตรง มีสมการรูปแบบทั่วไปคือ Ax + By + C = 0 และสมการรูปแบบมาตรฐานของเส้นตรงจะเขียนอยู่ในรูป y = mx + C ซึ่งจะอยู่ในหัวข้อ “สมการเส้นตรง” เส้นตรงหนึ่งเส้นประกอบไปด้วยจุดหลายจุด ซึ่งจุดเหล่านี้จะทำให้เราสามารถหาความชันได้ และเมื่อเราทราบความชันก็จะสามารถหาสมการเส้นตรงได้นั่นเอง ความชันของเส้นตรง ความชันของเส้นตรง ส่วนใหญ่นิยมใช้ m
ดีเทอร์มิแนนต์ ดีเทอร์มิแนนต์ (Determinant) คือ ค่าของตัวเลขที่สอดคล้องกับเมทริกซ์จัตุรัส ถ้า A เป็นเมทริกซ์จัตุรัส จะเขียนแทนดีเทอร์มิแนนต์ของ A ด้วย det(A) หรือ โดยทั่วไปการหาค่าดีเทอร์มิแนนต์ที่เจอในข้อสอบจะไม่เกินเมทริกซ์ 3×3 เพราะถ้ามากกว่า 3 แล้ว จะเริ่มมีความยุ่งยาก **ค่าของดีเทอร์มิแนนต์จะเป็นจำนวนจริงและมีเพียงค่าเดียวเท่านั้นที่จะสอดคล้องกับเมทริกซ์จัตุรัส เช่น เมทริกซ์ B ก็จะมีค่าดีเทอร์มิแนนต์เพียงค่าเดียวเท่านั้น**
การบวก ลบ และคูณเมทริกซ์ การบวก ลบ และคูณเมทริกซ์ เราจะนำสมาชิกของเมทริกซ์แต่ละเมทริกซ์มาบวก ลบ คูณกัน ซึ่งการดำเนินการเหล่านี้มีสมบัติและข้อยกเว้นต่างกันไป เช่น การบวกต้องเอาสมาชิกตำแหน่งเดียวกันมาบวกกัน เป็นต้น ต่อไปเราจะมาดูวิธีการบวก ลบ และคูณเมทริกซ์กันค่ะ การบวกเมทริกซ์ เมทริกซ์ที่จะนำมาบวกกันได้นั้น ต้องมีมิติเท่ากัน และการบวกจะนำสมาชิกตำแหน่งเดียวกันมาบวกกัน เช่น 1.) 2.) การลบเมทริกซ์ การลบเมทริกซ์จะคล้ายๆกับการบวกเมทริกซ์เลย
ระบบสมการเชิงเส้น ระบบสมการเชิงเส้น คือระบบสมการที่มีดีกรีเป็นหนึ่ง ซึ่งก็คือเลขชี้กำลังของตัวแปรเป็นหนึ่งนั่นเอง ซึ่งในตอนมัธยมต้นน้องๆได้เรียนระบบสมการเชิงเส้น 2 ตัวแปรไปแล้ว ระบบสมการเชิงเส้นสองตัวแปร เช่น แล้วเราก็แก้สมการหาค่า x, y (ซึ่งอาจจะมีคำตอบหรือไม่มีก็ได้) แต่ในบทความนี้น้องๆจะได้เรียนรู้เกี่ยวกับระบบสมการเชิงเส้น n ตัวแปร นั่นก็คือน้องๆจะต้องหาคำตอบของตัวแปร n ตัวตัว ซึ่งการหาคำตอบนั้นมีหลายวิธีไม่ว่าจะเป็นการใช้เมทริกซ์ (ซึ่งน้องๆจะได้เรียนในบทความถัดๆไป) หรือการแก้สมการธรรมดาและในข้อสอบส่วนใหญ่จะเน้นให้น้องๆหาคำตอบในระบบสมการเชิงเส้นที่ไม่เกิน 3 ตัวแปร เพราะถ้าเกินกว่านั้นอาจจะใช้เวลาในการหาคำตอบมาก
เมทริกซ์ เมทริกซ์ (Matrix) คือตารางสี่เหลี่ยมที่บรรจุตัวเลขหรือตัวแปร สามารถนำมาบวก ลบ คูณกันได้ เราสามารถใช้เมทริกซ์ในการการแก้ระบบสมการเชิงเส้นได้ซึ่งจะสะดวกกว่าการแก้แบบกำจัดตัวแปรสำหรับสมการที่มากกว่า 2 ตัวแปร ตัวอย่างการเขียนเมทริกซ์ เรียกว่าเมทริกซ์มิติ 3×3 ซึ่ง 3 ตัวหน้าคือ จำนวนแถว 3 ตัวหลังคือ จำนวนหลัก ซึ่งเราจะเรียกแถวในแนวนอนว่า แถว และเรียกแถวในแนวตั้งว่า หลัก และจากเมทริกซ์ข้างต้นจะได้ว่า
ฟังก์ชันลอการิทึม ฟังก์ชันลอการิทึม คือฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียล จากที่ฟังก์ชันเอกซ์โพเนนเชียลคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์ที่ส่งจากจำนวนจริงไปยังจำนวนจริงบวก โดยที่ ดังนั้นฟังก์ชันดังกล่าวซึ่งเป็นฟังก์ชันผกผันของเอกซ์โพเนนเชียล ก็คือ คู่อันดับ (y, x) หรืออาจจะบอกได้อีกแบบคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์จากจำนวนจริงบวกไปยังจำนวนจริง โดยที่ จัดรูปใหม่ ได้เป็น (อ่านว่าล็อก x ฐาน
ฟังก์ชันเอกซ์โพเนนเชียล ฟังก์ชันเอกซ์โพเนนเชียล คือ ฟังก์ชันที่เขียนอยู่ในรูป {(x, y) ∈ × : y = } โดยที่ a เป็นจำนวนจริงที่มากกว่า 0 และ a ≠ 1 เช่น , , ซึ่งพูดอีกอย่างก็คือ
รากที่ n ของจำนวนจริง รากที่ n ของจำนวนจริง คือจำนวนจริงตัวหนึ่งยกกำลัง n แล้วเท่ากับ x เมื่อ n > 1 เราสามารถตรวจสอบรากที่ n ได้ง่ายๆ โดยนิยามดังนี้ นิยาม ให้ x, y เป็นจำนวนจริง และ n
เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะมีความเกี่ยวข้องกับกรณฑ์ในบทความ จำนวนจริงในรูปกรณฑ์ จากที่เรารู้ว่า จำนวนตรรกยะคือจำนวนที่สามารถเขียนอยู่ในรูปเศษส่วนของจำนวนเต็มได้ เช่น , , , 2 , 3 เป็นต้น ดังนั้นเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ ก็คือจำนวนจริงใดๆยกกำลังด้วยจำนวนที่สามารถเขียนในรูปเศษส่วนของจำนวนเต็ม เช่น , เป็นต้น โดยนิยามของเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ คือ เมื่อ k และ
ฟังก์ชันประกอบ ฟังก์ชันประกอบ คือฟังก์ชันที่เกิดจากการหาค่าฟังก์ชันที่ส่งจากเซต A ไปเซต C โดยที่ f คือฟังก์ชันที่ส่งจาก A ไปยัง B และ g เป็นฟังก์ชันที่ส่งจาก B ไปยัง C เราเรียกฟังก์ชันที่ส่งจาก A ไป C นี้ว่า gof จากรูป
การดำเนินการของฟังก์ชัน การดำเนินการของฟังก์ชัน ประกอบไปด้วย การบวก การลบ การคูณ และการหารของฟังก์ชัน ซึ่งเมื่อเราดำเนินการที่กล่าวมาข้างต้นกับฟังก์ชันแล้วจะทำให้เกิดฟังก์ชันใหม่ขึ้นมา เขียนแทนด้วย f + g, f – g, fg , ตามลำดับ โดยที่ (f + g)(x) = f(x)
ฟังก์ชันเพิ่มและฟังก์ชันลด ฟังก์ชันเพิ่มและฟังก์ชันลด สามารถตรวจสอบได้จากกราฟและนิยาม สมการหนึ่งสมการอาจจะเป็นทั้งฟังก์ชันเพิ่มและฟังก์ชันลดขึ้นอยู่กับรูปแบบของกราฟและสมการ บทนิยาม ให้ f เป็นฟังก์ชันที่ส่งจากโดเมนของฟังก์ชันไปยังจำนวนจริง โดยที่ A เป็นสับเซตของจำนวนจริง และ A เป็นสับเซตของโดเมน จะบอกว่า f เป็นฟังก์ชันเพิ่มบนเซตเซต A ก็ต่อเมื่อ สำหรับ และ ใดๆใน A ถ้า <
แบบฝึกหัดความสัมพันธ์ แบบฝึกหัดความสัมพันธ์ เป็นการทบทวนเนื้อหาเกี่ยวกับความสัมพันธ์ ได้แก่ เรื่องโดเมนและเรนจ์ของความสัม กราฟของความสัมพันธ์ และตัวผกผันของความสัมพันธ์ ก่อนทำแบบฝึกหัดความสัมพันธ์ บทความที่น้องๆควรรู้ คือ โดเมนของความสัมพันธ์ เรนจ์ของความสัมพันธ์ กราฟของความสัมพันธ์ ตัวผกผันของความสัมพันธ์ แบบฝึกหัด 1.) ถ้า (x, 5) = (3, x – y)
ฟังก์ชันผกผัน ฟังก์ชันผกผัน หรืออินเวอร์สฟังก์ชัน เขียนแทนด้วย เมื่อ เป็นฟังก์ชัน จากที่เรารู้กันว่า ฟังก์ชันนั้นเป็นความสัมพันธ์ ดังนั้นฟังก์ชันก็สามารถหาตัวผกผันได้เช่นกัน แต่ตัวผกผันนั้นไม่จำเป็นที่จะต้องเป็นฟังก์ชันเสมอไป เพราะอะไรถึงไม่จำเป็นจะต้องเป็นฟังก์ชัน เราลองมาดูตัวอย่างกันค่ะ ให้ f = {(1, 2), (3, 2), (4, 5),(6, 5)} จะเห็นว่า f เป็นฟังก์ชัน
ตัวผกผันของความสัมพันธ์ ตัวผกผันของความสัมพันธ์ r คือความสัมพันธ์ใหม่ที่เกิดจากการสลับตำแหน่งของสมาชิกตัวหน้ากับสมาชิกตัวหลังของคู่อันดับทุกคู่ในความสัมพันธ์ r เขียนแทนด้วย ซึ่ง = {(y, x) : (x, y ) ∈ r} เช่น r = {(1, 2), (3, 4), (5,
เรนจ์ของความสัมพันธ์ เรนจ์ของความสัมพันธ์ r คือ สมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหลัง เช่น = {(2, 2), (3, 5), (8, 10)} จะได้ว่า = {2, 5,
โดเมนของความสัมพันธ์ โดเมนของความสัมพันธ์ r คือ สมาชิกตัวหน้าของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหน้า เช่น = {(2, 2), (3, 4), (8, 9)} จะได้ว่า = {2, 3, 8}
กราฟของความสัมพันธ์ กราฟของความสัมพันธ์ r คือเซตของจุดในระนาบx, y โดยที่แต่ละจุดคือสมาชิกของความสัมพันธ์ r นั่นเอง อธิบายให้เข้าใจง่ายคือ เมื่อเราได้เซตของความสัมพันธ์ r ที่มีสมาชิกในเซตคือคู่อันดับแล้ว เราก็นำคู่อันดับแต่ละคู่มาเขียนกราฟนั่นเอง เช่น r = {(1, 1), (1, 2), (2, 2), (3, 4)} นำมาเขียนกราฟของความสัมพันธ์
ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง เป็นการส่งสมาชิกจากของเซตหนึ่งเรียกเซตนั้นว่าโดเมน ส่งไปให้สมาชิกอีกเซตหนึ่งเซตนั้นเรียกว่าเรนจ์ จากบทความก่อนหน้าเราได้พูดถึงฟังก์ชันและการส่งสมาชิกในเซตไปแล้วบางส่วน ในบทความนี้เราจะได้ทำความเข้าใจเกี่ยวกับฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งมากขึ้น จากที่เรารู้ว่าเซตของคู่อันดับเซตหนึ่งจะเป็นฟังก์ชันได้นั้น สมาชิกตัวหน้าต้องไปเหมือนกัน แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งเป็นการกำหนดขอบเขตให้ฟังก์ชันนั้นแคปลงกว่าเดิม เช่น {(1, a), (2, b), (3, a), (4, c)} จากเซตของคู่อันดับเราสมารถตอบได้เลยว่าเป็นฟังก์ชัน เพราะสมาชิกตัวหน้าไม่เหมือนกัน แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง คือการที่เรามีเซต 2 เซต แล้วเราส่งสมาชิกในเซตหนึ่งไปอีกเซตหนึ่ง
การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ คือการตรวจสอบคู่อันดับว่าคู่ไหนเป็นความสัมพันธ์ที่ตรงกับเงื่อนไขที่กำหนด จากที่เรารู้กันในบทความเรื่อง ความสัมพันธ์ว่า r จะเป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A × B แต่ถ้าเราใส่เงื่อนไขบางอย่างเข้าไป ความสัมพันธ์ r ที่ได้ก็อาจจะจะเปลี่ยนไปด้วย แต่ยังคงเป็นสับเซตของ A × B เหมือนเดิม
ความสัมพันธ์ ความสัมพันธ์ เกิดจากสิ่งสองสิ่งมาเกี่ยวข้องกันภายใต้กฎเกณฑ์บางอย่าง เช่น ความสัมพันธ์ของ a กับ b ซึ่ง a มากกว่า b เป็นต้น ก่อนที่เราจะเริ่มเนื้อหาของความสำคัญพี่อยากให้น้องๆรู้จักกับคู่อันดับ และผลคูณคาร์ทีเซียนก่อนนะคะ คู่อันดับ ในการเขียนคู่อันดับเป็นสิ่งที่ค่อนข้างสำคัญเลยทีเดียว เพราะถ้าน้องๆเขียนคู่อันดับผิดตำแหน่งนั่นหมายความว่า ความหมายของมันจะเปลี่ยนไปทันที เช่น คู่อันดับ (x, y) โดย x
ฟังก์ชันและกราฟของฟังก์ชัน ฟังก์ชันและกราฟของฟังก์ชัน มีความเกี่ยวข้องกันเนื่องจากฟังก์ชันที่เราเขียนในรูป y = f(x) สามารถนำไปเขียนกราฟในระบบพิกัดฉากได้ ซึ่งกราฟในระบบพิกัดฉากก็คือ กราฟที่ประกอบไปด้วยแกน x และ แกน y ก่อนที่เราจะเริ่มบทเรียนของฟังก์ชัน อยากให้น้องๆได้ศึกษารูปต่อไปนี้ก่อนนะคะ จากรูป คือการส่งสมาชิกในเซต A ไปยังสมาชิกในเซต B เซต A จะถูกเรียกว่า โดเมน
ข้อสอบO-Net ข้อสอบO-Net ในบทความนี้จะคัดเฉพาะเรื่องจำนวนจริงมาให้น้องๆทุกคนได้ดูว่าที่ผ่านมาแต่ละปีข้อสอบเรื่องจำนวนจริงออกแนวไหนบ้าง โดยบทความนี้พี่ได้นำข้อสอบย้อนหลังของปี 49 ถึงปี 52 มาให้น้องๆได้ดูพร้อมเฉลยอย่างละเอียด เมื่อน้องๆได้ศึกษาโจทย์ทั้งหมดและลองฝึกทำด้วยตัวเองแล้ว น้องๆจะสามารถทำข้อสอบทั้งของในโรงเรียนและข้อสอบO-Net ได้แน่นอนค่ะ ข้อสอบO-Net เรื่องจำนวนจริง ปี 49 1. มีค่าเท่ากับข้อในต่อไปนี้ 60
จากบทความที่ผ่านมา น้องๆได้ศึกษาเรื่องค่าสัมบูรณ์และการแก้อสมการไปแล้ว บทความนี้จะเป็นการเอาเนื้อหาของอสมการและค่าสัมบูรณ์มาปรับใช้ นั่นก็คือ เราจะแก้อสมการของค่าสัมบูรณ์นั่นเองค่ะ เรื่องอสมการค่าสัมบูรณ์น้องๆจะได้เจอในข้อสอบ O-Net แต่น้องๆไม่ต้องกังวลค่ะ ถ้าน้องๆเข้าใจหลักการและสมบัติของค่าสัมบูรณ์และอสมการน้องๆจะสามารถทำข้อสอบได้แน่นอน
จากบทความที่ผ่านมาได้พูดถึงเรื่องช่วงของจำนวนจริงไปแล้ว บทความนี้เราจะนำความรู้เกี่ยวกับช่วงของจำนวนจริงมาใช้ในการแก้อสมการเพื่อหาคำตอบกันนะคะ ถ้าน้องๆได้อ่านบทความนี้แล้วรับรองว่าพร้อมทำข้อสอบแน่นอนค่ะ
ค่าสัมบูรณ์ ค่าสัมบูรณ์ หรือ Absolute คือค่าของระยะทางจากศูนย์ไปยังจุดที่เราสนใจ เช่น ระยะทางจากจุด 0 ถึง -5 มีระยะห่างเท่ากับ 5 เนื่องจากค่าสัมบูรณ์เอาไว้บอกระยะห่าง ดังนั้นค่าสัมบูรณ์จะมีค่าเป็นบวกหรือศูนย์เท่านั้น ไม่สามารถเป็นลบได้ นิยามของค่าสัมบูรณ์ ให้ a เป็นจำนวนจริงใดๆ จะได้ว่า และ น้องๆอาจจะงงๆใช่ไหมคะ ลองมาดูตัวอย่างสักนิดนึงดีกว่าค่ะ เช่น เพราะ
จำนวนจริงในรูปกรณฑ์ จำนวนจริงในรูปกรณฑ์ หรือราก เขียนแทนด้วย อ่านว่า รากที่ n ของ x หรือ กรณฑ์ที่ n ของ x เราจะบอกว่า จำนวนจริง a เป็นรากที่ n ของ x ก็ต่อเมื่อ เช่น 2 เป็นรากที่
ช่วงของจำนวนจริง ช่วงของจำนวนจริง เอาไว้บอกขอบเขตของตัวแปรตัวแปรหนึ่ง เช่น x เป็นตัวแปรที่ไม่ทราบค่า a, b เป็นค่าคงที่ใดๆ a < x < b หมายความว่า ค่าของ x อยู่ระหว่าง a ถึง b เป็นต้น ช่วงของจำนวนจริง ประกอบไปด้วย ช่วงเปิดและช่วงปิด
การแก้สมการกำลังสอง การแก้สมการกำลังสอง สามารถทำได้โดยการ แยกตัวประกอบพหุนามกำลังสอง และใช้สูตร เราแก้สมการเพื่อหาคำตอบหรือหาค่าของตัวแปร ในบทความนี้พี่จะพูดถึงสมการกำลังสองตัวแปรเดียว ซึ่งอยู่ในรูป ax² + bx + c = 0 โดยที่ a, b, c เป็นค่าคงตัว และ a ≠ 0 ตัวอย่างสมการกำลังสองตัวแปรเดียว
การแยกตัวประกอบพหุนาม การแยกตัวประกอบพหุนาม เป็นการแยกตัวประกอบของสมการเพื่อให้ง่ายต่อการหาคำตอบของสมการที่จะต้องเรียนในเนื้อหาถัดไป ในบทความนี้จะพูดถึงพหุนามดีกรี 2 ตัวแปรเดียว พหุนามดีกรี 2 คือ พหุนามที่มีเลขยกกำลังสูงสุด คือ 2 พหุนามดีกรี 2 ตัวแปรเดียว คือ พหุนามที่มีเลขยกกำลังสูงสุดคือ 2 และ มีตัวแปร 1 ตัว เขียนอยู่ในรูป ax² +
ระบบจำนวนจริง “ระบบจำนวนจริง” เป็นรากฐานสำคัญของวิชาคณิตศาสตร์ ประกอบไปด้วยจำนวนต่างๆ ได้แก่ จำนวนตรรกยะ จำนวนอตรรกยะ จำนวนเต็ม จำนวนนับ โครงสร้าง ระบบจำนวนจริง มนุษย์เรามีความคิดเรื่องจำนวนและระบบการนับมาตั้งแต่โบราณ และจำนวนที่มนุษย์เรารู้จักเป็นอย่างแรกก็คือ จำนวนนับ การศึกษาระบบของจำนวนจึงใช้พื้นฐานของจำนวนนับในการสร้างจำนวนอื่นขึ้นมา จนกลายมาเป็นจำนวนจริง และจำนวนเชิงซ้อน (เนื้อหาม.5) ดังนั้น ถ้าน้องๆเข้าใจจำนวนนับแล้วน้องๆก็จะสามารถศึกษาระบบจำนวนอื่นๆได้ง่ายขึ้น โครงสร้าง จำนวนจริง จำนวนจริงคือจำนวนที่ประกอบไปด้วย
สมบัติการบวกจำนวนจริง สมบัติการบวกจำนวนจริง เป็นสมบัติที่น้องๆต้องรู้ เพราะเป็นรากฐานของวิชาคณิตศาสตร์และน้องๆจะต้องใช้สมบัติพวกนี้ในการเรียนคณิตศาสตร์ในระดับที่สูงขึ้น สมบัติการบวกของจำนวนจริง มีทั้งหมด 5 ข้อ ดังนี้ 1.) สมบัติปิดการบวก สมบัติปิดการบวก คือ การที่เรานำจำนวนจริง 2 ตัวมาบวกกัน เราก็ยังได้ผลลัพธ์เป็นจำนวนจริงเหมือนเดิม เช่น 1 + 2 = 3 จะเห็นว่า
จากบทความก่อนหน้านี้น้องๆได้เรียนเรื่องสมบัติการบวกจำนวนจริงไปแล้ว บทความนี้พี่ก็จะพูดถึงสมบัติการคูณจำนวนจริงซึ่งมีเนื้อหาคล้ายๆกันกับการบวก และมีเพิ่มสมบัติการแจกแจงเข้ามา เนื้อหาเหล่านี้ล้วนเป็นพื้นฐานสำคัญที่จะใช้ในการเรียนเนื้อหาบทต่อๆไป เมื่อน้องๆอ่านบทความนี้แล้วน้องๆจะเรียนเนื้อหาบทต่อๆไปได้ง่ายขึ้นแน่นอนค่ะ
แบบฝึกหัดการให้เหตุผล แบบฝึกหัดการให้เหตุผล ประกอบไปด้วยการให้เหตุผลแบบอุปนัยและการให้เหตุผลแบบนิรนัย ซึ่งแบบฝึกหัดนี้จะช่วยให้น้องๆได้ฝึกฝนการทำโจทย์จนน้องๆเชี่ยวชาญและส่งผลให้น้องๆทำข้อสอบได้แบบไม่ผิดพลาด ถ้าเรารู้เฉยๆเราอาจจะทำข้อสอบได้แต่การที่เราฝึกทำโจทย์ด้วยจะทำให้เราทำข้อสอบได้แน่นอนค่ะ แบบฝึกหัดเพิ่มเติมและข้อสอบ O-Net ตัวอย่างต่อไปนี้เป็นข้อสอบ O-Net ของปีก่อนๆ 1.) พิจารณาการอ้างเหตุผลต่อไปนี้ ก. เหตุ 1. ถ้าฝนไม่ตกแล้วเดชาไปโรงเรียน 2. ฝนตก ผล
จากบทความที่ผ่านมาเราเรียนเรื่องการให้เหตุผลแบบนิรนัย บทความนี้เป็นเนื้อหาเรื่องการตรวจสอบความสมเหตุสมผลซึ่งมักจะออกสอบทั้งในโรงเรียนและ O-Net หลังจากน้องๆได้อ่านบทความนี้แล้วน้องๆจะทำข้อสอบได้แน่นอนค่ะ
จากบทความที่แล้วเราได้เรียนเรื่องการให้เหตุผลแบบอุปนัยไปแล้ว บทความนี้พี่จะพูดถึงการให้เหตผลแบบนิรนัย ซึ่งแน่นอนว่ามักจะเจอในข้อสอบ O-Net แต่น้องๆไม่ต้องกังวลว่าจะทำไม่ได้ หากน้องได้อ่านบทความนี้แล้วน้องๆจะทำข้อสอบเกี่ยวกับการให้เหตุผลได้แน่นอนค่ะ
การให้เหตุผลแบบอุปนัย การให้เหตุผลแบบอุปนัย คือ การนำประสบการณ์มาสรุปผล เช่น เราไปซื้อผลไม้แล้วเราชิมผลไม้ 2-3 ลูก ปรากฏว่า มีรสหวาน เราเลยสรุปว่าผลไม้ทั้งกองนั้นหวาน เป็นต้น ซึ่งการสรุปผลอาจจะเป็นจริงหรือเท็จก็ได้ อาจจะขึ้นอยู่กับประสบการณ์ของผู้สรุป ดังนั้น ผลสรุปไม่จำเป็นต้องเหมือนกัน ตัวอย่างเช่น เหตุ เมื่อวานแป้งตั้งใจเรียน วันนี้แป้งตั้วใจเรียน ผลสรุป พรุ่งนี้แป้งจะตั้งใจเรียน การให้เหตุผลแบบนี้ เหมือนเป็นการคาดคะเนเหตุการณ์ที่จะเกิดขึ้นต่อไป ซึ่งการคาดคะเนนี้อาจจะจริงหรือเท็จก็ได้
“สมมูลและนิเสธ” ของประโยคที่มีตัวบ่งปริมาณ สมมูลและนิเสธ เราเคยเรียนกันไปแล้วก่อนหน้านี้ แต่เป็นของประพจน์ p, q, r แต่ในบทความนี้จะเป็นสมมูลและนิเสธของประโยคที่มีตัวบ่งปริมาณ ซึ่งก็จะเอาเนื้อหาก่อนหน้ามาปรับใช้กับประโยคที่มีตัวบ่งปริมาณ สิ่งที่เราจะต้องรู้และจำให้ได้ก็คือ การสมมูลกันของประพจน์ เพราะจะได้ใช้ในบทนี้แน่นอนน ใครที่ยังไม่แม่นสามารถไปอ่านได้ที่ บทความรูปแบบของประพจน์ที่สมมูลกัน นิเสธของตัวบ่งปริมาณ เมื่อเราเติมนิเสธลงไปในประโยคที่มีตัวบ่งปริมาณ ข้อความต่อไปนี้จะสมมูลกัน กรณี 1 ตัวแปร ∼∀x[P(x)] ≡ ∃x[∼P(x)] ∼∃x[P(x)]
ตัวบ่งปริมาณ ตัวบ่งปริมาณ คือ สัญลักษณ์หรือข้อความที่เมื่อเราเอาไปเติมใน “ประโยคเปิด” แล้วจะทำให้ประโยคนั้นกลายเป็นประพจน์ ประโยคเปิด คือประโยคบอกเล่าหรือปฏิเสธที่ติดค่าตัวแปรที่ยัง “ไม่รู้ว่าเป็นจริงหรือเท็จ” โดยตัวแปรนั้นเป็นสมาชิกของเอกภพสัมพัทธ์ (Universe : U) ประโยคเปิด ยังไม่ใช่ประพจน์ (แต่เกือบเป็นแล้ว) เพราะเรายังไม่รู้ว่าเป็นจริงหรือเท็จ เช่น “x มากกว่า 3” จะเห็นว่าตัวแปร คือ x ซึ่งเราไม่รู้ว่า x
บทความนี้จะทำให้น้องๆเข้าใจหลักการอ้างเหตุผลมากขึ้นและสามารถตรวจสอบได้ว่า การอ้างเหตุผล สมเหตุสมผลหรือไม่
การสมมูลกันของประพจน์สำคัญอย่างไร?? ถือว่าสำคัญค่ะ เพราะถ้าเรารู้ว่าประพจน์ไหนสมมูลกับประพจน์อาจจะทำให้การตรวจสอบการเป็นสัจนิรันดร์และการหาค่าความจริงง่ายขึ้น หลังจากอ่านบทความนี้จบ น้องๆจะสามารถทำแบบฝึกหัดเรื่องการสมมูลได้และพร้อมทำข้อสอบได้แน่นอน
ในบทความจะเขียนเกี่ยวกับวิธีการพิสูจน์การเป็นสัจนิรันดร์ของประพจน์ ซึ่งจะเน้นให้น้องๆเข้าใจหลักการของการพิสูจน์ สิ่งที่น้องจะได้จากบทความนี้คือ น้องจะสามารถพิสูจน์การเป็นสัจนิรันดร์ของประพจน์ได้และหากน้องๆขยันทำโจทย์บ่อยๆจะทำให้น้องวิเคราะห์โจทย์เกี่ยวกับสัจนิรันดร์ได้ง่ายขึ้นแน่นอนค่ะ
บทความนี้เป็นเนื้อหาเกี่ยวกับการสร้างตารางค่าความจริงของประพจน์ เป็นเนื้อหาที่ไม่ยากมากหลังจากน้องๆได้อ่านบทความนี้แล้ว น้องๆจะสามารถสร้างตารางค่าความจริงได้ สามารถบอกได้ว่าประพจน์แต่ละประพจน์เป็นจริงได้กี่กรณีและเป็นเท็จได้กี่กรณี และจะทำให้น้องเรียนเนื้อหาเรื่องต่อไปได้ง่ายยิ่งขึ้น
สัญลักษณ์ของเซตจะช่วยให้เราไม่ต้องเขียนประโยคยาวซ้ำๆ และใช้ได้เกือบทุกบทของวิชาคณิตศาสตร์ ช่วยให้ประหยัดเวลาและเนื้อที่บนกระดาษมากๆ
บทความนี้เป็นเนื้อหาเกี่ยวกับประพจน์ การเชื่อมประพจน์ และการหาค่าความจริง ซึ่งเนื้อหาเหล่านี้เป็นภาษาของคณิตศาสตร์ เราจะเห็นตัวเชื่อมประพจน์ในทฤษฎีบทต่างๆในคณิตศาสตร์ หลังจากอ่านบทความนี้ น้องๆจะสามารถบอกได้ว่าข้อความไหนเป็นหรือไม่เป็นประพจน์ และน้องๆจะสามารถทำข้อสอบเกี่ยวกับตรรกศาสตร์ได้
จำนวนสมาชิกของเซตจำกัด เป็นเรื่องที่สามารถเอาไปใช้ในชีวิตประจำวันได้จริง และสิ่งที่น้องๆจะได้หลังจากอ่านบทความนี้คือ น้องๆจะสามารถทำโจทย์ปัญหาเกี่ยวกับจำนวนสมาชิกของเซตจำกัดได้ และอาจจะเอาไปประยุกต์ใช้ในชีวิตประจำวันได้ด้วย
การดำเนินการของเซตประกอบไปด้วย ยูเนียน อินเตอร์เซกชัน คอมพลีเมนต์ของเซต และผลต่าง เรื่องนี้เป็นอีกหนึ่งเรื่องที่เราจะได้ใช้ในบทต่อๆไป เรื่องนี้จึงค่อนข้างมีประโยชน์ในเรื่องของการเรียนเนื้อหาบทต่อไปง่ายขึ้น
บทความนี้จะเป็นเนื้อหาเกี่ยวกับสับเซต เพาเวอร์เซต ซึ่งเป็นเนื้อหาที่สำคัญ หลังจากที่น้องๆอ่านบทความนี้จบแล้ว น้องๆจะสามารถบอกได้ว่า เซตใดเป็นสับเซตของเซตใดและสามารถบอกได้ว่าสมาชิกของเพาเวอร์เซตมีอะไรบ้าง
เซตคืออะไร? เซต คือ คำที่ใช้เรียกกลุ่มของสิ่งต่างๆ ทำไมต้องเรียนเซต เซตมีประโยชน์ในเรื่องของการจำแนกสิ่งต่างๆออกเป็นกลุ่มๆ อีกทั้งยังแทรกอยู่ในเนื้อหาบทอื่นๆของคณิตศาสตร์ เราจึงจำเป็นต้องทำความเข้าใจเกี่ยวกับเซต เพื่อที่จะเรียนเนื้อหาบทอื่นๆได้ง่ายขึ้น ความรู้เบื้องต้นเกี่ยวกับเซต เซต คือคำที่ใช้เรียกกลุ่มของสิ่งต่างๆ เช่น เซตของสระในภาษาอังกฤษ คือ กลุ่มของสระในภาษาอังกฤษ a,e,i,o,u เป็นต้น สมาชิกของเซต คือ สิ่งที่อยู่ในเซต เช่น เซตของสระในภาษาอังกฤษ สมาชิกของเซต คือ
