- นักเรียนสามารถได้รับคะแนนสอบที่ดีจากการสอบที่โรงเรียน และสามารถเตรียมตัวในการเริ่มต้นสำหรับการเรียนในระดับชั้นแรกของระดับมัธยมศึกษาตอนปลาย
- ปลดล็อคคลิปทุกคลิป แบบฝึกหัด และฟีเจอร์แบบฝึกหัด
ติว ม.4 เรียนพิเศษ ออนไลน์

ผลตอบรับจากผู้ใช้งานจริง





















ประวัติการไลฟ์สอนยอดนิยม
สามารถกดย้อนดูคลิปที่เคยผ่านการไลฟ์สอนไปแล้ว เพื่อทบทวนอีกครั้ง
เตรียมสอบเข้า ม.4 MWIT วมว. จภ. ตอนที่ 2 สมบัติของเลขยกกำลังและราก (เสริม)
29 July 2025- + คณิตศาสตร์ (เพิ่มเติม)
- + ครูปาล์ม
- + ม.2
- + ม.3
- + ม.4
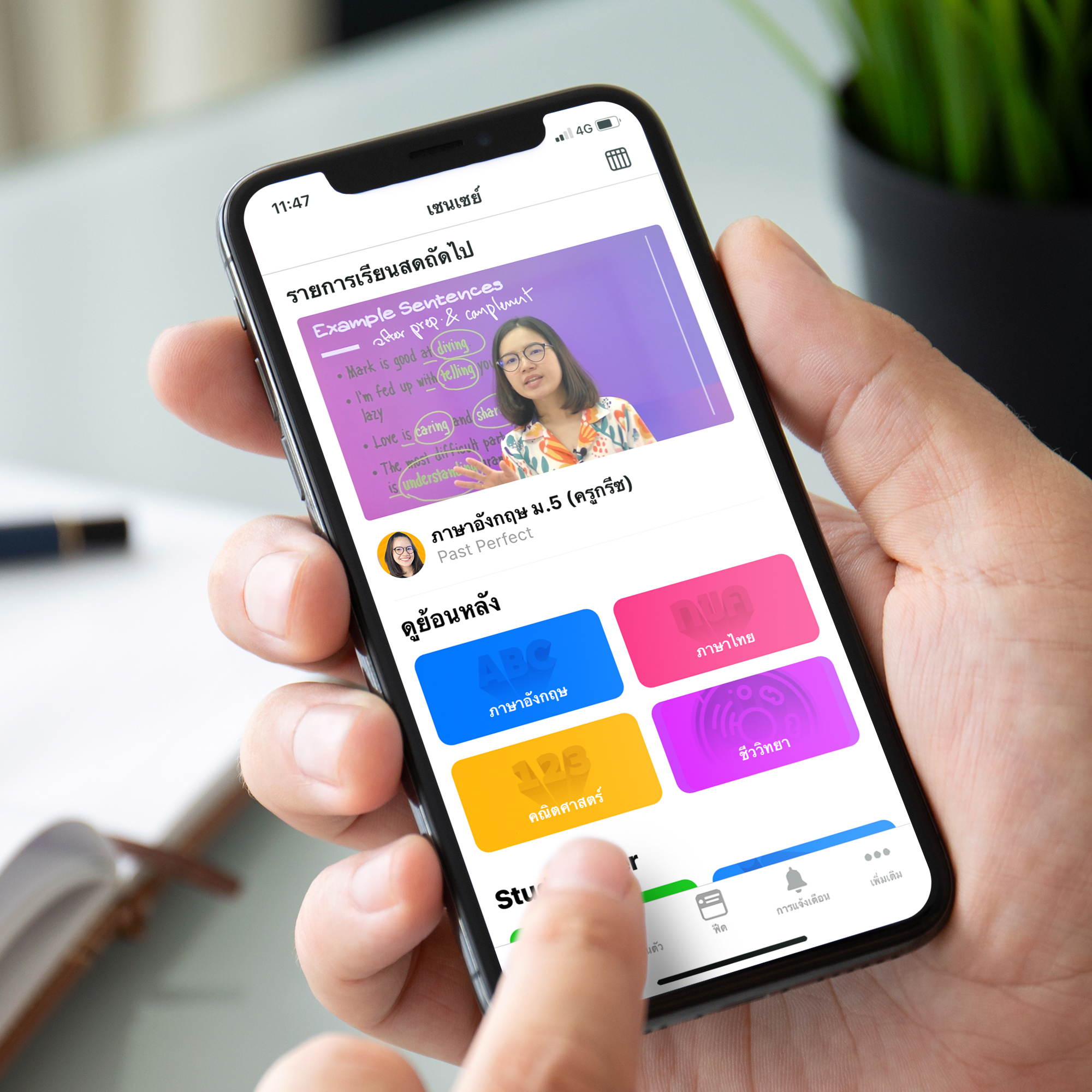
ดูได้ทั้ง 4 รายวิชา
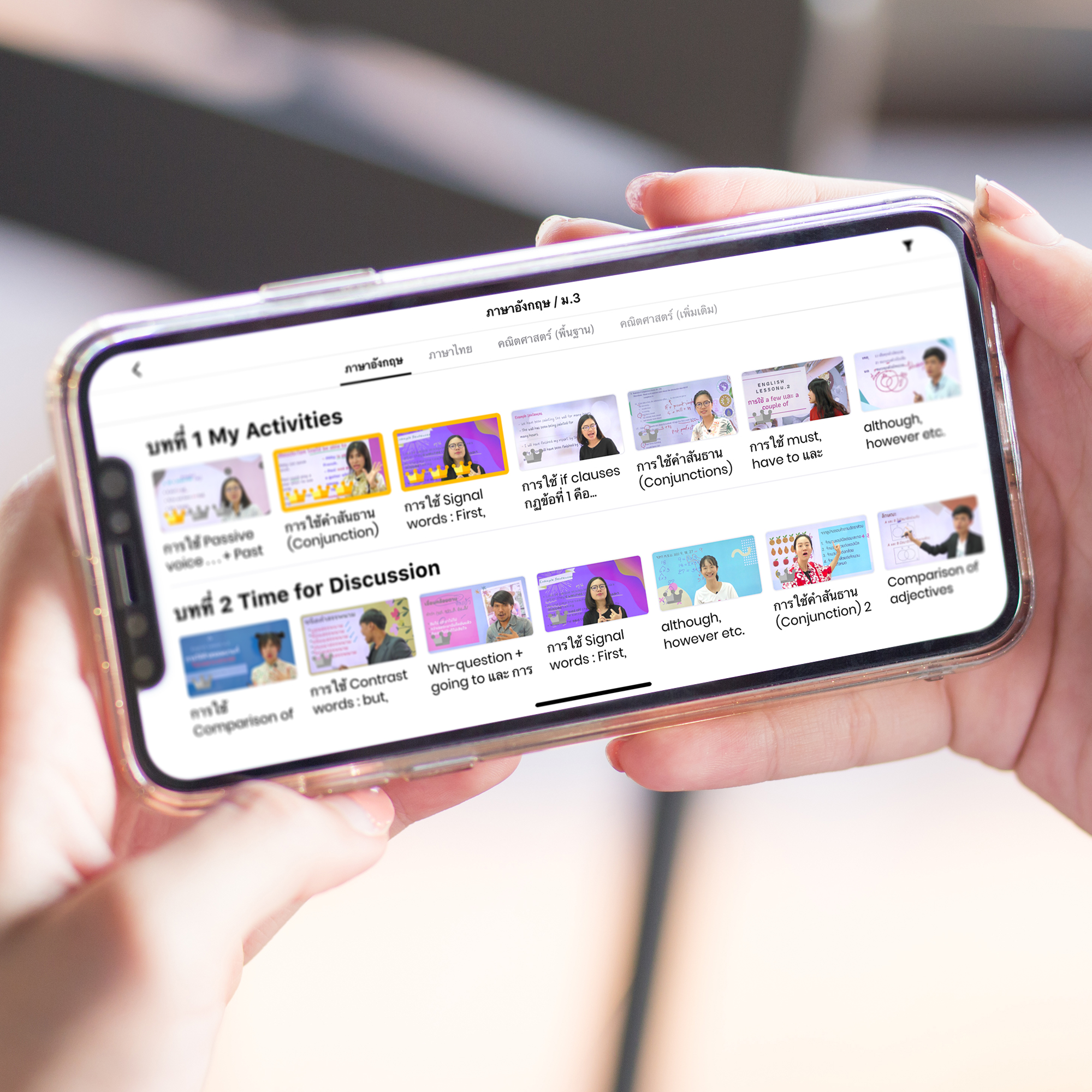
2,000+ คลิป และแบบทดสอบกว่า 4,000+ ข้อ
อัพเดทคลิปใหม่ๆ ทุกสัปดาห์ และคุณสามารถดูคลิปอะไรก็ได้ที่คุณต้องการจากเนื้อหาของเรา

บทเรียนแบบโต้ตอบ
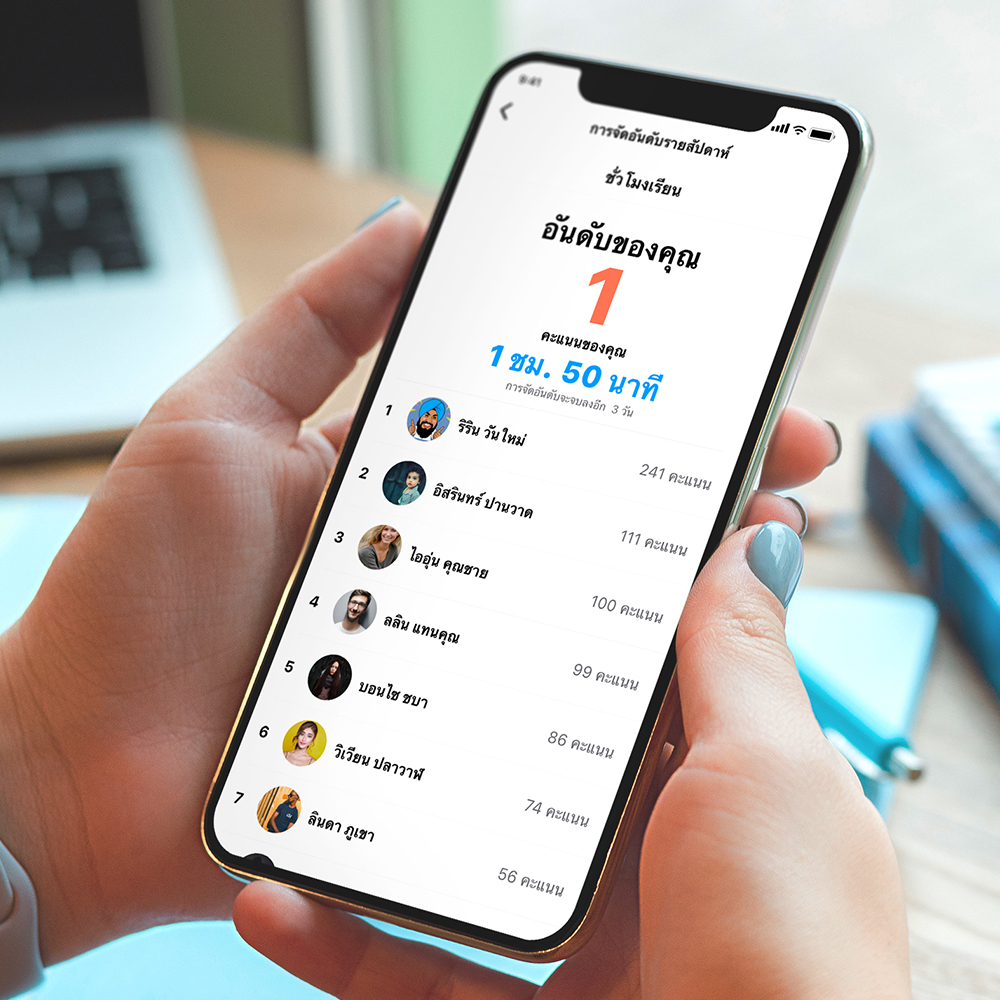
แข่งขันกับเพื่อนๆ
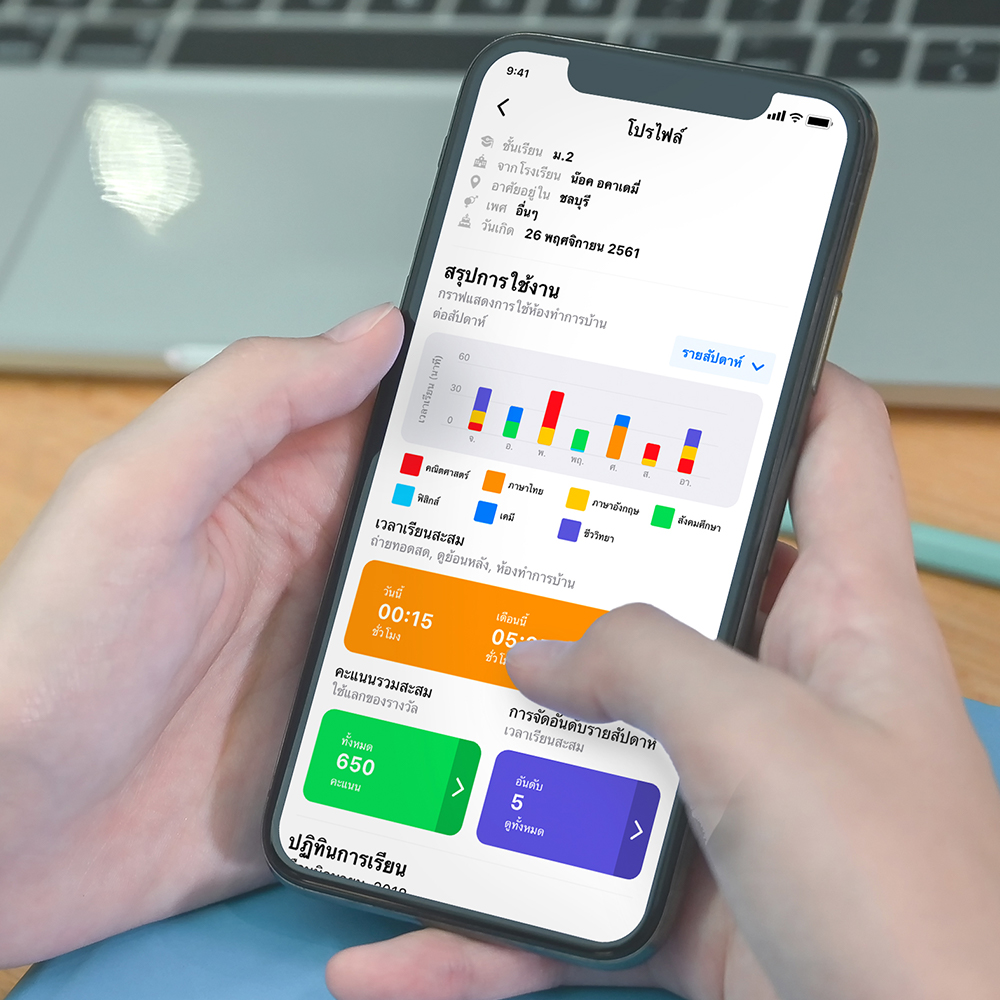
กราฟการเรียนรู้

ใช้ได้ทุกอุปกรณ์
บริการของเรา
ทดลองใช้งานฟรี 3 วัน เพื่อเข้าถึงบริการของเราได้แบบไม่จำกัดวิชา!
มีบทเรียนมากกว่า 2,000+ คลิป 4,000+ แบบฝึกหัด และ ดูประวัติการไลฟ์สอน ได้ไม่จำกัด บนทุกอุปกรณ์
- บัตรเครดิต
- พร้อมเพย์
- โอนเงินผ่านธนาคาร
- บัตรเครดิต
- บัตรเครดิต
- พร้อมเพย์
- โอนเงินผ่านธนาคาร
- บัตรเครดิต
- บัตรเครดิต
- พร้อมเพย์
- โอนเงินผ่านธนาคาร

บทความ ม.4

อิเหนา จากนิทานปันหยีสู่วรรณคดีเลื่องชื่อของไทย
อิเหนา เป็นวรรณคดีที่ถูกเผยแพร่เข้ามาในไทยตั้งแต่สมัยกรุงศรีอยุธยา น้อง ๆ สงสัยไหมคะว่าจุดเริ่มต้นของนิทานของชาวชวานี้มีจุดเริ่มต้นในไทยอย่างไร เหตุใดถึงถูกประพันธ์ขึ้นเป็นบทละครให้ได้เล่นกันในราชสำนัก ถ้าน้อง ๆ พร้อมหาคำตอบแล้ว เราไปเรียนรู้ประวัติความเป็นมาและเรื่องย่อของอิเหนา ตอน ศึกกะหมังกุหนิงกันเลยค่ะ ความเป็นมา อิเหนามีความเป็นมาจากนิทานปันหยี หรือที่เรียกว่า อิเหนาปันหยีรัตปาตี ซึ่งเป็นนิทานที่เล่าแพร่หลายกันมากในชวา เชื่อกันว่าเป็นนิยายอิงประวัติศาสตร์ของชวา ในสมัยพุทธศตวรรษที่ 16 ปรุงแต่งมาจากพงศาวดารชวา อิทธิพลของเรื่องอิเหนาเข้ามาในประเทศไทยครั้งแรกในสมัยอยุธยา จากการที่เจ้าฟ้าหญิงกุณฑลและเจ้าฟ้าหญิงมงกุฎ
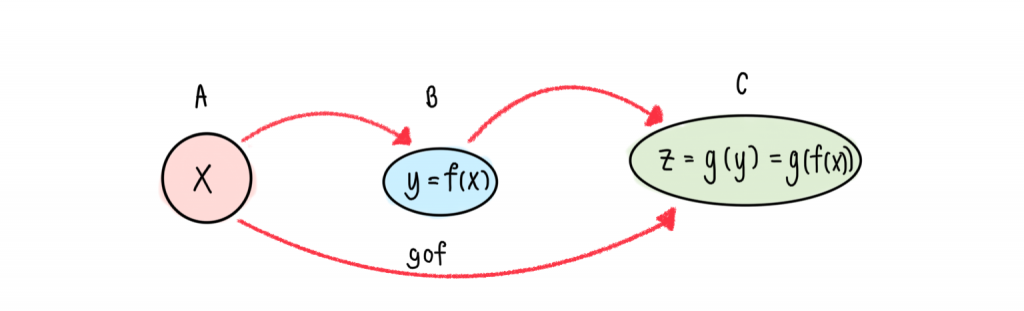
ฟังก์ชันประกอบ
ฟังก์ชันประกอบ ฟังก์ชันประกอบ คือฟังก์ชันที่เกิดจากการหาค่าฟังก์ชันที่ส่งจากเซต A ไปเซต C โดยที่ f คือฟังก์ชันที่ส่งจาก A ไปยัง B และ g เป็นฟังก์ชันที่ส่งจาก B ไปยัง C เราเรียกฟังก์ชันที่ส่งจาก A ไป C นี้ว่า gof จากรูป

เรียนรู้เทคนิคที่จะช่วยให้การเขียน ผังมโนภาพ เป็นเรื่องง่ายๆ
ผังมโนภาพ เป็นเทคนิคที่พัฒนาขึ้นจากจดบันทึกความคิด ความรู้ ความเข้าใจ น้อง ๆ หลายคนก็คงจะเคยได้รับโจทย์จากคุณครูให้เขียนแผนผังมโนภาพเพื่อทดสอบความเข้าใจ หลายคนอาจจะคิดว่าเป็นเรื่องยากที่จะเขียนออกมา แต่ทราบไหมคะว่าที่จริงแล้วมีวิธีการเขียนที่ง่ายมากแถมยังมีประโยชน์อีกด้วย จะเป็นอย่างไรไปเรียนรู้เรื่องนี้พร้อมกันเลยค่ะ ความหมายของผังมโนภาพ ผังมโนภาพเป็นแผนผังหรือแผนภาพที่แสดงความสัมพันธ์ของมโนทัศน์หรือความคิดรวบยอด ที่เริ่มจากความคิดหลัก ซึ่งทำหน้าที่เป็นชื่อเรื่อง แล้วแตกแขนงไปสู่ความคิดย่อย ๆ กระจายออกไปโดยรอบ ทำให้เกิดภาพเชื่อมโยงขององค์ความรู้เรื่องใดเรื่องหนึ่งในทุกแง่มุม วิธีเขียนแผนผังมโนภาพ ผังมโนภาพเป็นผังที่แสดงความสัมพันธ์ของสาระหรือความคิดต่าง




