บทความนี้ได้รวบรวมความรู้เรื่อง การทดลองสุ่มและเหตุการณ์ ซึ่งได้กล่าวถึงในลักษณะของความหมายและยกตัวอย่างประกอบ และอธิบายอย่างละเอียด ซึ่งก่อนจะเรียนเรื่อง การทดลองสุ่มและเหตุการณ์ น้องๆสามารถทบทวน ความน่าจะเป็น ได้ที่ ⇒⇒ ความน่าจะเป็น ⇐⇐
การทดลองสุ่ม
การทดลองสุ่ม คือ การทดลองซึ่งทราบว่าผลลัพธ์ที่จะเกิดขึ้นอาจจะเป็นอะไรได้บ้าง แต่ไม่สามารถบอกได้อย่างถูกต้องแน่นอนว่าในแต่ละครั้งที่ทำการทดลอง ผลที่เกิดขึ้นจากการทดลองจะเป็นอะไรในบรรดาผลลัพธ์ที่อาจเป็นไปได้เหล่านั้น เช่น
- การโยนเหรียญซึ่งมีผลลัพธ์ที่จะเกิดขึ้นได้ 2 แบบ คือ หัวหรือก้อย เมื่อโยนเหรียญ ให้ดีก็จะไม่สามารถทำนายผลลัพธ์ล่วงหน้าว่าจะออกหัวหรือก้อย
- การสับไพ่สำรับหนึ่งซึ่งมีไพ่ทั้งหมด 52 ใบ ถ้าดึงออกมาหนึ่งใบจะไม่สามารถบอกล่วงหน้าได้ว่าไพ่ใบนั้นเป็นไพ่ใบใด การดึงไพ่จากสำรับจึงเป็นการทดลองสุ่ม
การทดลองสุ่มแต่ละครั้ง จะมีผลลัพธ์เกิดขึ้นเสมอและอาจมีได้แตกต่างกัน ผลลัพธ์ทั้งหมดเหล่านั้นมีอะไรบ้าง หาได้จากการแจงนับ เช่น
- โยนเหรียญ 1 เหรียญ 1 ครั้ง ผลลัพธ์ที่อาจจะเกิดขึ้น คือ หัว หรือ ก้อย
- โยนลูกเต๋า 1 ลูก 1 ครั้ง ผลลัพธ์ที่อาจจะเกิดขึ้น คือ 1, 2, 3, 4, 5 หรือ 6
ผลลัพธ์ที่อาจจะเกิดขึ้นจากการทดลองสุ่มกรณีใดกรณีหนึ่ง เรียกผลลัพธ์ในกรณีที่สนใจจากการทดลองสุ่มนั้นว่า เหตุการณ์
ในการทดลองสุ่มนี้สามารถนำไปใช้ในการช่วยเลือกตัดสินใจกระทำสิ่งใดสิ่งหนึ่ง เพื่อให้เกิดผลที่พึงพอใจต่อตนเองมากที่สุด
เหตุการณ์บางเหตุการณ์ไม่เป็นการทดลองสุ่ม เพราะเกิดเพียงเหตุการณ์เดียวหรือทราบผลที่เกิดขึ้นอย่างแน่นอนแล้ว เช่น
-
- ในเอเชียพระอาทิตย์ขึ้นทางทิศตะวันออก
- นิ้งหยิบได้ลูกแก้วสีขาวจากกล่องที่มีลูกแก้วสีขาวบรรจุอยู่ 3 ลูก
- น้ำหนึ่งเลือกซื้อรถจักรยานสีแดงตามที่ตัวเองชอบ
เหตุการณ์
เหตุการณ์ หมายถึง ผลลัพธ์ที่เราสนใจจากผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้จากการทดลองสุ่ม
ตัวอย่างที่ 1 จากการทดลองทอดลูกเต๋า 2 ลูกพร้อมกัน 1 ครั้ง จงตอบคำถามต่อไปนี้
1) ผลรวมของแต้มลูกเต๋าเป็น 7
2) ผลของการทอดลูกเต๋าครั้งแรกเป็น 1
3) เหตุการณ์ที่จะได้แต้มเหมือนกัน
วิธีทำ ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการทอดลูกเต๋า 2 ลูกพร้อมกัน 1 ครั้ง คือ
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
1) ผลรวมของแต้มลูกเต๋าเป็น 7
ผลลัพธ์ที่เราสนใจนั้น ได้แก่ (1, 6), (2, 5), (3, 4), (4, 3), (5, 2) และ (6, 1)
2) ผลของการทอดลูกเต๋าครั้งแรกเป็น 1
ผลลัพธ์ที่เราสนใจนั้น ได้แก่ (1, 1), (1, 2), (1, 3), (1, 4), (1, 5) และ (1, 6)
3) เหตุการณ์ที่จะได้แต้มเหมือนกัน
ผลลัพธ์ที่เราสนใจนั้น ได้แก่ (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) และ (6, 6)
ตัวอย่างที่ 2 โยนเหรียญบาท 3 เหรียญ 1 ครั้ง พร้อมกัน จงหาผลลัพธ์ของเหตุการณ์ต่อไปนี้
1) เหตุการณ์ที่จะออกหัว 2 เหรียญ
2) เหตุการณ์ที่จะออกหัวอย่างน้อย 1 เหรียญ
3) เหตุการณ์ที่จะออกก้อยอย่างน้อย 2 เหรียญ
4) เหตุการณ์ที่จะออกหัวทั้ง 3 เหรียญ หรือได้ก้อยทั้ง 3 เหรียญ
วิธีทำ ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการโยนเหรียญบาท 3 เหรียญ 1 ครั้ง พร้อมกัน อาจใช้แผนภาพต้นไม้ ดังนี้
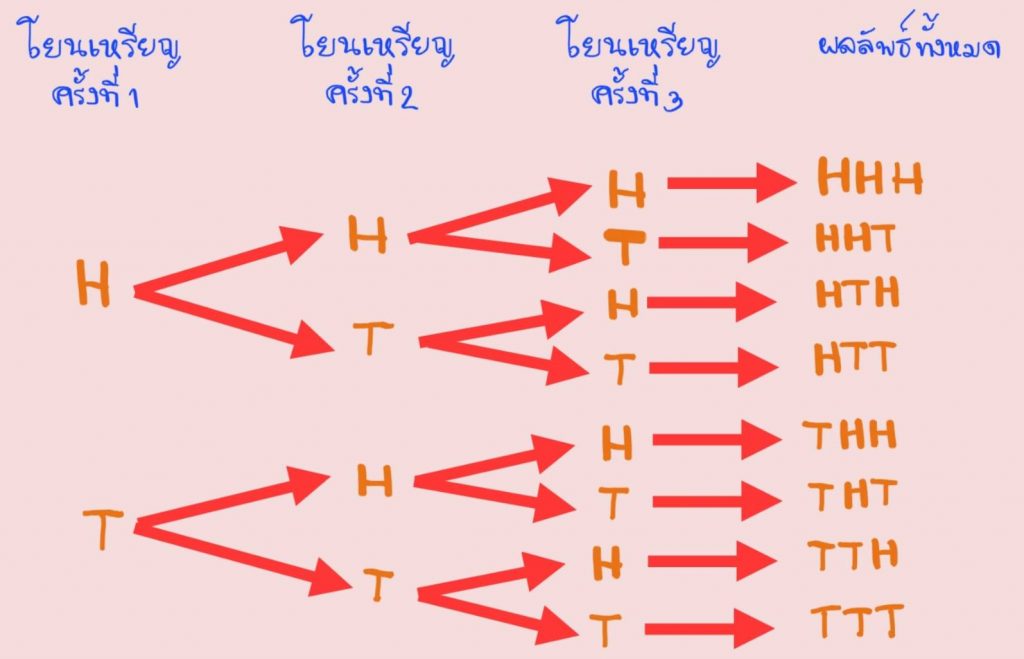
จะได้ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มมี 8 แบบ คือ HHH, HHT, HTH, HTT, THH, THT, TTH หรือ TTT
1) เหตุการณ์ที่จะออกหัว 2 เหรียญ มีผลลัพธ์ 3 แบบ คือ HHT, HTH, และ THH
2) เหตุการณ์ที่จะออกหัวอย่างน้อย 1 เหรียญ มีผลลัพธ์ 7 แบบ คือ HHH, HHT, HTH, HTT, THH, THT และ TTH
3) เหตุการณ์ที่จะออกก้อยอย่างน้อย 2 เหรียญ มีผลลัพธ์ 4 แบบ คือ HTT, THT, TTH และ TTT
4) เหตุการณ์ที่จะออกหัวทั้ง 3 เหรียญ หรือได้ก้อยทั้ง 3 เหรียญ มีผลลัพธ์ 2 แบบ คือ HHH และ TTT
ตัวอย่างที่ 3 สุ่มหยิบสลาก 2 ใบ จากในกล่องที่บรรจุสลาก 3 ใบ ซึ่งมีหมาย 1, 2 และ 3 ตามลำดับ จงหาผลลัพธ์ของเหตุการณ์ที่จะได้ผลบวกของสลากสองใบเท่ากับ 5 เมื่อกำหนดการทดลองสุ่มดังนี้
1) หยิบสลาก 2 ใบ พร้อมกัน
2) หยิบสลากทีละใบโดยไม่ใส่คืนก่อนจะหยิบสลากใบที่สอง
3) หยิบสลากทีละใบโดยใส่คืนก่อนจะหยิบสลากใบที่สอง
วิธีทำ 1) หยิบสลาก 2 ใบ พร้อมกัน จะได้ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มมี 3 แบบ คือ (1, 2), (1, 3) หรือ (2, 3)
เหตุการณ์ที่ผลบวกของสลากทั้งสองใบเท่ากับ 5 มี 1 แบบ คือ (2, 3)
2) หยิบสลากทีละใบโดยไม่ใส่คืนก่อนจะหยิบสลากใบที่สอง จะได้ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มมี 6 แบบ คือ (1, 2), (1, 3), (2, 1), (2, 3), (3, 1) หรือ (3, 2)
เหตุการณ์ที่ผลบวกของสลากทั้งสองใบเท่ากับ 5 มี 2 แบบ คือ (2, 3) และ (3, 2)
3) หยิบสลากทีละใบโดยใส่คืนก่อนจะหยิบสลากใบที่สอง จะได้ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มมี 9 แบบ คือ (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2) หรือ (3, 3)
เหตุการณ์ที่ผลบวกของสลากทั้งสองใบเท่ากับ 5 มี 2 แบบ คือ (2, 3) และ (3, 2)
ตัวอย่างที่ 4 กล่องใบหนึ่งมีสลากอยู่ 4 ใบ แต่ละใบเขียน A, B, C และ D กำกับไว้ จงหาผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้ตามเงื่อนไขต่อไปนี้
1) สุ่มหยิบ 2 ใบพร้อมกัน
2) สุ่มหยิบ 3 ใบพร้อมกัน
วิธีทำ 1) สุ่มหยิบ 2 ใบพร้อมกัน เนื่องจาก การสุ่มหยิบ 2 ใบ พร้อมกันนั้นไม่สนใจลำดับของการหยิบ
ดังนั้น ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการสุ่มหยิบสลาก 2 ใบ พร้อมกัน ได้แก่ AB, AC, AD, BC, BD และ CD
2) สุ่มหยิบ 3 ใบพร้อมกัน เนื่องจาก การสุ่มหยิบ 3 ใบ พร้อมกันนั้นไม่สนใจลำดับของการหยิบเช่นกัน
ดังนั้น ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการสุ่มหยิบสลาก 3 ใบ พร้อมกัน ได้แก่ ABC, ABD, ACD และ BCD
ตัวอย่างที่ 5 สุ่มหยิบสลาก 1 ใบ จากสลาก 5 ใบ ที่มีตัวอักษร A, E, I, O และ U กำกับใบละหนึ่งตัว
1) ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้จากการทดลองนี้
2) เหตุการณ์ที่หยิบได้สลากที่เป็นพยัญชนะ
วิธีทำ 1) ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้จากการทดลองนี้ ได้แก่ เหตุการณ์ที่หยิบได้สลากที่เป็นสระ ได้แก่ A, E, I, O หรือ U
2) เหตุการณ์ที่หยิบได้สลากที่เป็นพยัญชนะ ไม่มี
ตัวอย่างที่ 6 มีอมยิ้มอยู่ 3 สี สีละ 1 ลูก คือ สีเหลือง สีส้ม และสีเขียว ใส่อมยิ้มทั้งหมดลงในกล่อง แล้วสุ่มหยิบอมยิ้ม 2 ลูก จงหาผลลัพธ์ของเหตุการณ์ที่จะหยิบได้อมยิ้มสีเดียวกัน เมื่อกำหนดการทดลองสุ่มดังนี้
1) หยิบอมยิ้ม 2 ลูก พร้อมกันโดยไม่ดู
2) หยิบครั้งละ 1 ลูก โดยไม่ใส่คืน
วิธีทำ กำหนดให้ ล แทน อมยิ้มสีเหลือง
ส แทน อมยิ้มสีส้ม
ข แทน อมยิ้มสีเขียว
1) หยิบอมยิ้ม 2 ลูก พร้อมกันโดยไม่ดู
ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มมี 3 แบบ คือ (ส, ล), (ข, ล) และ (ข, ส)
เหตุการณ์ที่จะหยิบได้อมยิ้มสีเดียวกันไม่สามารถเกิดขึ้นได้ เนื่องจากอมยิ้มมีอยู่ 3 สี สีละ 1 ลูก ไม่สามารถหยิบได้อมยิ้มสีเดียวกัน 2 ลูก ได้
2) หยิบครั้งละ 1 ลูก โดยไม่ใส่คืน
ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นจากการทดลองสุ่มมี 6 แบบ คือ (ล, ส), (ล, ข), (ส, ล), (ส, ข), (ข, ล) และ (ข, ส)
เหตุการณ์ที่จะหยิบได้อมยิ้มสีเดียวกันไม่สามารถเกิดขึ้นได้ เนื่องจากอมยิ้มมีอยู่ 3 สี สีละ 1 ลูก ไม่สามารถหยิบได้อมยิ้มสีเดียวกัน 2 ลูก ได้
เมื่อน้องๆเรียนรู้เรื่อง การทดลองสุ่มและเหตุการณ์ จะทำให้น้องๆ สามารถเข้าใจการทดลองสุ่มและเหตุการณ์ เพื่อสามารถนำมาคำนวณหาความน่าจะเป็นของเหตุการณ์ได้ในลำดับถัดไป ได้อย่างถูกต้องและแม่นยำ และสามารถนำความรู้ที่ได้ไปประกอบในการตัดสินใจเรื่องต่างๆ ในอนาคตได้



















