การบวก ลบ และคูณเมทริกซ์
การบวก ลบ และคูณเมทริกซ์ เราจะนำสมาชิกของเมทริกซ์แต่ละเมทริกซ์มาบวก ลบ คูณกัน ซึ่งการดำเนินการเหล่านี้มีสมบัติและข้อยกเว้นต่างกันไป เช่น การบวกต้องเอาสมาชิกตำแหน่งเดียวกันมาบวกกัน เป็นต้น
ต่อไปเราจะมาดูวิธีการบวก ลบ และคูณเมทริกซ์กันค่ะ
การบวกเมทริกซ์
เมทริกซ์ที่จะนำมาบวกกันได้นั้น ต้องมีมิติเท่ากัน และการบวกจะนำสมาชิกตำแหน่งเดียวกันมาบวกกัน
เช่น
1.)
2.)
การลบเมทริกซ์
การลบเมทริกซ์จะคล้ายๆกับการบวกเมทริกซ์เลย คือ มิติของเมทริกซ์ที่จะนำมาบวกกันจะต้องเท่ากัน แต่ต่างกันตรงที่สมาชิกข้างในเมทริกซ์จะต้องนำมาลบกัน เช่น
1.)
2.)
สมบัติการบวกเมทริกซ์
- สมบัติปิดการบวก คือ เมทริกซ์ที่มีมิติเดียวกันบวกกันแล้วผลลัพธ์ยังเป็นเมทริกซ์เหมือนเดิมและมิติก็เท่าเดิมด้วย
- สมบัติการสลับที่การบวก คือ ให้ A และ B เป็นเมทริกซ์ จะได้ว่า A +B = B +A
- สมบัติการเปลี่ยนหมู่ คือ (A + B) + C = A + (B + C)
- สมบัติการมีเอกลักษณ์การบวก ซึ่งเอกลักษณ์การบวกของเมทริกซ์ คือ เมทริกซ์ศูนย์ (สมาชิกทุกตำแหน่งเป็น 0) เขียนแทนด้วย
- สมบัติการมีตัวผกผัน คือ ถ้า A เป็นเมทริกซ์ใดๆแล้วจะได้ว่า (-A) เป็นเมทริกซ์ผกผันของ A ซึ่งเมื่อนำ A มาบวกกับ -A แล้วจะได้เมทริกซ์ศูนย์
การคูณเมทริกซ์ ด้วยจำนวนจริง
การคูณเมทริกซ์ด้วยจำนวนจริงคือ การนำจำนวนจริงค่าหนึ่งคูณกับเมทริกซ์ ซึ่งวิธีการคูณแบบนี้น้องๆสามารถนำจำนวนจริงนั้นเข้าไปคูณกับสมาชิกในตำแหน่งในเมทริกซ์ (ต้องคูณทุกตัวแหน่ง) และเมทริกซ์นั้นจะเป็นกี่มิติก็ได้ เช่น
สมบัติการคูณเมทริกซ์ด้วยจำนวนจริง
ให้ A, B เป็นเมทริกซ์ที่มีมิติ และ c, d เป็นจำนวนจริง
- (cd)A = c(dA) = d(cA) เช่น
- c(A + B) = cA + cB
- (c + d)A = cA + dA
- 1(A) = A และ -1(A) = -A
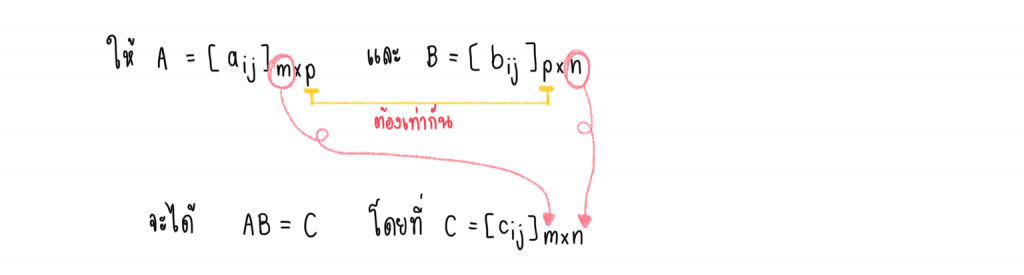
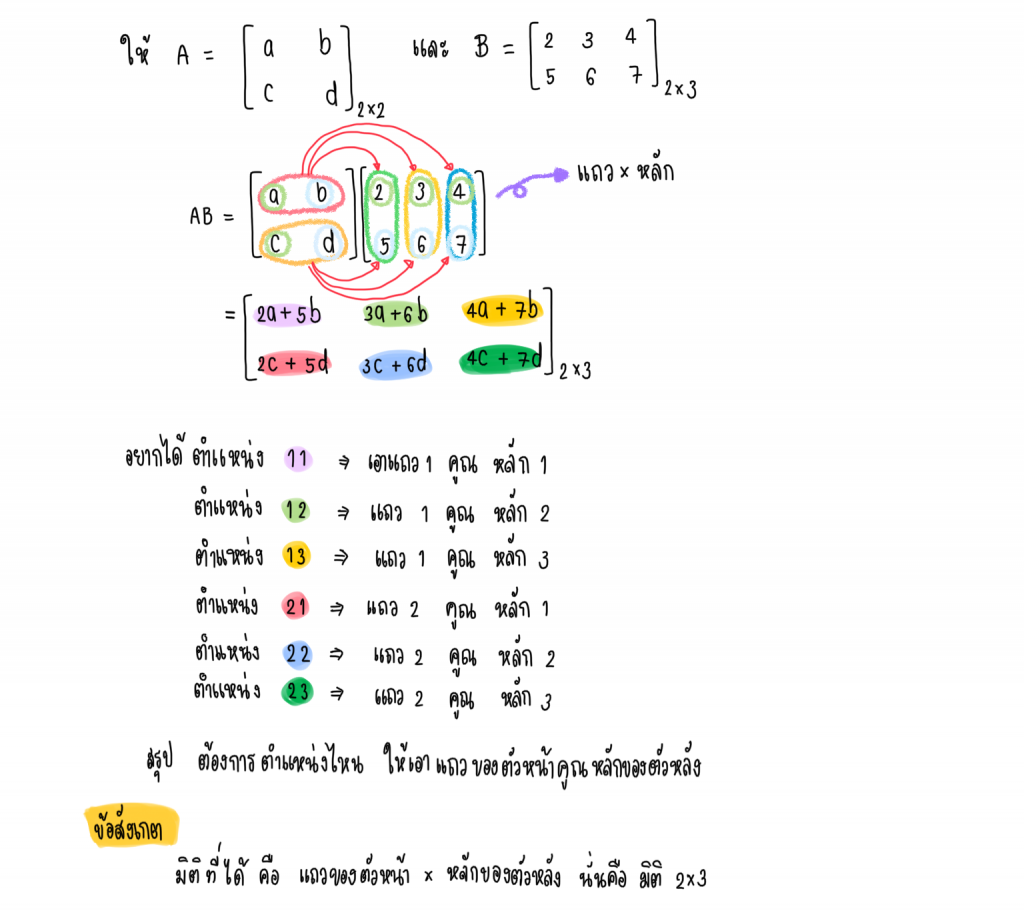
การคูณเมทริกซ์ด้วยเมทริกซ์
เมทริกซ์ที่จะคูณกันได้ต้องมีหลักเกณฑ์ดังนี้
1.) จำนวนหลักของเมทริกซ์ตัวหน้าต้อง เท่ากับ จำนวนแถวของเมทริกซ์ตัวหลัง
2.) มิติของเมทริกซ์ผลลัพธ์จะเท่ากับ จำนวนแถวของตัวหน้าคูณจำนวนหลักของตัวหลัง
เช่น
วิธีการคูณเมทริกซ์
สมบัติการคูณเมทริกซ์ด้วยเมทริกซ์
1.) สมบัติการเปลี่ยนหมู่
ถ้า A, B และ C เป็นเมทริกซ์ที่สามารถคูณติดต่อกันได้ จะได้ A(BC) = (AB)C
2.) สมบัติการมีเอกลักษณ์
เอกลักษณ์การคูณของเมทริกซ์ คือ
น้องๆสามารถทำความรู้จักกับเมทริกซ์เอกลักษณ์เพิ่มเติม ได้ที่ >>> เมทริกซ์เอกลักษณ์
**เมทริกซ์ที่มีเอกลักษณ์ คือ เมทริกซ์จัตุรัส
3.) สมบัติการรแจกแจง
(A + B)C = AC + BC
A(B +C) = AB + AC
แต่!! เมทริกซ์จะมีสมบัติการแจกแจง เมื่อ A + B, B + C, AB, AC, BC สามารถหาค่าได้
สิ่งที่น้องๆต้องรู้เกี่ยวกับการคูณเมทริกซ์ด้วยเมทริกซ์
1.) ไม่มีสมบัติการสลับที่การคูณ นั่นคือ AB ไม่จำเป็นต้องเท่ากับ BA เช่น

2.) เมื่อ AB = BA จะได้
3.) ถ้า ไม่จำเป็นที่
หรือ
4.) ถ้า โดยที่
ไม่จำเป็นที่