ฟังก์ชันลอการิทึม

ฟังก์ชันลอการิทึม คือฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียล จากที่ฟังก์ชันเอกซ์โพเนนเชียลคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์ที่ส่งจากจำนวนจริงไปยังจำนวนจริงบวก โดยที่ ดังนั้นฟังก์ชันดังกล่าวซึ่งเป็นฟังก์ชันผกผันของเอกซ์โพเนนเชียล ก็คือ คู่อันดับ (y, x)  หรืออาจจะบอกได้อีกแบบคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์จากจำนวนจริงบวกไปยังจำนวนจริง โดยที่ จัดรูปใหม่ ได้เป็น (อ่านว่าล็อก x ฐาน a)

บทนิยาม

logarithm คือฟังก์ชันที่อยู่ในรูป {(x, y) ∈ : } โดยที่ a เป็นจำนวนจริงที่มากกว่า 0 และ a ≠ 1

ตัวอย่าง 

จัดรูปเป็น อ่านว่า ล็อก x ฐาน 5

กราฟ

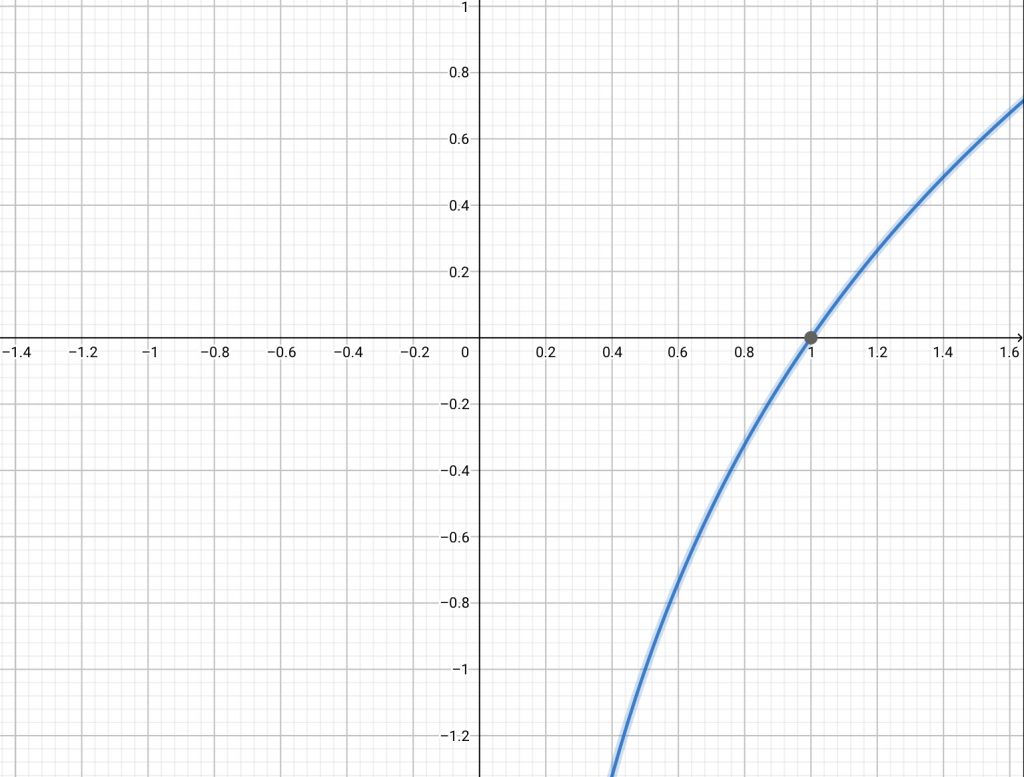
กรณี a > 1

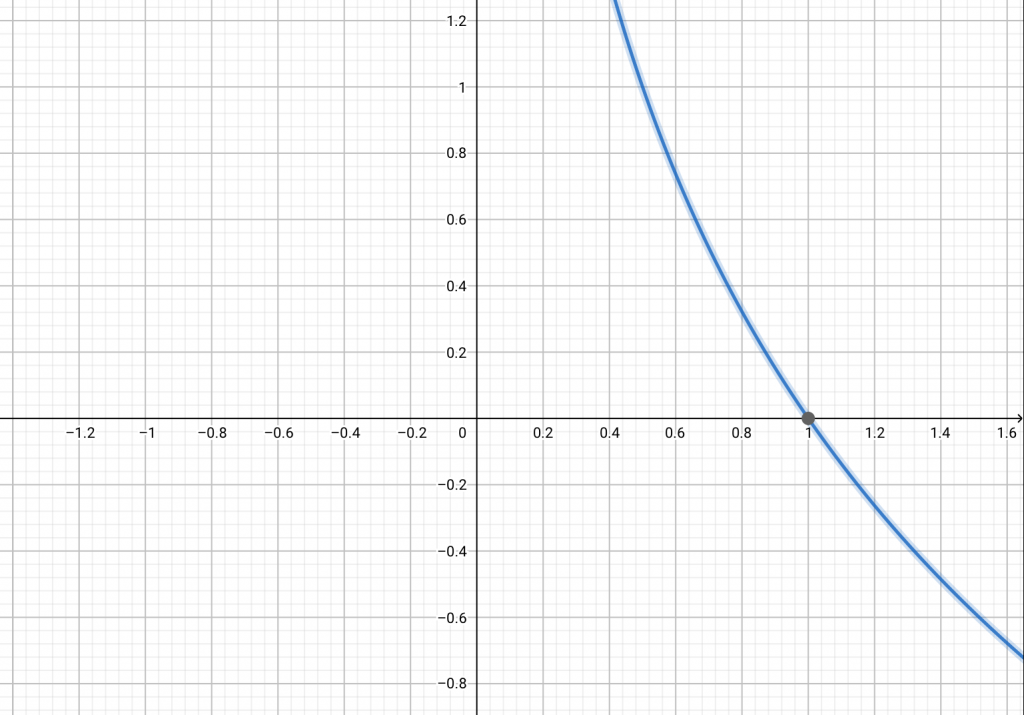
กรณี 0 < a < 1

จากกราฟจะเห็นว่า

1.) เมื่อ a > 1 จะเป็นฟังก์ชันเพิ่ม

2.) เมื่อ 0 < a < 1 จะเป็นฟังก์ชันลด

3.) กราฟของทั้ง 2 กรณีจะไม่ตัดแกน y

4.) ค่า x จะเป็นบวกเสมอ แต่ค่า y เป็นได้ทั้งบวกและลบ

สมบัติ ฟังก์ชันลอการิทึม

ให้ a, M และ N เป็นจำนวนจริงบวกที่ a ≠ 1 และ k เป็นจำนวนจริง จะได้ว่า

1.)

(ล็อกผลคูณเท่ากับผลบวกของล็อก)

2.)

(ล็อกผลหารเท่ากับผลต่างของล็อก)

3.)

เช่น   

4.)

5.)

(ล็อก 1 เท่ากับ 0)

6.)   เมื่อ k ≠ 0

เช่น 

7.)   เมื่อ b >0 และ b ≠ 1

เช่น 

8.)   เมื่อ N ≠ 1

เช่น      (เลขฐานไม่จำเป็นต้องเป็นเลข 2 เป็นเลขอะไรก็ได้ที่มากกว่า 0 และไม่เท่ากับ 1 )

การหาค่าลอการึทึม

ลอการิทึมที่ใช้มากและค่อนข้างนิยมใช้ในการคำนวณ คือ ลอการิทึมสามัญ (common logarithm) ซึ่งก็คือลอการิทึมที่มีเลขฐานสิบ และโดยทั่วไปเราจะเขียนล็อกโดยไม่มีฐานกำกับ

เช่น

จากสมบัติข้อที่ 3 และ 4 จะได้ว่า

ดังนั้น จะได้ว่า   เมื่อ n เป็นจำนวนเต็มใดๆ

ดังนั้น ถ้า N เป็นจำนวนเต็มบวกใดๆ เราสามารถเขียนอยู่ในรูป ได้เสมอ โดยที่ 0 ≤ N < 10

เช่น ,

ทีนี้เรามาพิจารณา

เมื่อ 0 ≤ N < 10

จะได้ว่า

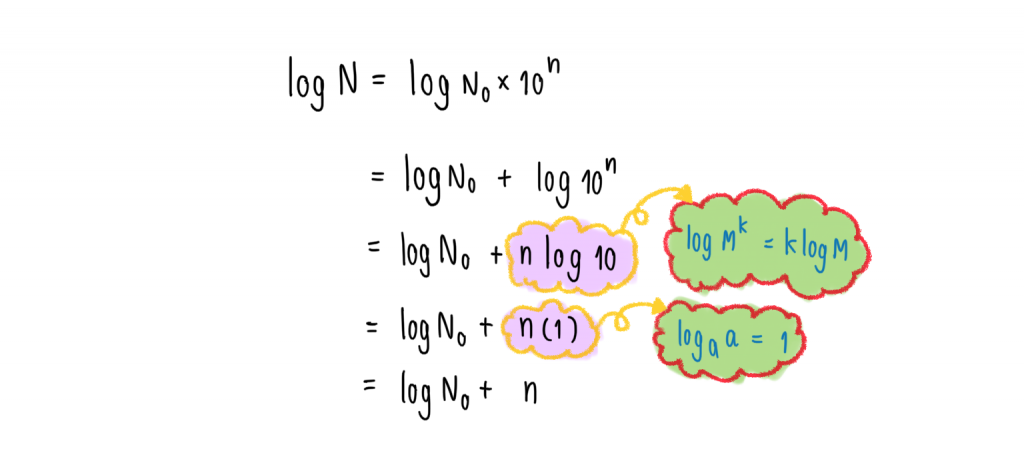
เราจะเรียก   ว่า แมนทิสซาของ

และเรียก n ว่า แคแรกเทอริสติกของ 

บทนิยาม

1. ถ้า log N = A จะเรียก N ว่า แอนติลอการิทึมของ log N
2. ถ้า log N = A จะได้ว่า N = antilog A

ตัวอย่าง

ให้หาค่าแคแรกเทอริสติกของ log 56.2

ลอการิทึมที่นิยมใช้และมีประโยชน์มากเมื่อเรียนคณิตศาสตร์ขั้นที่สูงขึ้น คือ ลอการิทึมฐาน e โดยที่ e คือสัญลักษณ์ค่าคงที่ ซึ่ง e ≈ 2.7182818 ซึ่งล็อกฐาน e เราจะเรียกอีกอย่างว่า ลอการิทึมธรรมชาติ มักจะเขียนอยู่ในรูป ln x (อ่านว่าล็อก x ฐาน e)

การเปลี่ยนฐานของลอการิทึม

ตัวอย่างการเปลี่ยนฐานของลอการิทึม

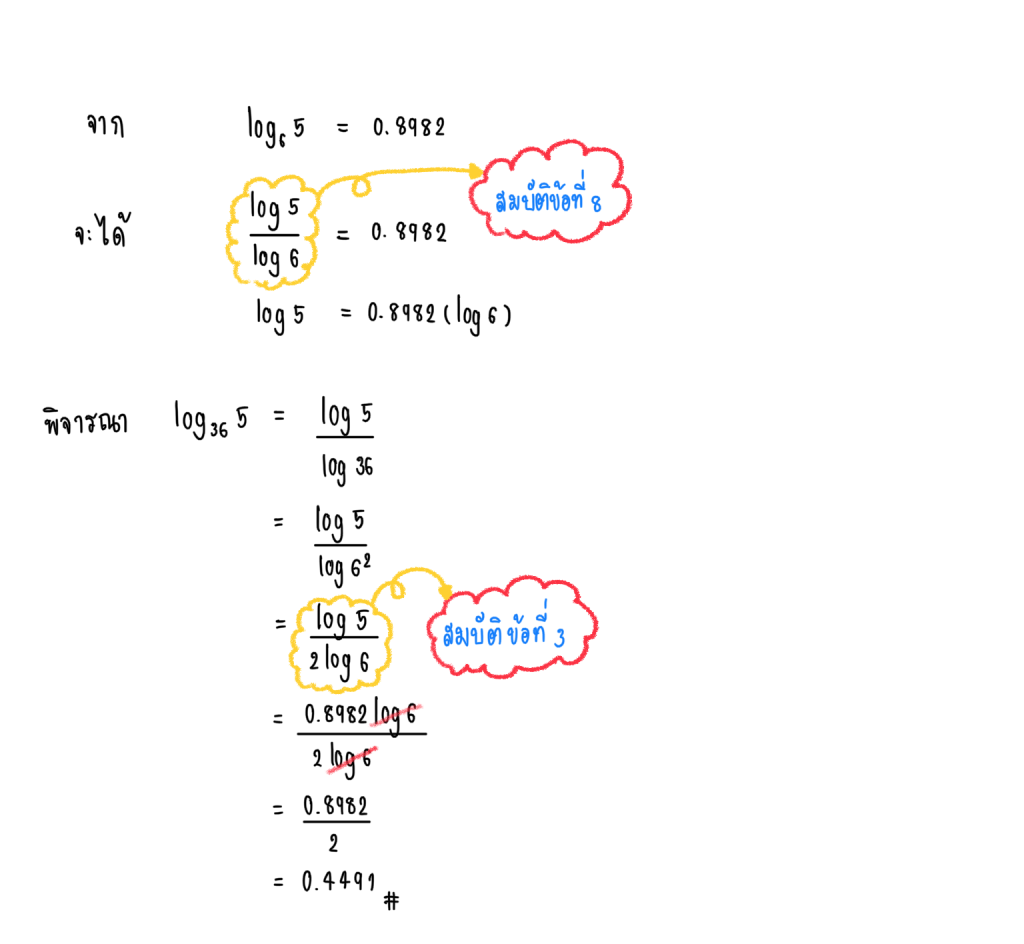
กำหนดให้ จงหาค่า

น้องๆสามารถเข้าไปอ่านบทความ ฟังก์ชันเอกซ์โพเนนเชียล เพื่อจะได้เข้าใจกับฟังก์ชันลอการิทึมง่ายขึ้น