ทศนิยมมีค่าประจำหลักเป็นเศษส่วน ซึ่งเมื่อนำทศนิยมคูณด้วยทศนิยมผลลัพธ์ที่ได้ออกจะมีจะตำแหน่งของทศนิยมที่เปลี่ยนไป ตามหลักการคูณทศนิยมที่กล่าวไว้ดังนี้ “จำนวนตำแหน่งของทศนิยมของผลคูณต้องเท่ากับตำแหน่งของทศนิยมของตั้วตั้งและตัวคูณรวมกัน”

รูปแบบการคูณทศนิยม มีทั้งหมด 2 รูปแบบ

1.การคูณทศนิยมกับจำนวนเต็ม

หลักการคูณทศนิยมกับจำนวนเต็มนั้นสามารถทำได้ 2 วิธี

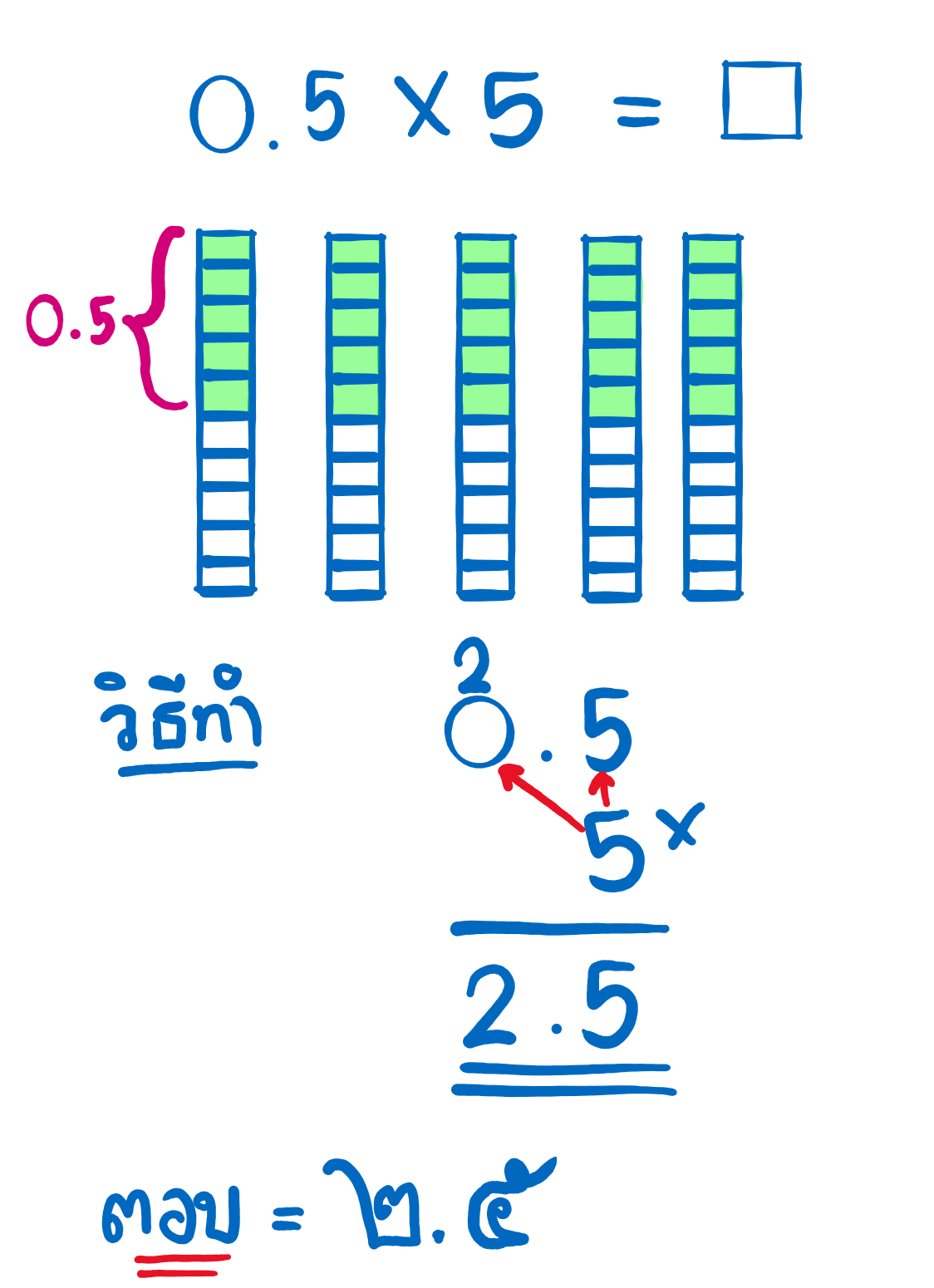
1.1 วิธีตั้งคูณ

สิ่งสำคัญของการตั้งคูณคือ ต้องว่างจุดทศนิยมที่ตำแหน่งเดิมและทำการคูณตัวเลขตามหลักการคูณของจำนวนเต็มปกติ

1.2 วิธีแปลงทศนิยมให้เป็นเศษส่วน

วิธีนี้ใช้หลักการคูณเศษส่วนในการคำนวณ โดยเมื่อทำทศนิยมให้เป็นเศษส่วนแล้ว ต้องทำให้จำนวนเต็มเป็นเศษส่วนด้วย ซึ่งตัวส่วนของจำนวนเต็มจะมีค่าเป็น 1 เสมอ จากนั้นก็ทำการคูณโดยนำตัวเศษคูณด้วยตัวเศษ และตัวส่วนคูณด้วยตัวส่วน เมื่อได้ผลลัพธ์แล้วต้องแปลงกลับเป็นเป็นทศนิยมอีกครั้ง

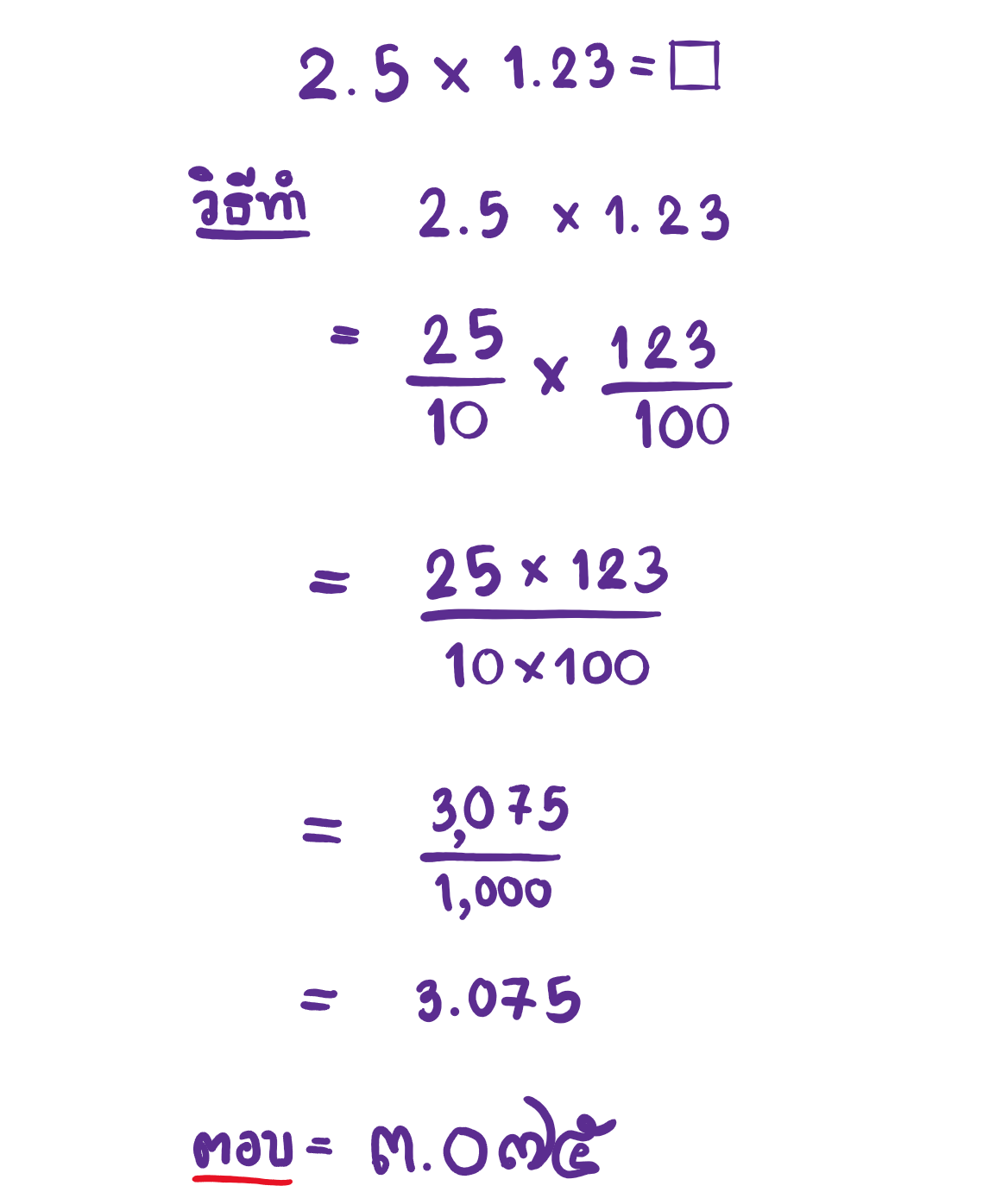
2.การคูณทศนิยมกับทศนิยม

หลักการคูณทศนิยมกับทศนิยมนั้นสามารถทำได้ 2 วิธี

2.1 วิธีตั้งคูณ

• ตัวตั้งเป็นทศนิยม 1 ตำแหน่งและตัวคูณเป็นทศนิยม 1 ตำแหน่ง รวมเป็นทศนิยม 2 ตำแหน่ง ดังนั้นผลคูณที่ได้จะต้องตอบเป็นทศนิยม 2 ตำแหน่ง
• ตัวตั้งเป็นทศนิยม 2 ตำแหน่งและตัวคูณเป็นทศนิยม 1 ตำแหน่ง รวมเป็นทศนิยม 3 ตำแหน่ง ดังนั้นผลคูณที่ได้จะต้องตอบเป็นทศนิยม 3 ตำแหน่ง แต่จะมีบางกรณีที่ผลคูณมีตัวเลข 0 เป็นเลขสุดท้าย จะทำให้ตำแหน่งของทศนิยมลดลงได้
• ตัวตั้งเป็นทศนิยม 3 ตำแหน่งและตัวคูณเป็นทศนิยม 2 ตำแหน่ง รวมเป็นทศนิยม 5 ตำแหน่ง ดังนั้นผลคูณที่ได้จะต้องตอบเป็นทศนิยม 5 ตำแหน่ง แต่จะมีบางกรณีที่ผลลัพธ์ที่ได้อาจจะไม่ถึง 5 ตัวเลข ต้องทำการเติมเลข 0 ข้างหน้าผลลัพธ์ เพื่อทำให้ครบ 5 ตำแหน่ง

2.2 วิธีแปลงทศนิยมให้เป็นเศษส่วน

วิธีนี้ใช้หลักการคูณเศษส่วนในการคำนวณ โดยเมื่อทำทศนิยมของตัวตั้ง และตัวคูณให้เป็นเศษส่วนแล้ว จากนั้นก็ทำการคูณโดยนำตัวเศษคูณด้วยตัวเศษ และตัวส่วนคูณด้วยตัวส่วน เมื่อได้ผลลัพธ์แล้วต้องแปลงกลับเป็นเป็นทศนิยมอีกครั้ง โดยตำแหน่งของทศนิยมสามารถดูจากจำนวน 0 ที่เป็นผลลัพธ์ของการคูณตัวส่วน

คลิปตัวอย่างการคูณทศนิยม