ยอดนิยม!

เตรียมสอบเข้า ม.1 โรงเรียนสวนกุหลาบวิทยาลัย
เตรียมสอบเข้าม.1 โรงเรียนสวนกุหลาบวิทยาลัย สวัสดีค่ะน้อง ๆ วันนี้มาพบกับพี่แอดมินและ Nock Academy อีกเช่นเคย ซึ่งเรายังคงอยู่กับหัวข้อของการเตรียมสอบเข้าม.1กันนะคะ วันนี้แอดมินจะพาน้อง ๆ ไปรู้จักกับโรงเรียนสวนกุหลาบวิทยาและการเตรียมตัวสอบเข้าในระดับชั้นม.1ของโรงเรียนแห่งนี้กันค่ะ ก่อนอื่นแอดมินต้องขอกล่าวประวัติคร่าว ๆ ของโรงเรียนให้ทุกคนได้รู้จักกันก่อนนะคะ โรงเรียนสวนกุหลาบวิทยาเป็นโรงเรียนชายล้วนที่ก่อตั้งขึ้นมาในสมัยพระบาทสมเด็จพระจุลจอมเกล้าเจ้าอยู่หัว (รัชกาลที่ 5) ถือเป็นโรงเรียนรัฐบาลแห่งแรกของประเทศไทย ที่มีความโดดเด่นในเรื่องของวิชาการ ภาษาและความเป็นผู้นำ โดยศิษย์เก่าที่สำเร็จการศึกษามาจากโรงเรียนสวนกุหลาบวิทยาลัยแห่งนี้หลายคนเป็นผู้ที่มีชื่อเสียงและประสบความเร็จจึงทำให้ชื่อเสียงของโรงเรียนสวนกุหลาบวิทยาลัยนั้นเป็นที่รู้จักกันอย่างแพร่หลายในสังคมไทยมาอย่างยาวนาน หลักสูตรสวนกุหลาบวิทยาลัย ม.ต้น ในปัจจุบันโรงเรียนสวนกุหลาบวิทยาลัยได้มีการปรังปรุงและพัฒนาหลักสูตรให้มีความเท่าทันสังคมไทยในปัจจุบันมากยิ่งขึ้น

มารู้จักกับการถามทางในภาษาอังกฤษ Asking for Direction in English
สวัสดีค่ะนักเรียนป.5 ที่น่ารักทุกคน เคยมั้ยที่เราเจอฝรั่งถามทางแล้วตอบไม่ได้ ทำได้แค่ชี้ๆ แล้วก็บ๊ายบาย หากทุกคนเคยเจอปัญหานี้ ต้องท่องศัพท์และรู้โครงสร้างประโยคที่สำคัญในการถามทางแล้วล่ะ หากพร้อมแล้วก็ไปลุยกันเลย มารู้จักกับการถามทางในภาษาอังกฤษ Asking for Direction in English การถามทิศทางจะต้องมีประโยคเกริ่นก่อนเพื่อให้คนที่เราถาม ตั้งตัวได้ว่า กำลังจะโดนถามอะไร ยังไง ซึ่งเราสามารถถามได้ทั้ง คำถามแบบสุภาพเมื่อพูดกับคนที่เราไม่คุ้นเคย หรือ คำถามทั่วไปเมื่อพูดกับคนใกล้ตัว

สำนวนไทยที่เราควรรู้ และตัวอย่างการนำไปใช้ในชีวิตประจำวัน
น้อง ๆ เคยเป็นกันหรือเปล่าคะ เวลาที่อยากจะพูดอะไรสักอย่างแต่มันช่างยาวเหลือเกิน กว่าจะพูดออกมาหมดนอกจากคนฟังจะเบื่อแล้วยังอาจทำให้เขาไม่สนใจคำพูดของเราเลยก็เป็นไปได้ เพราะอย่างนั้นแหละค่ะในภาษาไทยของเราจึงต้องมีสิ่งที่เรียกว่าสำนวนขึ้นมาเพื่อใช้บอกเล่าเรื่องราวที่ถูกกลั่นกรองออกมาจนได้คำที่สละสลวย รวมใจความยาว ๆ ให้สั้นลง ทำให้เราไม่ต้องพูดอะไรให้ยืดยาวอีกต่อไป บทเรียนในวันนี้จะพาน้อง ๆ ไปทบทวนความรู้เรื่อง สำนวนไทย รวมถึงตัวอย่างสำนวนน่ารู้ในชีวิตประจำวันเพิ่มเติมด้วยค่ะ จะมีอะไรบ้างนั้น ไปดูกันเลย ความหมายและลักษณะของ สำนวนไทย สำนวน หมายถึง ถ้อยคำหรือสำนวนพูดหรือเขียนที่มีความหมายไม่ตรงกับรากศัพท์หรือตรงไปตรงมาตามพจนานุกรม แต่เป็นถ้อยคำที่มีความหมายเป็นอย่างอื่น

ประโยคปฏิเสธรูปแบบอดีต
สวัสดีค่ะนักเรียน ม.2 ที่น่ารักทุกคน วันนี้ครูจะพาไปทบทวนเรื่อง ประโยคปฏิเสธรูปแบบอดีต ซึ่งเมื่อเล่าถึงเวลาในอดีตส่วนใหญ่แล้วเรามักเจอคำว่า yesterday (เมื่อวานนี้), 1998 (ปี ค.ศ. ที่ผ่านมานานแล้ว), last month (เดือนที่แล้ว) และกลุ่มคำอื่นๆ ที่กำกับเวลาในอดีต ซึ่งเราจะเจอ Past Time Expressions ในกลุ่ม Past Tenses หรือ อดีตกาล
บทความเตรียมสอบแนะนำ

เตรียมสอบเข้า ม.1 โรงเรียนสตรีวิทยา
เตรียมสอบเข้า ม.1 โรงเรียนสตรีวิทยากันเถอะ สวัสดีค่ะ มาพบกับแอดมินและ Nock Academy กับบทความเตรียมสอบเข้าม.1 กันอีกแล้วแต่วันนี้เรามาในบทความการสอบเข้าของโรงเรียนสตรีวิทยา โรงเรียนหญิงล้วนที่มีชื่อเสียงโด่งดังมานานกว่า 118 ปี อีกทั้งยังเคยเป็นสถานศึกษาของสมเด็จย่าและเคยได้รับเสด็จสมเด็จพระราชินีนาถเอลิซาเบธที่ 2 กล่าวได้ว่าเป็นโรงเรียนที่มีความผูกพันธ์กับราชวงศ์ของไทยและเป็นสถานที่ที่เคยต้อนรับราชวงศ์ชั้นสูงมาแล้วอีกด้วย นับเป็นความภาคภูมิใจแก่ผู้ที่ได้เข้าศึกษาที่โรงเรียนแห่งนี้เป็นอย่างมาก ไม่เพียงแต่เรื่องของความเก่าแก่และยาวนานของโรงเรียนที่ทำให้โรงเรียนสตรีวิทยานั้นเป็นที่รู้จัก แต่ในด้านของวิชาการก็มีความเข้มข้นและการแข่งขันที่สูงด้วยเช่นเดียวกัน โรงเรียนสตรีวิทยาในปัจจุบันมีการเรียนการสอนตั้งแต่ระดับชั้นมัธยมศึกษาปีที่ 1 ไปจนถึงมัธยมศึกษาปีที่ 6 ถือได้ว่าเป็นโรงเรียนมัธยมขนาดใหญ่ มีอัตราการสอบเข้าศึกษาที่สูงมากในแต่ละปี

เตรียมสอบเข้า ม.1 โรงเรียนสวนกุหลาบวิทยาลัย
เตรียมสอบเข้าม.1 โรงเรียนสวนกุหลาบวิทยาลัย สวัสดีค่ะน้อง ๆ วันนี้มาพบกับพี่แอดมินและ Nock Academy อีกเช่นเคย ซึ่งเรายังคงอยู่กับหัวข้อของการเตรียมสอบเข้าม.1กันนะคะ วันนี้แอดมินจะพาน้อง ๆ ไปรู้จักกับโรงเรียนสวนกุหลาบวิทยาและการเตรียมตัวสอบเข้าในระดับชั้นม.1ของโรงเรียนแห่งนี้กันค่ะ ก่อนอื่นแอดมินต้องขอกล่าวประวัติคร่าว ๆ ของโรงเรียนให้ทุกคนได้รู้จักกันก่อนนะคะ โรงเรียนสวนกุหลาบวิทยาเป็นโรงเรียนชายล้วนที่ก่อตั้งขึ้นมาในสมัยพระบาทสมเด็จพระจุลจอมเกล้าเจ้าอยู่หัว (รัชกาลที่ 5) ถือเป็นโรงเรียนรัฐบาลแห่งแรกของประเทศไทย ที่มีความโดดเด่นในเรื่องของวิชาการ ภาษาและความเป็นผู้นำ โดยศิษย์เก่าที่สำเร็จการศึกษามาจากโรงเรียนสวนกุหลาบวิทยาลัยแห่งนี้หลายคนเป็นผู้ที่มีชื่อเสียงและประสบความเร็จจึงทำให้ชื่อเสียงของโรงเรียนสวนกุหลาบวิทยาลัยนั้นเป็นที่รู้จักกันอย่างแพร่หลายในสังคมไทยมาอย่างยาวนาน หลักสูตรสวนกุหลาบวิทยาลัย ม.ต้น ในปัจจุบันโรงเรียนสวนกุหลาบวิทยาลัยได้มีการปรังปรุงและพัฒนาหลักสูตรให้มีความเท่าทันสังคมไทยในปัจจุบันมากยิ่งขึ้น

เตรียมสอบเข้า ม.1 โรงเรียนสามเสนวิทยาลัย
มาเตรียมสอบเข้าสามเสนม.1 กันเถอะ เตรียมสอบเข้าสามเสนกันเถอะ! วันนี้ Nockacademy มีข้อมูลการสอบเข้าม.1 โรงเรียนสามเสนวิทยามาฝากกันค่า น้อง ๆ คนไหนกำลังหาข้อมูลอยู่ต้องกดบุ๊คมาร์คไว้แล้วเพราะว่าเรารวบรวมข้อมูลมาแบบจัดเต็ม ไปดูกันเลยดีกว่าว่าต้องเตรียมตัวยังไงบ้าง Let’s go! ก่อนอื่นต้องขอเกริ่นเกี่ยวกับโรงเรียนสามเสนวิทยาลัยก่อนเลยค่ะ ว่าทำไมโรงเรียนนี้ถึงเป็นที่มีชื่อเสียงมายาวนานแล้วก็มีอัตราการแข่งขันที่สูงมากที่สุดแห่งหนึ่ง เหตุผลก็เพราะว่าโรงเรียนสามเสนวิทยาลัยนั้นก่อตั้งมานานมากแล้วตั้งแต่ปีพ.ศ. 2494 มีการพัฒนาและยกระดับสถานศึกษามาอย่างต่อเนื่องจนถึงปัจจุบันก็ได้ขยายแผนการเรียนที่เฉพาะด้านมากยิ่งขึ้น จึงทำให้โรงเรียนสามารถผลิตนักเรียนที่มีความสามารถออกมาเป็นจำนวนมาก เด็ก ๆ จึงมีความต้องการที่จะสอบเข้าแข่งขันเพื่อเข้าศึกษาต่อกันอย่างล้นหลามนั้นเองค่ะ หลักสูตรสามเสนวิทยาลัยม.ต้น ก่อนอื่นต้องมาดูหลักสูตรกันก่อนเลยค่ะ ว่าหลักสูตรชั้นมัธยมศึกษาตอนต้นแบ่งออกเป็นอะไรบ้าง
บทความคณิตศาสตร์แนะนำ

ประมาณค่าทศนิยมด้วยการปัดทิ้งและปัดทด
บทความนี้จะพูดถึงเรื่องพื้นฐานของทศนิยมอีก 1 เรื่องก็คือการประมาณค่าใกล้เคียงของทศนิยม น้อง ๆคงอาจจะเคยเรียนการประมาณค่าใกล้เคียงของจำนวนเต็มมาแล้ว การประมาณค่าทศนิยมหลักการคล้ายกับการประมาณค่าจำนวนเต็มแต่อาจจะแตกต่างกันที่คำพูดที่ใช้ เช่นจำนวนเต็มจะใช้คำว่าหลักส่วนทศนิยมจะใช้คำว่าตำแหน่ง บทความนี้จึงจะมาแนะนำหลักการประมาณค่าทศนิยมให้น้อง ๆเข้าใจ และสามารถประมาณค่าทศนิยมได้อย่างถูกต้อง

สัดส่วน
บทความนี้ได้รวบรวมความรู้เรื่อง สัดส่วน รวมทั้งโจทย์ปัญหาเกี่ยวกับสัดส่วน ซึ่งได้รวบรวมเนื้อหาและเขียนอธิบายไว้อย่างชัดเจน รวมถึงมีคลิปวิดีโอการสอน เพื่ออำนวยความสะดวกให้กับน้องๆ สามารถเรียนรู้ได้ทุกที่ทุกเวลา แต่ก่อนจะเรียนรู้เรื่องสัดส่วนนั้น น้องๆจำเป็นต้องมีความรู้ในเรื่อง อัตราส่วนของจำนวนหลายๆจำนวน สามารถศึกษาเพิ่มเติมได้ที่ ⇒⇒ อัตราส่วนของจำนวนหลายๆจำนวน ⇐⇐ สัดส่วน สัดส่วน คือ ประโยคที่แสดงการเท่ากันของอัตราส่วนสองอัตราส่วน อัตราส่วนทั้งสองมีความสัมพันธ์ไปในทิศทางเดียวกันหรือในทิศทางตรงกันข้ามก็ได้ ชนิดของสัดส่วน สัดส่วนมี 2 ชนิด คือ สัดส่วนตรง และ สัดส่วนผกผัน

การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่ง
การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่ง การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่ง คือ การนำเสนอข้อมูลที่ได้มีการเก็บรวบรวมข้อมูลไว้โดยใช้รูปสี่เหลี่ยมมุมฉาก ซึ่งเเต่ละรูปมีความกว้างเท่ากัน เเละใช้ความสูงหรือความยาวเเสดงปริมาณของข้อมูล เเต่จุดเริ่มต้นจะต้องเริ่มในระดับเดียวกันเสมอ อาจอยู่ในเเนวตั้งหรือเเนวนอนก็ได้ การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่งเปรียบเทียบ คือ การนำเสนอข้อมูลโดยเปรียบเทียบข้อมูลตั้งเเต่ 2 ชุดขึ้นไปในแผนภูมิเดียวกัน โดยมีเเท่งสี่เหลี่ยมที่เเสดงข้อมูลชนิดเดียวกันอยู่ด้วยกันเป็นชุดๆ เเละมีสีหรือเเรเงาในเเท่งสี่เหลี่ยมต่างกัน เเละระบุไว้บนเเผนภูมิด้วยว่าสีหรือเเรเงานั้น ๆ เป็นข้อมูลของอะไร ตัวอย่างของแผนภูมิเเท่งเปรียบเทียบ ส่วนประกอบของเเผนภูมิแท่ง: 1. ชื่อแผนภูมิ 2. จำนวน 3.
บทความภาษาอังกฤษแนะนำ

Finite and Non- Finite Verb
Hi guys! สวัสดีค่ะนักเรียนชั้นม.6 ทุกคน วันนี้ครูจะพาไปทบทวนการใช้ “Finite and Non- Finite Verb” ในภาษาอังกฤษกันจร้า ถ้าพร้อมแล้วก็ไปลุยกันโลดจร้า คำเตือน: การเรียนเรื่องนี้จะทำให้นักเรียนมึนงงได้หากว่าพื้นฐานเรื่อง Part of speech, Subject , Tense, Voice และ Mood ของเราไม่แน่น
ประโยคความเดียวและประโยคความรวมในภาษาอังกฤษ
สวัสดีค่ะนักเรียนชั้นม.1 ที่น่ารักทุกคน เจอกันอีกแล้วจร้ากับไวยากรณ์การเขียนภาษาอังกฤษและวันนี้ครูจะพาไปดูเทคนิคการการใช้ประโยคความเดียว และประโยคความรวมในภาษาอังกฤษกันค่ะ ซึ่งเป็นไม้เบื่อไม้เมามากกับคนที่ไม่ชอบเขียน ครูเอาใจช่วยทุกคนค่า ไปลุยกันเลย 3 โครงสร้างประโยคในภาษาอังกฤษ การจะเป็นประโยคสมบูรณ์ได้นั้น ประโยคจะต้องประกอบไปด้วย 3 ส่วนสำคัญดังนี้ กริยา หรือ verb (ภาคขยาย) ภาคขยาย จะมีหรือไม่มีก็ได้ การใส่ภาคขยายเข้ามาเพื่อให้ประโยคสมบูรณ์ยิ่งขึ้น ประธาน subject + กริยา หรือ

การใช้ Tenses : Present Simple Tense/ Present Continuous Tense
สวัสดีนักเรียนชั้นม.2 ที่น่ารักทุกคน วันนี้เราจะไปดู “การใช้ Tenses : Present simple/ Present Continuous” พร้อมทั้งตัวอย่างสถานการณ์ใกล้ตัว หากพร้อมแล้วก็ไปลุยกันเลย ทบทวน Present Simple Tense ความหมาย: Present แปลว่า ปัจจุบัน ดังนั้น Present
บทความภาษาไทยแนะนำ

ถอดคำประพันธ์ กลอนดอกสร้อยรำพึงในป่าช้า พร้อมศึกษาคุณค่าในเรื่อง
ในบทเรียนก่อนหน้าเราได้เรียนรู้ประวัติความเป็นมา ลักษณะคำประพันธ์และเรื่องย่อกลอนดอกสร้อยรำพึงในป่าช้าไปแล้ว บทเรียนภาษาไทยในวันนี้จะต่อเนื่องกับครั้งก่อนโดยการพาน้อง ๆ ไปเรียนรู้เรื่องตัวบทเด่น ๆ ถอดคำประพันธ์ กลอนดอกสร้อยรำพึงในป่าช้า พร้อมทั้งศึกษาคุณค่าที่แฝงอยู่ในเรื่อง ไม่ว่าจะเป็นด้านสังคม เนื้อหา หรือด้านวรรณศิลป์ ถ้าน้อง ๆ พร้อมจะเรียนวรรณคดีเรื่องนี้ต่อไปแล้ว ก็ไปลุยพร้อมกันเลยค่ะ ถอดคำประพันธ์ กลอนดอกสร้อยรำพึงในป่าช้า สกุลเอ๋ยสกุลสูง ชักจูงจิตชูศักดิ์ศรี อำนาจนำความสง่าอ่าอินทรีย์

ศึกษาประวัติความเป็นมาและเรื่องย่อของเรื่องราชาธิราช ตอน สมิงพระรามอาสา
ราชาธิราช เป็นวรรณคดีประเภท พงศาวดาร ที่มีการแปลมาจากพงศาวดารมอญ น้อง ๆ หลายคนคงจะทราบกันดีอยู่แล้วว่าพงศาวดารก็คือเรื่องราวหรือเหตุการณ์ที่เกี่ยวกับประเทศชาติหรือพระมหากษัตริย์ แต่ทราบกันหรือไม่คะว่าทำไมในแบบเรียนภาษาไทยของเรานั้นถึงต้องเรียนเรื่องราชาธิราช ที่เป็นพงศาวดารมอญด้วย วันนี้เราจะพาน้อง ๆ ทุกคนไปเรียนรู้ประวัติความเป็นมาของเรื่องราชาธิราชรวมไปถึงเรื่องย่อ ซึ่งในบทที่เราจะเรียนนี้คือตอน สมิงพระรามอาสา เรื่องราวจะเป็นอย่างไรบ้าง ไปศึกษาเรื่องนี้พร้อม ๆ กันเลยค่ะ ราชาธิราช ประวัติความเป็นมา ราชาธิราชเป็นวรรณคดีร้อยแก้วที่พระบาทสมเด็จพระพุทธยอดฟ้าจุฬาโลกมหาราชโปรดเกล้าฯ

ความหมายและความสำคัญของ คำราชาศัพท์
คำราชาศัพท์ เป็นวัฒนธรรมทางภาษาของประเทศไทยที่ให้ความสำคัญกับระดับของผู้พูดและผู้ฟัง น้อง ๆ หลายคนคงคุ้นเคยกันมาบ้างแล้วเวลาฟังข่าวในพระราชสำนัก แต่รู้หรือไม่คะว่าความหมายจริง ๆ ของคำราชาศัพท์คืออะไร มีใครบ้างที่เราต้องใช้คำราชาศัพท์ด้วย บทเรียนภาษาไทยในวันนี้จะพาน้อง ๆ ไปทบทวนเรื่องคำราชาศัพท์พร้อมเรียนรู้คำราชาศัพท์ในหมวดร่างกายที่ใช้กับพระมหากษัตริย์กันค่ะ ความหมายของคำราชาศัพท์ คำราชาศัพท์ หมายถึง คำที่ใช้กับพระมหากษัตริย์ และพระบรมวงศานุวงศ์ รวมไปถึงพระสงฆ์ โดยที่มีคำศัพท์และลักษณะการใช้ที่แตกต่างกันออกไปตามระดับภาษา ฐานะของบุคคลในสังคมไทยแบ่งตามวัยวุฒิและชาติวุฒิได้ดังนี้ 1.

ดูคลิปบทเรียนสั้นๆ
แค่ 10 นาที ก็เข้าใจได้
สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ ภาษาไทย และชีววิทยา ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ
ล่าสุด
เรนจ์ของความสัมพันธ์
เรนจ์ของความสัมพันธ์ เรนจ์ของความสัมพันธ์ r คือ สมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหลัง เช่น = {(2, 2), (3, 5), (8, 10)} จะได้ว่า = {2, 5,
โดเมนของความสัมพันธ์
โดเมนของความสัมพันธ์ โดเมนของความสัมพันธ์ r คือ สมาชิกตัวหน้าของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหน้า เช่น = {(2, 2), (3, 4), (8, 9)} จะได้ว่า = {2, 3, 8}
กราฟของความสัมพันธ์
กราฟของความสัมพันธ์ กราฟของความสัมพันธ์ r คือเซตของจุดในระนาบx, y โดยที่แต่ละจุดคือสมาชิกของความสัมพันธ์ r นั่นเอง อธิบายให้เข้าใจง่ายคือ เมื่อเราได้เซตของความสัมพันธ์ r ที่มีสมาชิกในเซตคือคู่อันดับแล้ว เราก็นำคู่อันดับแต่ละคู่มาเขียนกราฟนั่นเอง เช่น r = {(1, 1), (1, 2), (2, 2), (3, 4)} นำมาเขียนกราฟของความสัมพันธ์

ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง
ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง เป็นการส่งสมาชิกจากของเซตหนึ่งเรียกเซตนั้นว่าโดเมน ส่งไปให้สมาชิกอีกเซตหนึ่งเซตนั้นเรียกว่าเรนจ์ จากบทความก่อนหน้าเราได้พูดถึงฟังก์ชันและการส่งสมาชิกในเซตไปแล้วบางส่วน ในบทความนี้เราจะได้ทำความเข้าใจเกี่ยวกับฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งมากขึ้น จากที่เรารู้ว่าเซตของคู่อันดับเซตหนึ่งจะเป็นฟังก์ชันได้นั้น สมาชิกตัวหน้าต้องไปเหมือนกัน แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งเป็นการกำหนดขอบเขตให้ฟังก์ชันนั้นแคปลงกว่าเดิม เช่น {(1, a), (2, b), (3, a), (4, c)} จากเซตของคู่อันดับเราสมารถตอบได้เลยว่าเป็นฟังก์ชัน เพราะสมาชิกตัวหน้าไม่เหมือนกัน แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง คือการที่เรามีเซต 2 เซต แล้วเราส่งสมาชิกในเซตหนึ่งไปอีกเซตหนึ่ง

การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์
การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ คือการตรวจสอบคู่อันดับว่าคู่ไหนเป็นความสัมพันธ์ที่ตรงกับเงื่อนไขที่กำหนด จากที่เรารู้กันในบทความเรื่อง ความสัมพันธ์ว่า r จะเป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A × B แต่ถ้าเราใส่เงื่อนไขบางอย่างเข้าไป ความสัมพันธ์ r ที่ได้ก็อาจจะจะเปลี่ยนไปด้วย แต่ยังคงเป็นสับเซตของ A × B เหมือนเดิม

Wh- Questions with do, does, did
สวัสดีน้องๆ ม. 3 ทุกคนนะครับ วันนี้เราจะมาเรียนรู้การถามคำถามโดยใช้ Wh- Questions ในภาษาอังกฤษกันครับ ถ้าพร้อมแล้วไปดูกันเลย

Phrasal Verbs: กริยาวลีในภาษาอังกฤษ
สวัสดีน้องๆ ม. 4 ทุกคนนะครับ วันนี้เราจะมาเรียนรู้เกี่ยวกับ two-word verbs และ three-word verb ในภาษาอังกฤษกันครับ จะเป็นอย่างไรเราไปดูกันเลย

Past Perfect Continuous Tense แบบเข้าใจแจ่มแจ้ง
สวัสดีน้องๆ ม. 6 ทุกคนนะครับ วันนี้เราจะมาทำทบทวนเกี่ยวกับ Past Perfect Continuous กันครับ ถ้าพร้อมแล้วเราไปเริ่มกันเลย

ความสัมพันธ์
ความสัมพันธ์ ความสัมพันธ์ เกิดจากสิ่งสองสิ่งมาเกี่ยวข้องกันภายใต้กฎเกณฑ์บางอย่าง เช่น ความสัมพันธ์ของ a กับ b ซึ่ง a มากกว่า b เป็นต้น ก่อนที่เราจะเริ่มเนื้อหาของความสำคัญพี่อยากให้น้องๆรู้จักกับคู่อันดับ และผลคูณคาร์ทีเซียนก่อนนะคะ คู่อันดับ ในการเขียนคู่อันดับเป็นสิ่งที่ค่อนข้างสำคัญเลยทีเดียว เพราะถ้าน้องๆเขียนคู่อันดับผิดตำแหน่งนั่นหมายความว่า ความหมายของมันจะเปลี่ยนไปทันที เช่น คู่อันดับ (x, y) โดย x

ฟังก์ชันและกราฟของฟังก์ชัน
ฟังก์ชันและกราฟของฟังก์ชัน ฟังก์ชันและกราฟของฟังก์ชัน มีความเกี่ยวข้องกันเนื่องจากฟังก์ชันที่เราเขียนในรูป y = f(x) สามารถนำไปเขียนกราฟในระบบพิกัดฉากได้ ซึ่งกราฟในระบบพิกัดฉากก็คือ กราฟที่ประกอบไปด้วยแกน x และ แกน y ก่อนที่เราจะเริ่มบทเรียนของฟังก์ชัน อยากให้น้องๆได้ศึกษารูปต่อไปนี้ก่อนนะคะ จากรูป คือการส่งสมาชิกในเซต A ไปยังสมาชิกในเซต B เซต A จะถูกเรียกว่า โดเมน

โจทย์ปัญหาการหารทศนิยม
บทความนี้เป็นเรื่องการวิเคราห์โจทย์ปัญหาการหารทศนิยม ซึ่งโจทย์ที่นำมาเป็นตัวอย่างจะประกอบด้วยการวิเคราะห์โจทย์ปัญหา การเขียนประโยคสัญลักษณ์ รวมไปถึงการสดงวิธีทำ หวังว่าน้องๆจะสามารถนำข้อมูลเหล่านี้ไปใช้ได้จริงกับโจทย์ปัญหาในห้องเรียน
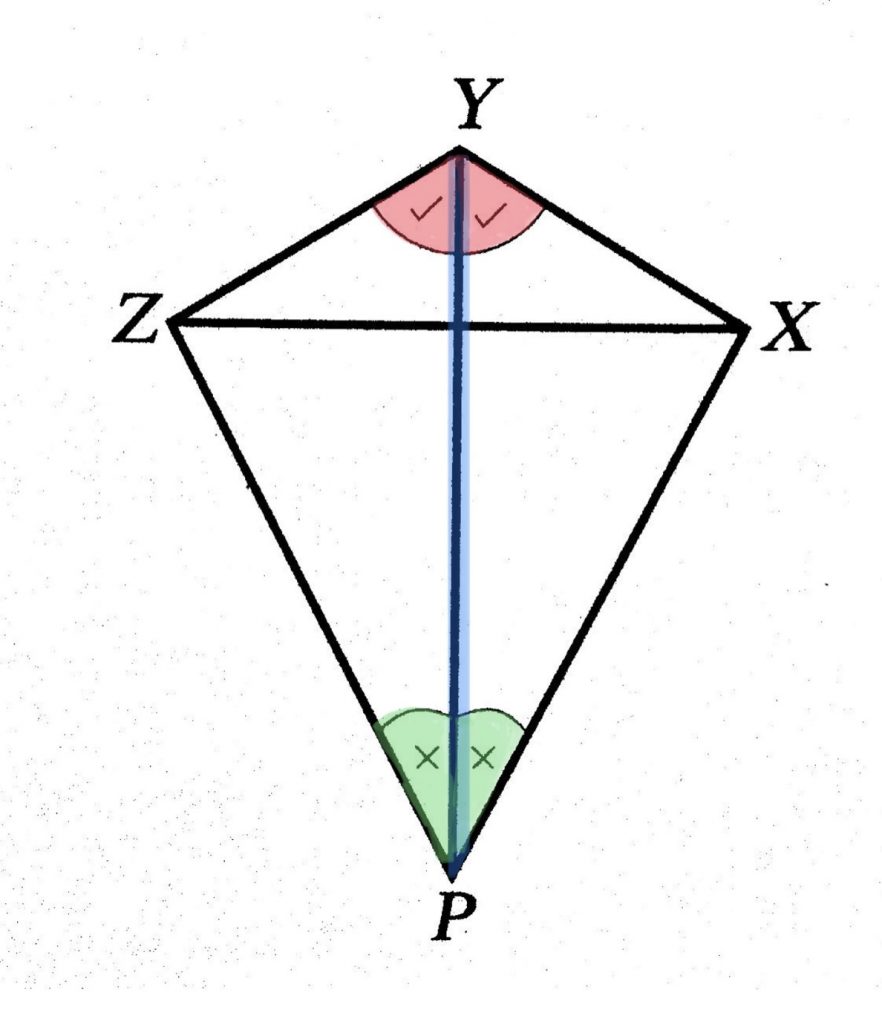
สามเหลี่ยมที่เท่ากันทุกประการแบบ มุม-ด้าน-มุม
ในบทความนี้จะกล่าวถึงหลักการของการพิสูจน์ความเท่ากันทุกประการของสามเหลี่ยมแบบ มุม-ด้าน-มุม
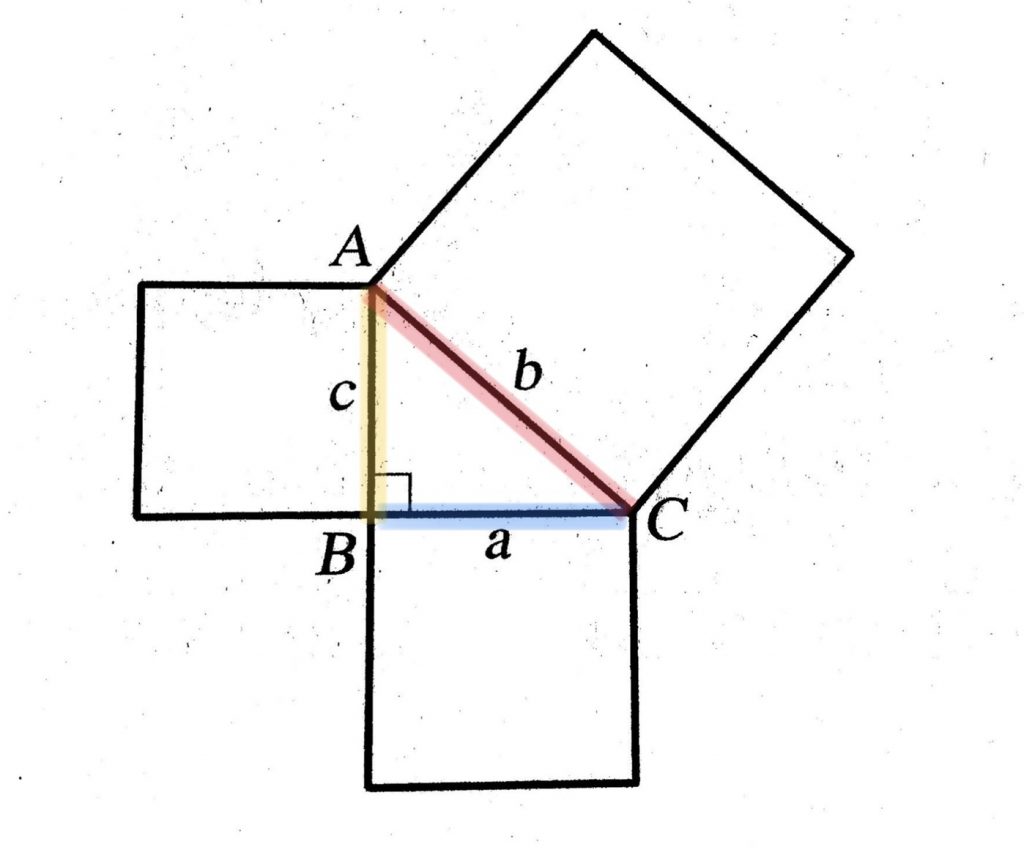
สมบัติของรูปสามเหลี่ยมมุมฉาก
ในบทความนี้นักเรียนจะได้เรียนรู้สมบัติของรูปสามเหลี่ยมมุมฉากที่ทำให้เข้าใจง่ายและมีวิธีในการวิเคราะห์โจทย์ที่หลากหลาย
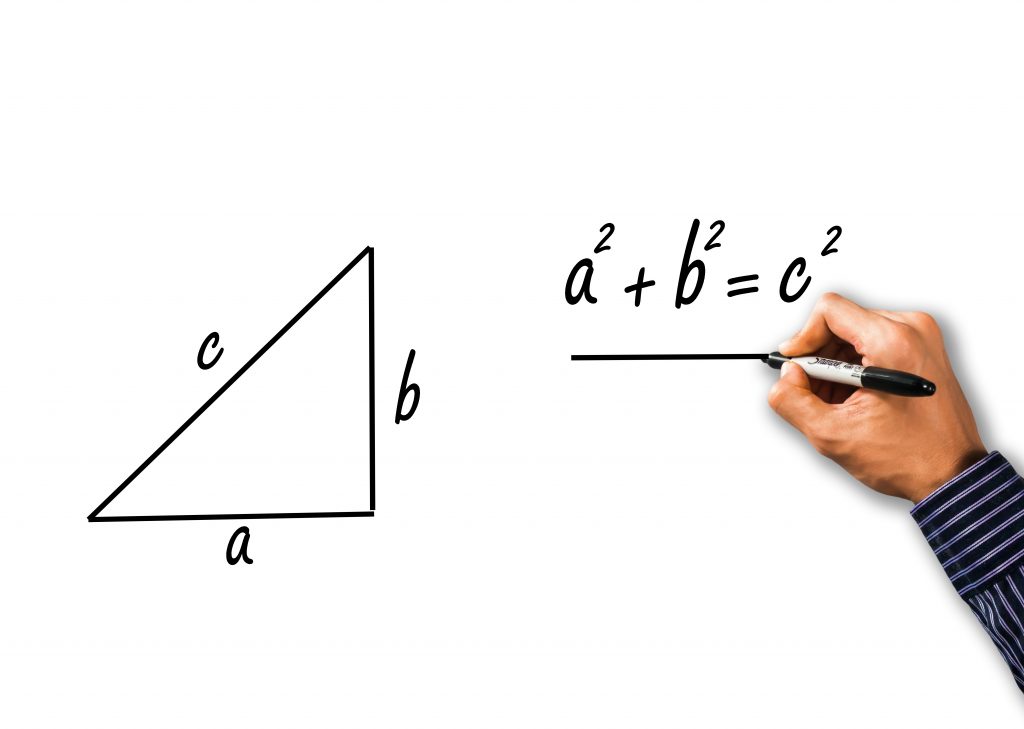
บทกลับของทฤษฎีบทพีทาโกรัส
ในบทความนี้เราจะได้เรียนรู้ความหมายและหลักการในการแสดงเหตุและผลของบทกลับของทฤษฎีบทพีทาโกรัส
สามเหลี่ยมที่เท่ากันทุกประการแบบ ด้าน-ด้าน-ด้าน
ในบทความนี้จะกล่าวถึงหลักการของการพิสูจน์ความเท่ากันทุกประการของสามเหลี่ยมแบบ ด้าน-ด้าน-ด้าน

เรนจ์ของความสัมพันธ์
เรนจ์ของความสัมพันธ์ เรนจ์ของความสัมพันธ์ r คือ สมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหลัง เช่น = {(2, 2), (3, 5), (8, 10)} จะได้ว่า = {2, 5,

โดเมนของความสัมพันธ์
โดเมนของความสัมพันธ์ โดเมนของความสัมพันธ์ r คือ สมาชิกตัวหน้าของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหน้า เช่น = {(2, 2), (3, 4), (8, 9)} จะได้ว่า = {2, 3, 8}
กราฟของความสัมพันธ์
กราฟของความสัมพันธ์ กราฟของความสัมพันธ์ r คือเซตของจุดในระนาบx, y โดยที่แต่ละจุดคือสมาชิกของความสัมพันธ์ r นั่นเอง อธิบายให้เข้าใจง่ายคือ เมื่อเราได้เซตของความสัมพันธ์ r ที่มีสมาชิกในเซตคือคู่อันดับแล้ว เราก็นำคู่อันดับแต่ละคู่มาเขียนกราฟนั่นเอง เช่น r = {(1, 1), (1, 2), (2, 2), (3, 4)} นำมาเขียนกราฟของความสัมพันธ์

ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง
ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง เป็นการส่งสมาชิกจากของเซตหนึ่งเรียกเซตนั้นว่าโดเมน ส่งไปให้สมาชิกอีกเซตหนึ่งเซตนั้นเรียกว่าเรนจ์ จากบทความก่อนหน้าเราได้พูดถึงฟังก์ชันและการส่งสมาชิกในเซตไปแล้วบางส่วน ในบทความนี้เราจะได้ทำความเข้าใจเกี่ยวกับฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งมากขึ้น จากที่เรารู้ว่าเซตของคู่อันดับเซตหนึ่งจะเป็นฟังก์ชันได้นั้น สมาชิกตัวหน้าต้องไปเหมือนกัน แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่งเป็นการกำหนดขอบเขตให้ฟังก์ชันนั้นแคปลงกว่าเดิม เช่น {(1, a), (2, b), (3, a), (4, c)} จากเซตของคู่อันดับเราสมารถตอบได้เลยว่าเป็นฟังก์ชัน เพราะสมาชิกตัวหน้าไม่เหมือนกัน แต่ฟังก์ชันจากเซตหนึ่งไปอีกเซตหนึ่ง คือการที่เรามีเซต 2 เซต แล้วเราส่งสมาชิกในเซตหนึ่งไปอีกเซตหนึ่ง

การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์
การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ คือการตรวจสอบคู่อันดับว่าคู่ไหนเป็นความสัมพันธ์ที่ตรงกับเงื่อนไขที่กำหนด จากที่เรารู้กันในบทความเรื่อง ความสัมพันธ์ว่า r จะเป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A × B แต่ถ้าเราใส่เงื่อนไขบางอย่างเข้าไป ความสัมพันธ์ r ที่ได้ก็อาจจะจะเปลี่ยนไปด้วย แต่ยังคงเป็นสับเซตของ A × B เหมือนเดิม

Wh- Questions with do, does, did
สวัสดีน้องๆ ม. 3 ทุกคนนะครับ วันนี้เราจะมาเรียนรู้การถามคำถามโดยใช้ Wh- Questions ในภาษาอังกฤษกันครับ ถ้าพร้อมแล้วไปดูกันเลย

Phrasal Verbs: กริยาวลีในภาษาอังกฤษ
สวัสดีน้องๆ ม. 4 ทุกคนนะครับ วันนี้เราจะมาเรียนรู้เกี่ยวกับ two-word verbs และ three-word verb ในภาษาอังกฤษกันครับ จะเป็นอย่างไรเราไปดูกันเลย

Past Perfect Continuous Tense แบบเข้าใจแจ่มแจ้ง
สวัสดีน้องๆ ม. 6 ทุกคนนะครับ วันนี้เราจะมาทำทบทวนเกี่ยวกับ Past Perfect Continuous กันครับ ถ้าพร้อมแล้วเราไปเริ่มกันเลย

ความสัมพันธ์
ความสัมพันธ์ ความสัมพันธ์ เกิดจากสิ่งสองสิ่งมาเกี่ยวข้องกันภายใต้กฎเกณฑ์บางอย่าง เช่น ความสัมพันธ์ของ a กับ b ซึ่ง a มากกว่า b เป็นต้น ก่อนที่เราจะเริ่มเนื้อหาของความสำคัญพี่อยากให้น้องๆรู้จักกับคู่อันดับ และผลคูณคาร์ทีเซียนก่อนนะคะ คู่อันดับ ในการเขียนคู่อันดับเป็นสิ่งที่ค่อนข้างสำคัญเลยทีเดียว เพราะถ้าน้องๆเขียนคู่อันดับผิดตำแหน่งนั่นหมายความว่า ความหมายของมันจะเปลี่ยนไปทันที เช่น คู่อันดับ (x, y) โดย x

ฟังก์ชันและกราฟของฟังก์ชัน
ฟังก์ชันและกราฟของฟังก์ชัน ฟังก์ชันและกราฟของฟังก์ชัน มีความเกี่ยวข้องกันเนื่องจากฟังก์ชันที่เราเขียนในรูป y = f(x) สามารถนำไปเขียนกราฟในระบบพิกัดฉากได้ ซึ่งกราฟในระบบพิกัดฉากก็คือ กราฟที่ประกอบไปด้วยแกน x และ แกน y ก่อนที่เราจะเริ่มบทเรียนของฟังก์ชัน อยากให้น้องๆได้ศึกษารูปต่อไปนี้ก่อนนะคะ จากรูป คือการส่งสมาชิกในเซต A ไปยังสมาชิกในเซต B เซต A จะถูกเรียกว่า โดเมน

โจทย์ปัญหาการหารทศนิยม
บทความนี้เป็นเรื่องการวิเคราห์โจทย์ปัญหาการหารทศนิยม ซึ่งโจทย์ที่นำมาเป็นตัวอย่างจะประกอบด้วยการวิเคราะห์โจทย์ปัญหา การเขียนประโยคสัญลักษณ์ รวมไปถึงการสดงวิธีทำ หวังว่าน้องๆจะสามารถนำข้อมูลเหล่านี้ไปใช้ได้จริงกับโจทย์ปัญหาในห้องเรียน

สามเหลี่ยมที่เท่ากันทุกประการแบบ มุม-ด้าน-มุม
ในบทความนี้จะกล่าวถึงหลักการของการพิสูจน์ความเท่ากันทุกประการของสามเหลี่ยมแบบ มุม-ด้าน-มุม

สมบัติของรูปสามเหลี่ยมมุมฉาก
ในบทความนี้นักเรียนจะได้เรียนรู้สมบัติของรูปสามเหลี่ยมมุมฉากที่ทำให้เข้าใจง่ายและมีวิธีในการวิเคราะห์โจทย์ที่หลากหลาย
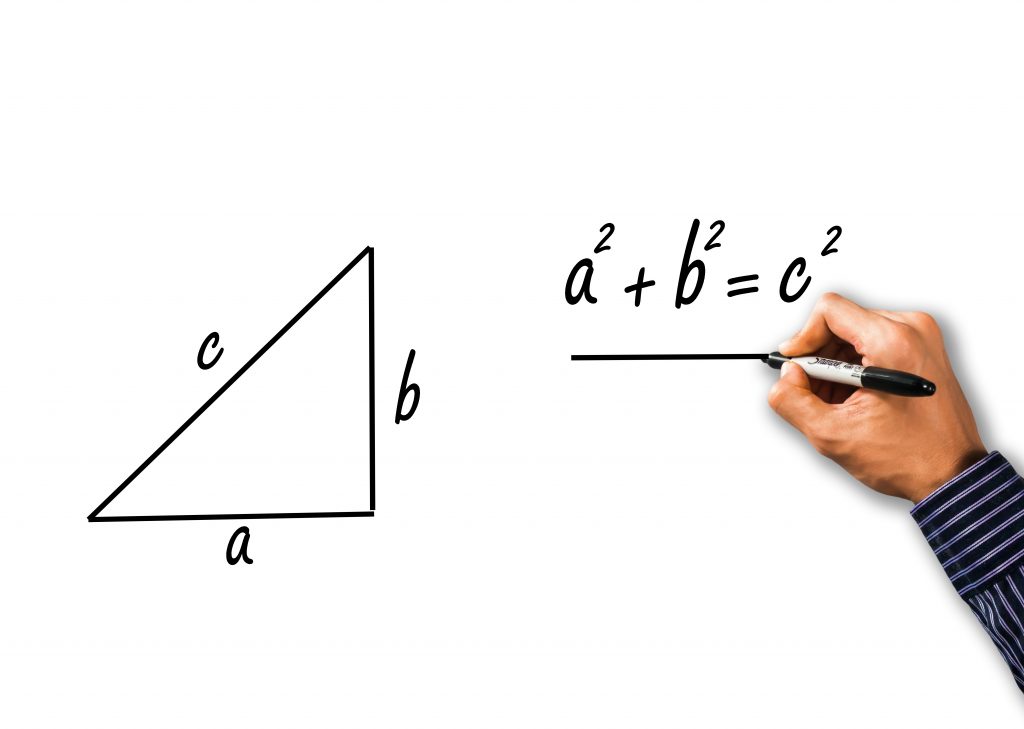
บทกลับของทฤษฎีบทพีทาโกรัส
ในบทความนี้เราจะได้เรียนรู้ความหมายและหลักการในการแสดงเหตุและผลของบทกลับของทฤษฎีบทพีทาโกรัส

สามเหลี่ยมที่เท่ากันทุกประการแบบ ด้าน-ด้าน-ด้าน
ในบทความนี้จะกล่าวถึงหลักการของการพิสูจน์ความเท่ากันทุกประการของสามเหลี่ยมแบบ ด้าน-ด้าน-ด้าน




