รวม 16 บทความ
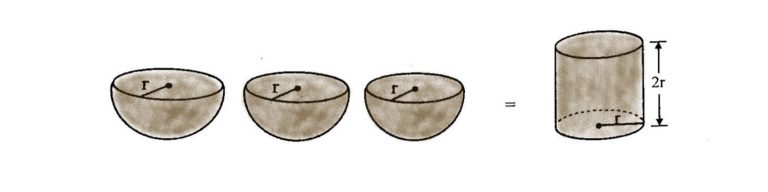
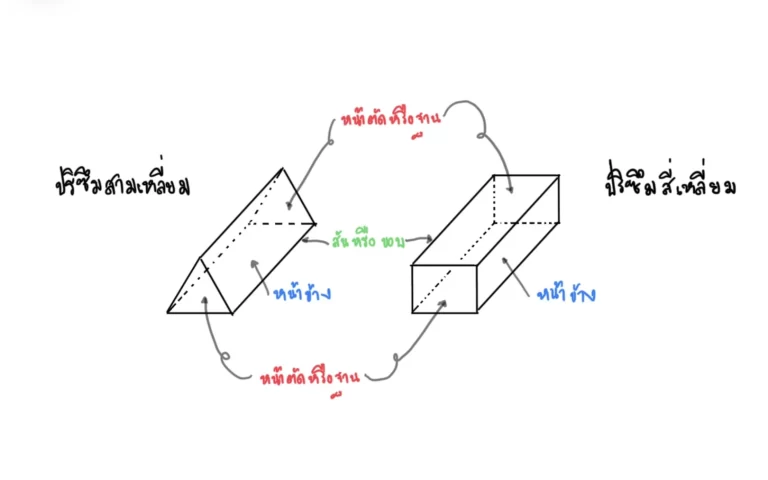
พื้นที่ผิวทรงกรวยและลูกบาศก์ การหาพื้นที่ผิวทรงกรวยเเละลูกบาศก์นั้นมักเป็นสิ่งที่เราอาจได้ใช้ในชีวิตประจำวัน ทั้งเรื่องการออกเเบบทางวิศวกรรม หรือสถาปัตยกรรม ที่ต้องนำพื้นที่ผิวมาประเมินค่าใช้จ่ายในการทาสี, การปูกระเบื้อง, หรือเเม้กระทั่งปริ…
การแก้โจทย์ปัญหาโดยใช้ระบบสมการเชิงเส้นสองตัวแปร บทความนี้ได้รวบรวมความรู้เรื่อง การแก้โจทย์ปัญหาโดยใช้ระบบสมการเชิงเส้นสองตัวแปร น้องๆจะต้องวิเคราะห์โจทย์ปัญหา แปลงโจทย์ปัญหาให้เป็นสมการ 2 สมการขึ้นไป และแก้สมการเพื่อหาคำตอบ ซึ่งก่อนที่จะเ…
การแก้ระบบสมการเชิงเส้นสองตัวแปร บทความนี้ได้รวบรวมความรู้เรื่อง การแก้ระบบสมการเชิงเส้นสองตัวแปร โดยการเลือกกำจัดตัวแปรใดตัวแปรหนึ่ง(x) เมื่อเลือกกำจัด x จะได้ค่า y แล้วนำค่าของตัวแปร(y) มาแทนค่าในสมการเพื่อหาค่าของตัวแปรอีกหนึ่งตัวแปร (x)…
การแก้ระบบสมการเชิงเส้นสองตัวแปร โดยใช้กราฟ บทความนี้ได้รวบรวมความรู้เรื่อง การแก้ระบบสมการเชิงเส้นสองตัวแปร โดยใช้กราฟ ทำได้โดยนำตัวเลขแทนค่าตัวแปร แล้วจะได้กราฟของสมการเชิงเส้นสองตัวแปรเป็นกราฟเส้นตรง สังเกตกราฟที่ได้ว่าตัดกัน ขนานกัน หรื…
ความน่าจะเป็นกับการตัดสินใจ บทความนี้ได้รวบรวมความรู้เรื่อง ความน่าจะเป็นกับการตัดสินใจ สำหรับบางเหตุการณ์ความรู้เรื่องความน่าจะเป็นเพียงอย่างเดียว อาจไม่เพียงพอที่จะช่วยตัดสินใจได้ จำเป็นจะต้องหาองค์ประกอบอื่นมาช่วยในการตัดสินใจด้วย นั่นคื…
ความน่าจะเป็นของเหตุการณ์ บทความนี้ได้รวบรวมความรู้เรื่อง ความน่าจะเป็นของเหตุการณ์ ซึ่งได้กล่าวถึงขั้นตอนและวิธีการหาความน่าจะเป็นของเหตุการณ์ และยกตัวอย่างประกอบ อธิบายอย่างละเอียด ซึ่งก่อนจะเรียนเรื่อง ความน่าจะเป็นของเหตุการณ์น้องๆสามาร…
บทความนี้ได้รวบรวมความรู้เรื่อง การทดลองสุ่มและเหตุการณ์ ซึ่งได้กล่าวถึงในลักษณะของความหมายและยกตัวอย่างประกอบ และอธิบายอย่างละเอียด ซึ่งก่อนจะเรียนเรื่อง การทดลองสุ่มและเหตุการณ์ น้องๆสามารถทบทวน ความน่าจะเป็น ได้ที่ ⇒⇒ ความน่าจะเป็น ⇐⇐ กา…
บทความนี้ได้รวบรวมความรู้เรื่อง สถิติ (เส้นโค้งความถี่) ซึ่งก่อนที่จะเรียนเรื่องนี้ น้องๆจะต้องมีความรู้ในเรื่อง ค่ากลางของข้อมูล และการวัดการกระจายของข้อมูล สามารถศึกษาเพิ่มเติมได้ที่ ⇒⇒ สถิติ (ค่ากลางของข้อมูล/การกระจายของข้อมูล) ⇐⇐ เส้นโ…
บทความนี้จะแนะนำให้รู้จักกับ ความน่าจะเป็น ซึ่งได้กล่าวถึงในลักษณะของความหมายและยกตัวอย่างประกอบ รวมถึงคำที่เกี่ยวข้องกับความน่าจะเป็น เช่นการทดลองสุ่ม ปริภูมิตัวอย่าง และเหตุการณ์ ดังต่อไปนี้ ความน่าจะเป็น ความน่าจะเป็น (Probability) เป็นจ…
บทความนี้ได้รวบรวมความรู้เรื่อง ค่ากลางของข้อมูลและการกระจายของข้อมูล ซึ่งค่ากลางของข้อมูลจะประกอบด้วย ค่าเฉลี่ยเลขคณิต มัธยฐาน และฐานนิยม ส่วนการวัดการกระจายของข้อมูลจะศึกษาในเรื่องการหาส่วนเบี่ยงเบนมาตรฐาน ซึ่งน้องๆสามารถทบทวน การนำเสนอข้…
บทความนี้ได้รวบรวม โจทย์ปัญหาเกี่ยวกับอสมการเชิงเส้นตัวแปรเดียว ไว้หลากหลายตัวอย่าง ซึ่งแสดงวิธีคิดอย่างละเอียด สามารถเรียนรู้และเข้าใจได้ง่าย แต่ก่อนที่น้องๆจะได้เรียนรู้การแก้อโจทย์ปัญหาเกี่ยวกับอสมการเชิงเส้นตัวแปรเดียว น้องๆสามารถทบทวน…
บทความนี้จะเป็นการสอนวิธี การแก้อสมการเชิงเส้นตัวแปรเดียว ซึ่งสามารถทำได้โดยการจัดรูปของตัวแปรให้อยู่ด้านเดียวกันและตัวเลขอยู่อีกด้าน เพื่อหาค่าของตัวแปรนั้นๆ แต่ก่อนที่น้องๆจะได้เรียนรู้การแก้อสมการนั้น น้องๆสามารถทบทวน อสมการเชิงเส้นตัวแป…
ยังมีฟีเจอร์อีกมากมายในแอปของเรา
ไปหน้าคลิป