ในทางคณิตศาสตร์ เราอาจคำนวณหาปริมาตรของสิ่งของต่างๆได้โดยไม่ต้องใช้การแทนที่น้ำ ในบทเรียนนี้นักเรียนจะได้เรียนการหาปริมาตรของรูปเรขาคณิตสามมิติหลายชนิด ซึ่งในกรณีที่รูปเรขาคณิตนั้นมีฐานทั้งสองข้างเป็นรูปเหลี่ยมที่เท่ากันทุกประการหรือเป็นวงกลมที่เท่ากันทุกประการและอยู่ในระนาบที่ขนานกัน นั่นมายถึง ปริมาตรของปริซึมและทรงกระบอก
ปริซึมและทรงกระบอกในชีวิตประจำวัน
- บุคคลในหลายสาขาอาชีพต้องเข้าใจและชำนาญในเรื่องของการวัด การชั่ง การตวง และเรื่องที่เกี่ยวกับปริมาตรเป็นอย่างดี ไม่เช่นนั้นอาจทำให้เกิดข้อผิดพลาดและเสียหาย เช่น วิศวกรอาจออกแบบโครงสร้างของสิ่งก่อสร้างต่าง ๆ ได้ไม่แข็งแรงพอ นักวิทยาศาสตร์อาจทำการทดลองแล้วผิดพลาดทำให้เกิดการระเบิด หรือพ่อครัวอาจปรุงอาหารแล้วได้รสชาติไม่คงที่
- สำหรับบุคคลทั่วไป การเรียนรู้และใช้ความรู้เกี่ยวกับปริมาตรจะช่วยให้เราเป็นผู้บริโภคที่ฉลาดในการเลือกซื้อสินค้า รู้จักเปรียบเทียบราคาของสินค้าต่อหน่วยปริมาตร ทำให้เลือกซื้อสินค้าได้ถูกกว่าและช่วยให้เราประหยัดค่าใช้จ่ายได้
- เมื่อกล่าวถึงการวัดความจุ จะหมายถึงการหาปริมาตรการหาปริมาตรของวัตถุใด ๆ อาจทำได้โดยการจมวัตถุนั้นลงในภาชนะที่มีน้ำอยู่ ตราบใดที่วัตถุไม่ละลายหรือดูดซับน้ำ ปริมาตรของน้ำส่วนที่เพิ่มขึ้น หรือปริมาตรของน้ำที่ล้นออกมาในกรณีที่เดิมมีน้ำอยู่เต็มภาชนะพอดี จะเท่ากับปริมาตรของวัตถุนั้น วิธีการนี้เป็นการหาปริมาตรของวัตถุโดยการแทนที่น้ำ
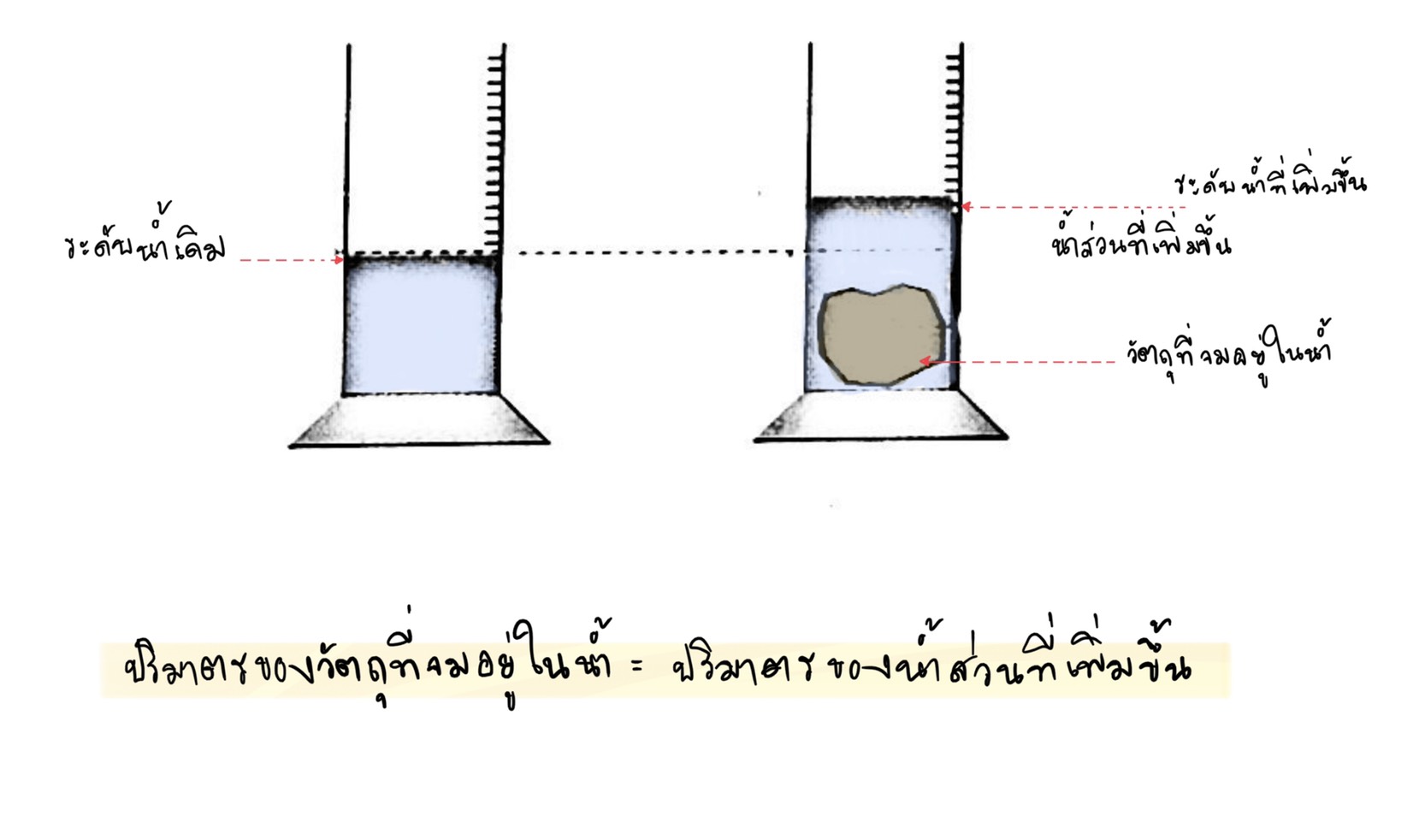
ปริมาตรของปริซึม
ทรงสี่เหลี่ยมมุมฉากเป็นปริซึมชนิดหนึ่งที่เรียกว่า ปริซึมสี่เหลี่ยมมุมฉาก นักเรียนรู้จักการหาปริมาตรของทรงสี่เหลี่ยมมุมฉากมาแล้ว ดังนั้น สูตรการหาปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก จึงเป็นสูตรเดียวกันกับสูตรการหาปริมาตรของทรงสี่เหลี่ยมมุมฉาก กล่าวคือ
ปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก = ความกว้าง x ความยาว x ความสูง
=พื้นที่ฐาน x ความสูง
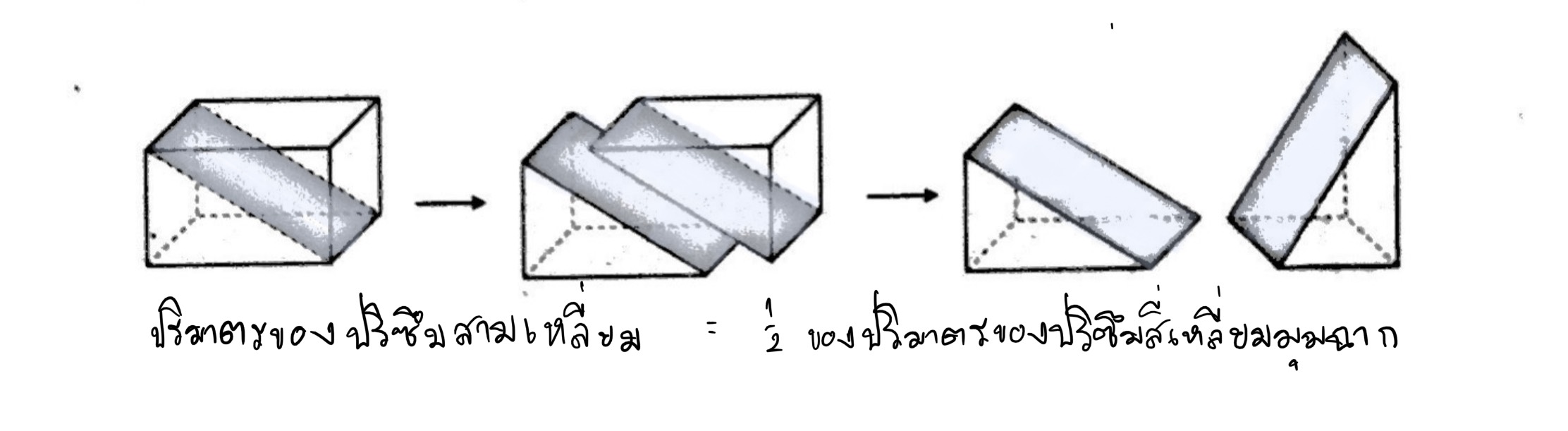
สำหรับปริมาตรของปริซึมสามเหลี่ยมใด ๆ หาได้โดยอาศัยวิธีหาปริมาตรของปริซึมสามเหลี่ยมมุมฉากดังนี้
ให้นักเรียนพิจารณาการตัดปริซึมสี่เหลี่ยมมุมฉากตามระนาบที่แรเงาดังแสดงในรูป จะได้รูปเรขาคณิตสามมิติสองรูปที่มีขนาดและรูปร่างเป็นอย่างเดียวกัน รูปเรขาคณิตสามมิติทั้งสองรูปเป็นปริซึมสามเหลี่ยมมุมฉากที่มีปริมาตรเท่ากัน แต่ละรูปมีปริมาตรเป็นครึ่งหนึ่งของปริมาตรของปริซึมสี่เหลี่ยมมุมฉาก
เราสามารถนำสูตรการหาปริมาตรของปริซึมสามเหลี่ยมใด ๆ ไปหาสูตรของปริซึมที่มีฐานเป็นรูปหลายเหลี่ยมได้โดยแบ่งฐานของปริซึมหลายเหลี่ยมนั้นออกเป็นรูปสามเหลี่ยมหลาย ๆ รูปตัวอย่างเช่นเราแบ่งปริซึมห้าเหลี่ยมซึ่งสูง h หน่วยออกเป็นปริซึมสามเหลี่ยม 3 รูปได้ ดังนี้

ปริมาตรของทรงกระบอก
นักเรียนลองนึกภาพของรูปหลายเหลี่ยมด้านเท่ามุมเท่าตามลำดับที่กำหนดให้ข้างล่างนี้ เริ่มจากรูปสามเหลี่ยมด้านเท่า รูปสี่เหลี่ยมจัตุรัส รูปห้าเหลี่ยมด้านเท่ามุมเท่า รูปหกเหลี่ยมด้านเท่ามุมเท่า รูปเจ็ดเหลี่ยมด้านเท่ามุมเท่า และรูปแปดเหลี่ยมด้านเท่ามุมเท่า จะสังเกตเห็นว่ายิ่งจำนวนด้านมีมากขึ้นเท่าใด รูปหลายเหลี่ยมด้านเท่ามุมเท่าเหล่านั้นก็จะมีรูปร่างใกล้เคียงกับวงกลมมากขึ้นตามไปด้วย

เราอาจกล่าวได้ว่า ทรงกระบอกจึงมีลักษณะใกล้เคียงกับปริซึมที่มีฐานเป็นรูปหลายเหลี่ยมด้านเท่ามุมเท่าที่มีจำนวนด้านมาก ๆ ดังนั้นการหาปริมาตรของทรงกระบอกจึงหาได้ในทำนองเดียวกันกับการหาปริมาตรของปริซึมนั่นเอง