โดเมนของความสัมพันธ์

โดเมนของความสัมพันธ์ r คือ สมาชิกตัวหน้าของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย

กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหน้า

เช่น = {(2, 2), (3, 4), (8, 9)}

จะได้ว่า  = {2, 3, 8}

กรณีที่ r เขียนในรูปแบบที่บอกเงื่อนไข เราอาจจะสามารถนำมาเขียนแบบแจกแจงสมาชิกได้

เช่น ให้ A = {1, 2, 3} และ = {(x, y) ∈ A × A : y = 2x}

x = 1 ; y = 2(1) = 2

x = 2 ; y = 2(2) = 4

x = 3 ; y = 2(3) = 6

ได้คู่อันดับ ดังนี้ (1, 2), (2, 4), (3, 6) เนื่องจาก (x, y) ต้องเป็นสมาชิกใน A × A

และจาก (1, 2) ∈ A × A

(2, 4) ∉ A × A

(3, 6) ∉ A × A

ดังนั้น สามารถเขียน r ในรูปแจกแจงสมาชิกได้ดังนี้  = {(1, 2)}

สรุปได้ว่า = {1}

แต่บางกรณีเราไม่สามารถแจกแจงสมาชิกได้ เช่น ให้ x, y เป็นจำนวนจริงใดๆ และ = {(x, y) : y = }

โดเมนของ คือ ค่า x ทุกตัวที่เป็นไปได้ ที่ทำให้ y เป็นจำนวนจริง

การที่จะหา x ที่ทำให้ y เป็นจำนวนจริงนั้น จำนวนของ x ที่เป็นไปได้มีเยอะมากๆๆๆๆ หายังไงก็ไม่หมดแน่นอน เราจึงต้องเปลี่ยนมา x ที่ทำให้ y ไม่เป็นจำนวนจริง ถ้าไม่มี เราสามารถตอบได้เลยว่า โดเมนคือ จำนวนจริง

แต่! ในตัวอย่างนี้เหมือนจะมี x ที่ทำให้ y ไม่เป็นจำนวนจริง นั่นคือ x = 0 จะได้ว่า y = ซึ่ง ไม่นิยาม

ดังนั้น โดเมนคือ จำนวนจริงทั้งหมดยกเว้น 0 เขียนได้เป็น = – {0}

ตัวอย่างการหาโดเมนของความสัมพันธ์

1.) ให้ A = {1, 2, 3} และ r = {(x, y) : y = 2x , x ∈ A}

จาก x เป็นสมาชิกใน A 

x = 1 ; y = 2(1) = 2

x = 2 ; y = 4

x = 3 ; y = 6

r = {(1, 2), (2, 4), (3, 6)}

ดังนั้น = {1, 2, 3} = A

2.) ให้ r = {(x, y) ∈ : y = x²}

เงื่อนไขของ (x, y) ∈  

พิจารณากราฟ y = x²

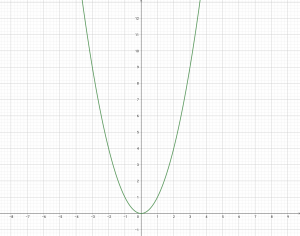
จะเห็นว่าค่ากราฟนั้นกางออกเรื่อยๆ  ค่า x เป็นไปได้เรื่อยๆไม่สิ้นสุด จาก โดเมนของความสัมพันธืคือ สมาชิกตัวหน้าของความสัมพันธ์ใน r นั่นคือ x นั่นเอง

ดังนั้น =

3.) ให้ r = {(x, y) : y = } และ x, y เป็นจำนวนจริงใดๆ

พิจารณากราฟของ y = จะได้

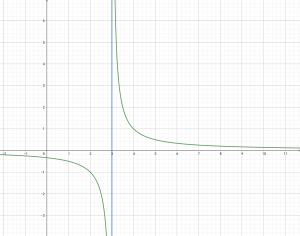
จะเห็นได้ว่า กราฟในรูปนั้น x เป็นอะไรก็ได้ ยกเว้น 3 เพราะ  เมื่อลองลากเส้น x = 3 แล้ว กราฟของ y = นั้นไม่ตัดกับเส้น x = 3 เลย

หรือเราลองสังเกตจากสมการก็ได้ว่า ถ้า x = 3 จำทำให้ตัวส่วนเป็น 0 ซึ่งหาค่าไม่ได้ (ไม่นิยาม) ดังนั้น x อยู่ใน R ยกเว้น 3

และโดเมนก็คือ ค่า x เพราะ x เป็นสมาชิกตัวหน้าของความสัมพันธ์ r 

ดังนั้น = R – {3} หรือ = {x : x ∈ R และ x ≠ 3}

4.) ให้ r = {(x, y) : y = } และ x, y เป็นจำนวนจริงใดๆ

พิจารณากราฟของสมการ y =

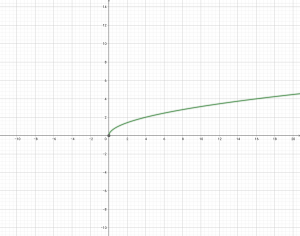
จะเห็นว่ากราฟที่ได้ x มีค่าตั้งแต่ 0 ไปเรื่อยๆ ไม่สิ้นสุด นั่นคือ x เป็นจำนวนจริงที่มากกว่าเท่ากับ 0

และโดเมนก็คือ ค่า x เพราะ x เป็นสมาชิกตัวหน้าของความสัมพันธ์ r 

ดังนั้น = {x : x เป็นจำนวนจริง และ x ≥ 0}

วิดีโอ โดเมนของความสัมพันธ์

เนื้อหาที่เกี่ยวข้องกับโดเมนของความสัมพันธ์

1. กราฟของความสัมพันธ์