วงรี

supanaree

คณิตศาสตร์, คณิตศาสตร์เพิ่มเติม, ภาคตัดกรววย, ม.4

Add LINE friends for one click to find article.

วงรี

วงรี จะประกอบไปด้วย

1) แกนเอกคือแกนที่ยาวที่สุด และแกนโทคือแกนที่สั้นกว่า

2) จุดยอด

3) จุดโฟกัส ซึ่งจะแตกต่างกันไปแล้วแต่ว่าแกนใดเป็นแกนเอก

4) ความเยื้องศูนย์กลาง (eccentricity)

วงรี ที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิด

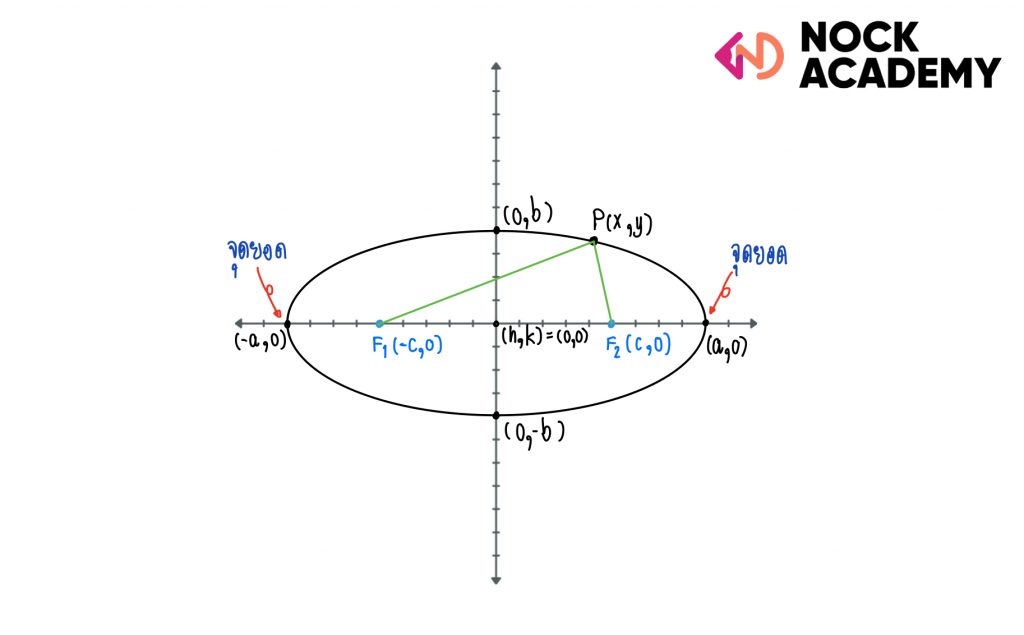
จากกราฟ
สมการรูปแบบมาตรฐาน: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
จุดยอด : (a, 0) และ (-a, 0)
แกนเอก : แกน X ยาว 2a
แกนโท : ยาว 2b
โฟกัส : (c, 0) และ (-c, 0)
ความเยื้องศูนย์กลาง(eccentricity): $e=\frac{c}{a}$

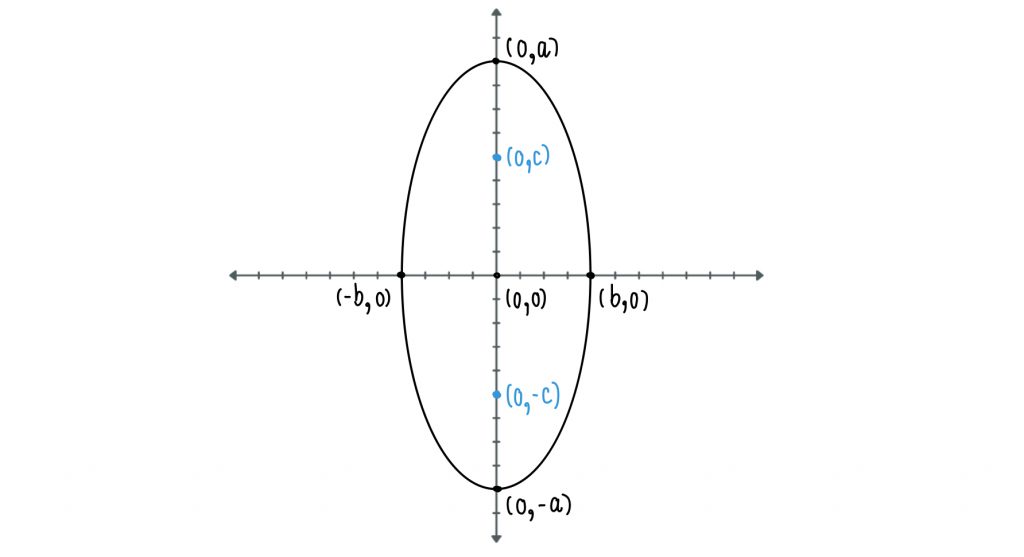
จากกราฟ
สมการรูปแบบมาตรฐาน: $\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$
จุดยอด : (0, a) (0, -a)
แกนเอก : แกน Y ยาว 2a
แกนโท : ยาว 2b
โฟกัส : (0, c) และ (0, -c)
ความเยื้องศูนย์กลาง(eccentricity): $e=\frac{c}{a}$

***ความเยื้องศูนย์กลางของวงรี คือ อัตราส่วนของ c ต่อ a เมื่อ $c=\sqrt{a^2-b^2}$ ***

วงรีที่มีจุดศูนย์กลางที่ (h, k)

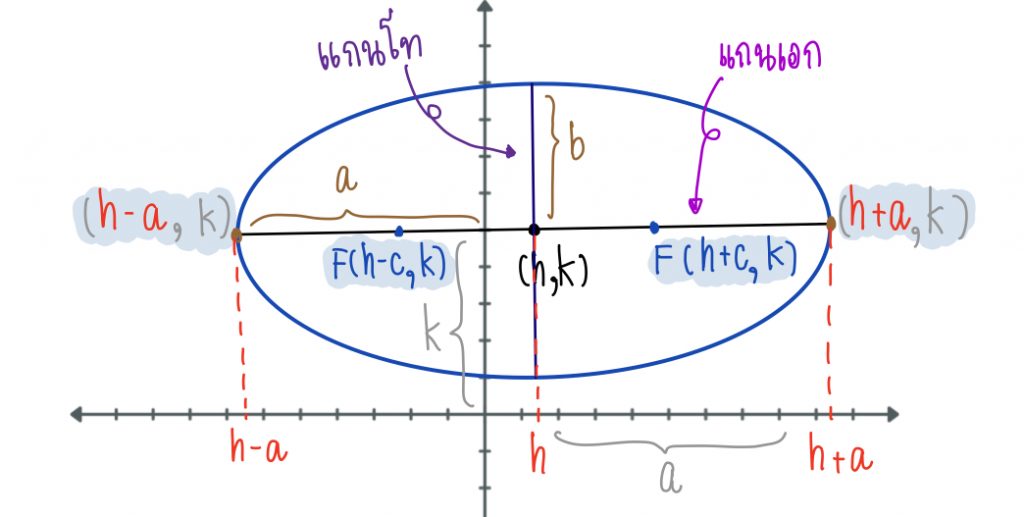
แกนเอกขนานแกน X

สมการรูปแบบมาตรฐาน: $\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$
จุดยอด : (h + a, k) และ (h – a, k)
แกนเอก : ยาว 2a
แกนโท : ยาว 2b
โฟกัส : (h + c, k) และ (h – c, k)

แกนเอกขนานแกน Y

สมการรูปแบบมาตรฐาน : $\frac{(y-k)^2}{a^2}+\frac{(x-h)^2}{b^2}=1$
จุดยอด : (h, k + a) (h, k – a)
แกนเอก : ยาว 2a
แกนโท : ยาว 2b
โฟกัส : (h, k + c) และ (h, k – c)

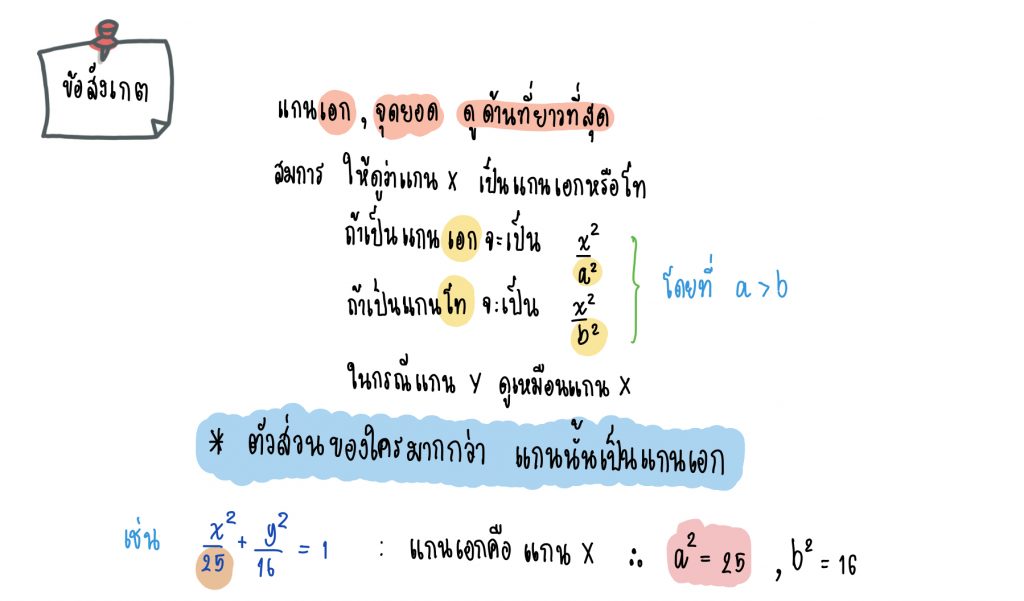
ตัวอย่าง

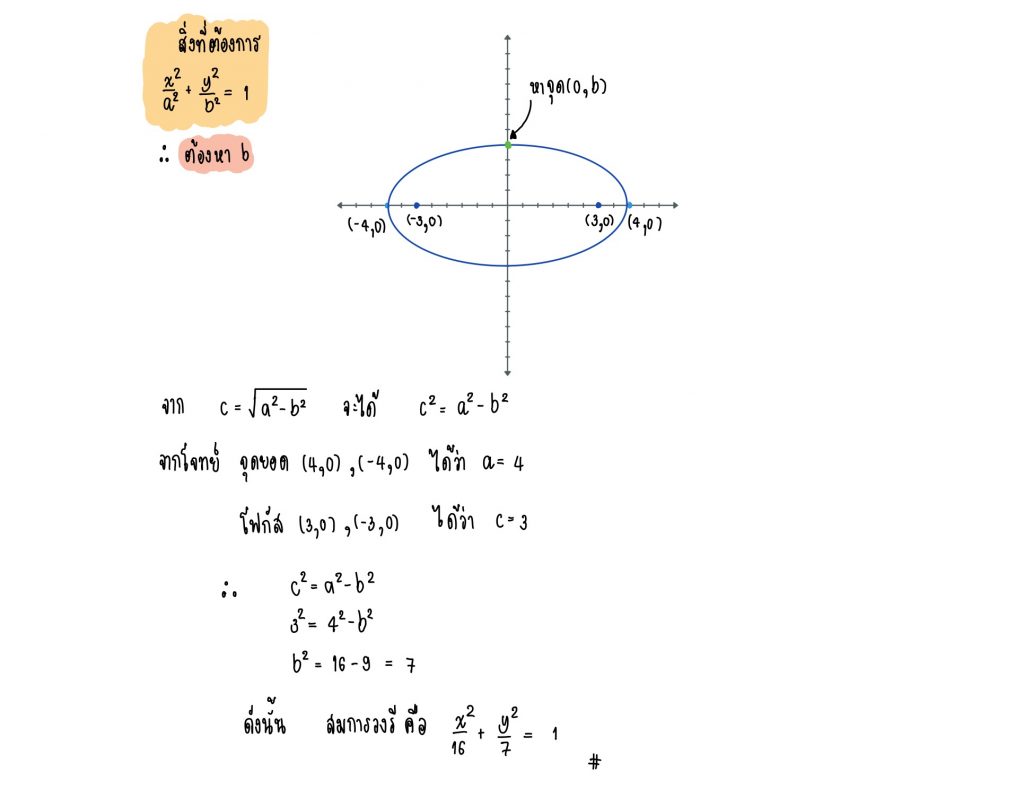
1. จงหาโฟกัสของวงรีที่มีสมการคือ

2. วงรีรูปหนึ่ง มีจุดยอดอยู่ที่ (4,0) และ (-4,0) และโฟกัสอยู่ที่ (3,0) และ (-3,0) จงหาสมการของวงรี

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

วิธีเขียน คำขวัญ ให้ถูกใจคนอ่าน

น้อง ๆ หลายคนคงจะคุ้นเคยกับคำขวัญกันเป็นอย่างนี้ เพราะในวันสำคัญต่าง ๆ อย่างวันเด็ก นายกรัฐมนตรีของประเทศในแต่ละสมัยก็จะให้คำขวัญแก่เด็ก ๆ ทุกปี แต่ทราบหรือไม่คะว่า คำขวัญ นั้นคืออะไรกันแน่ มีจุดมุ่งหมาย ลักษณะ และวิธีการเขียนอย่างไร บทเรียนในวันนี้จะพาน้อง ๆ ไปเรียนรู้เรื่องราวทั้งหมดนั้นของคำขวัญ ถ้าพร้อมแล้วเราไปเรียนรู้พร้อมกันเลยค่ะ คำขวัญ คืออะไร คำขวัญ คือ

การใช้ Yes/No Questions และ Wh-Questions

สวัสดีค่ะนักเรียนชั้นม.3 ทุกคน วันนี้ครูจะพาไปตะลุยตัวอย่างและวิธีการแต่งประโยคคำถาม 2กลุ่ม ได้แก่ “การใช้ Yes/No Questions และ Wh-Questions” หากพร้อมแล้วก็ไปลุยกันเลยจร้า Yes/No Questions คืออะไร? Yes/ No Questions ก็คือ กลุ่มคำถามที่ต้องการคำตอบแน่ชัดว่า Yes ใช่ หรือ

Short question เน้นรูปอดีตโดยใช้ Did, Was, Were

สวัสดีค่ะนักเรียนชั้นม.3 ที่น่ารักทุกคน วันนี้เราจะไปเรียนรู้เรื่อง “Short question เน้นรูปอดีตโดยใช้ Did, Was, Were” ไปลุยกันโลดเด้อ ทำไมต้องเรียนเรื่อง Did, Was, Were Did, Was, Were ใช้ถามคำถามใน Past Simple Tense กับเหตุการณ์ที่เกิดขึ้นและจบลงไปแล้วในอดีต หรือ ถามเพื่อให้แน่ใจว่าได้ทำสิ่งนั้นๆไปแล้ว

เห็นแก่ลูก ศึกษาความเป็นมาบทละครพูดเรื่องแรกของไทย

บทละครพูด เห็นแก่ลูก เป็นวรรณคดีเรื่องแรกที่น้อง ๆ ม.3 ทุกคนจะได้เรียน ความพิเศษของวรรณคดีไทยเรื่องนี้คือเป็นบทละครพูดเรื่องแรกของไทยอีกทั้งยังได้รับการแปลไปยันต่างประเทศอีก 13 ภาษา วรรณคดีเรื่องนี้มีความสำคัญและมีเนื้อหาเกี่ยวกับอะไร ถึงโด่งดัง เป็นที่รู้จัก และได้มาอยู่ในแบบเรียนภาษาไทย ถ้าพร้อมแล้วเราไปศึกษาประวัติความเป็นมาของวรรณคดีเรื่องนี้กันเลยค่ะ ความเป็นมา บทละครพูด เห็นแก่ลูก บทละครพูด เห็นแก่ลูก เป็นพระราชนิพนธ์ในพระบาทสมเด็จพระมงกุฎเกล้าเจ้าอยู่หัว ทรงใช้พระนามแฝงว่าพระขรรค์เพชร

การอ้างเหตุผล

บทความนี้จะทำให้น้องๆเข้าใจหลักการอ้างเหตุผลมากขึ้นและสามารถตรวจสอบได้ว่า การอ้างเหตุผล สมเหตุสมผลหรือไม่

Relative Clause

สวัสดีค่ะนักเรียนม. 3 ที่รักทุกคน วันนี้เราจะไปดู Relative clause หรือ อนุประโยคในภาษาอังกฤษ ที่ทำหน้าที่เหมือนกันกับคำคุณศัพท์ (Adjective) ซึ่งมีหน้าที่ขยายคำนามที่อยู่ข้างหน้า และจะใช้ตามหลัง Relative Pronoun เช่น who, whom, which, that, และ whose แต่สงสัยมั้ยคะว่าทำไมต้องเรียนเรื่องนี้ ลองดูตัวอย่างประโยคด้านล่างแล้วจะร้องอ๋อ Relative

วงรี

สารบัญ

วงรี

วงรี ที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิด

วงรีที่มีจุดศูนย์กลางที่ (h, k)

ตัวอย่าง

แค่ 10 นาที ก็เข้าใจได้

แนะนำ

แชร์

วิธีเขียน คำขวัญ ให้ถูกใจคนอ่าน

การใช้ Yes/No Questions และ Wh-Questions

Short question เน้นรูปอดีตโดยใช้ Did, Was, Were

เห็นแก่ลูก ศึกษาความเป็นมาบทละครพูดเรื่องแรกของไทย

การอ้างเหตุผล

Relative Clause

NockAcademy

ติดต่อ

เกี่ยวกับเรา

ความช่วยเหลือ

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1