ฟังก์ชันและกราฟของฟังก์ชัน
ฟังก์ชันและกราฟของฟังก์ชัน มีความเกี่ยวข้องกันเนื่องจากฟังก์ชันที่เราเขียนในรูป y = f(x) สามารถนำไปเขียนกราฟในระบบพิกัดฉากได้ ซึ่งกราฟในระบบพิกัดฉากก็คือ กราฟที่ประกอบไปด้วยแกน x และ แกน y
ก่อนที่เราจะเริ่มบทเรียนของฟังก์ชัน อยากให้น้องๆได้ศึกษารูปต่อไปนี้ก่อนนะคะ
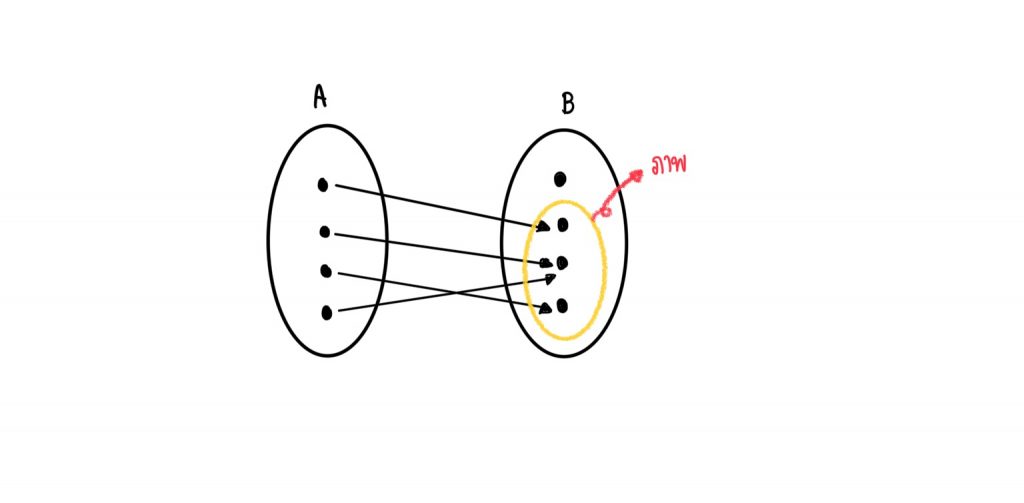
จากรูป คือการส่งสมาชิกในเซต A ไปยังสมาชิกในเซต B
เซต A จะถูกเรียกว่า โดเมน และ สมาชิกของ x แต่ละตัวใน A ที่ถูกส่งไปยัง สมาชิกบางตัวของ y เราจะเรียกสมาชิกบางตัวของ y ว่า ภาพของ x และเรียกสมาชิกในภาพว่า เรนจ์
อ่านแล้วอาจจะงงๆลองมาดูตัวอย่างกันค่ะ
ตัวอย่าง
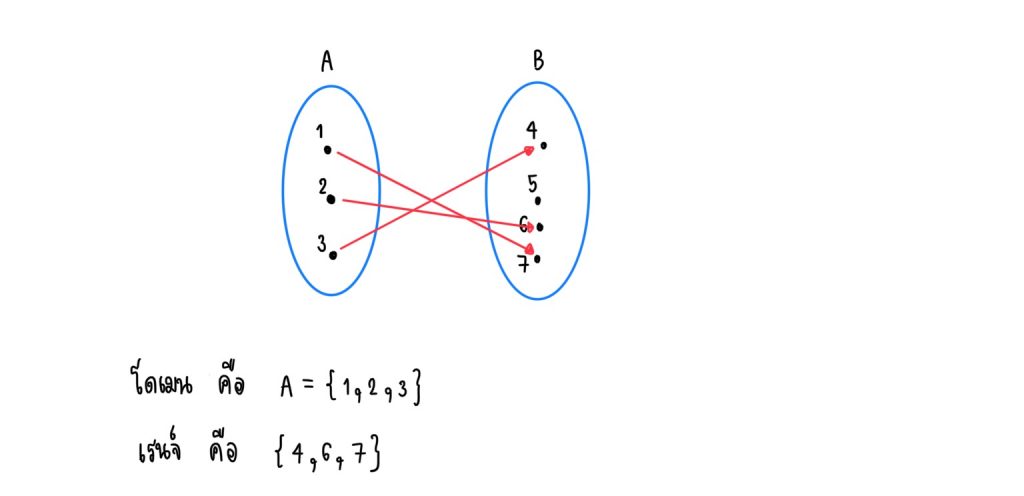
จากรูปจะเห็นว่า เรนจ์ไม่จำเป็นต้องเท่ากับ B สมาชิกบางตัวของ B ไม่จำเป็นต้องเป็นสมาชิกในเรนจ์ก็ได้
เมื่อเราเข้าใจว่าโดเมน และเรนจ์แล้วเรามาทำความเข้าใจกับฟังก์ชันและกราฟของฟังก์ชันกันต่อเลยค่ะ
ฟังก์ชัน
ฟังก์ชัน หมายถึง ความสัมพันธ์ (x, y) ใดๆ โดยที่ ถ้าตัวหน้าเหมือนกัน ตัวหลังจะต้องเหมือนกัน
แปลให้ง่ายก็คือ สมาชิกตัวหน้าจะต้องไม่เหมือนกันนั่นเองค่ะ
เช่น (1, 2) (2, 5) (-3, 4) เป็นฟังก์ชัน เพราะไม่สมาชิกของโดเมน จับคู่กับเรนจ์มากกว่า 1 ตัว
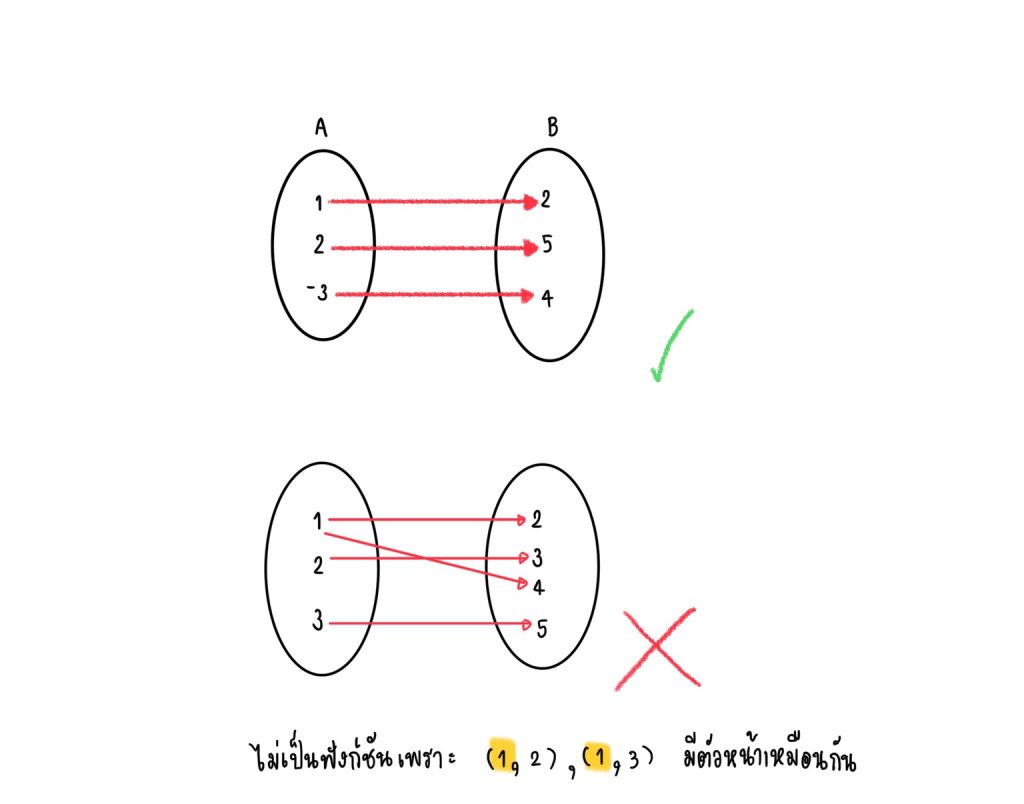
ในกรณีที่ฟังก์ชันเป็นกราฟ ให้เราลากเส้นขนาดแกน y ถ้าเกิดว่าเส้นที่เราสร้างขึ้นมาตัดกับกราฟของฟังก์ชันเกิน 1 จุด สรุปได้เลยว่ากราฟนั้นไม่เป็นฟังก์ชัน
เพราะอะไรถึงไม่เป็นฟังก์ชัน??
จากนิยามที่บอกว่า สมาชิกตัวหน้าต้องไม่เหมือนกัน
สมมติฟังก์ชันตัดกับกราฟที่เราสร้างขึ้น 2 จุด แสดงว่าค่า x 1 ค่า เกิดค่า y 2 ค่า มันก็เหมือนกับว่าสมาชิกตัวหน้ามันเหมือนกัน จึงไม่เป็นฟังก์ชัน
เช่น
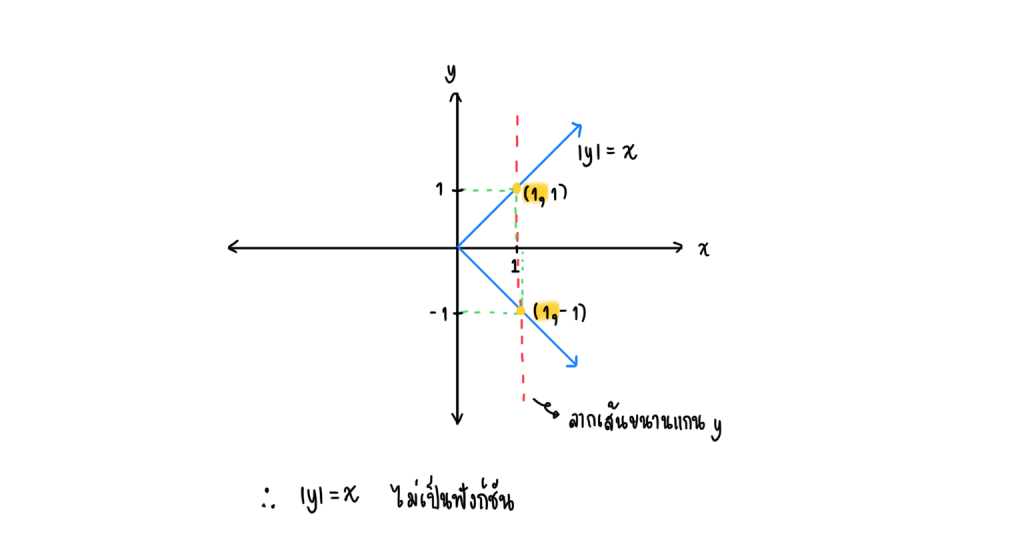
จากกราฟข้างต้นจะเห็นว่า เมื่อ x = 1 จะได้ y = 1 , -1 จะเห็นกว่า ได้ค่า y มาสองค่า กราฟนี้จึงไม่เป็นฟังก์ชันนั่นเอง
ฟังก์ชันจาก A ไป B
ให้ f เป็นฟังก์ชัน
f เป็นฟังก์ชันจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็น A และเรนจ์เป็นสับเซตของ B
เขียนแทนด้วย f : A →B
หมายความว่า สมาชิกทุกตัวใน A ทุกใช้จนหมด แต่สมาชิกใน B ไม่จำเป็นต้องถูกใช้ทุกตัว
เช่น
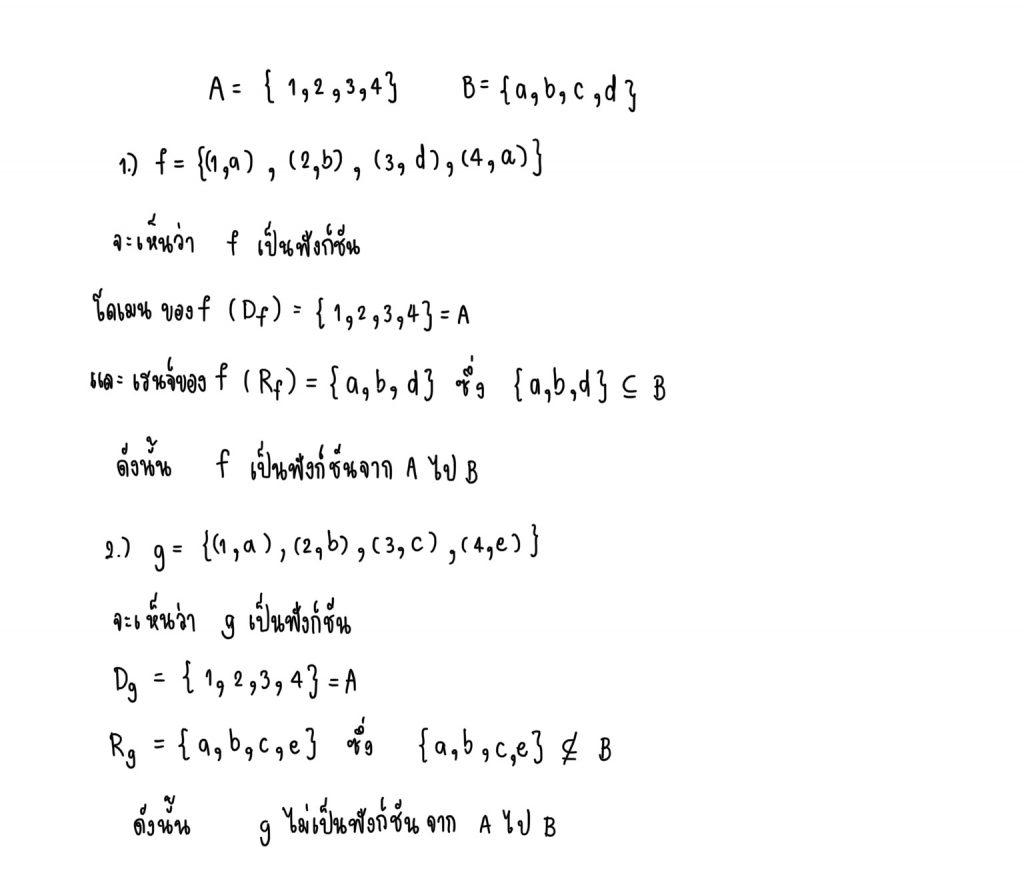
ฟังก์ชันจาก A ไปทั่วถึง B
f เป็นฟังก์ชันจาก A ไปทั่วถึง B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็น A และเรนจ์เป็น B
หมายความว่า สมาชิกทั้งในเซต A และ B ถูกใช้จนหมด
เช่น

ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B
f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันจาก A ไป B ซึ่ง เมื่อส่งสมาชิกใน A ไปแล้วจะต้องได้ค่าเรนจ์ที่แตกต่างกัน
หมายความว่า ค่า x 2 ค่า จะต้องไม่ได้ค่า y ที่ซ้ำกันนั่นเอง
เช่น

f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไปทั่วถึง B หมายความว่า f เป็นฟังก์ชันหนึ่งต่อหนึ่งและเป็นฟังก์ชันทั่วถึง
กราฟของฟังก์ชัน
กราฟของฟังก์ชัน คือ กราฟของความสัมพันธ์ที่กำหนดโดยสมการ y = f(x) ในระบบพิกัดฉากซึ่งประกอบไปด้วยจุดที่มีคู่อันดับเป็น (x, y) โดยที่ x เป็นสมาชิกในโดเมนของฟังก์ชัน และ y หรือ f(x) เป็นค่าของฟังก์ชันที่ขึ้นอยู่กับ x และเราสามารถนำฟังก์ชันนี้มาเขียนกราฟในระบบพิกัดฉากได้
อธิบายง่ายๆได้ใจความคือ x เป็นตัวแปรอิสระ และ y เป็นตัวแปรตาม
ค่าของ y จะเปลี่ยนไปตาม x นั่นเอง
เช่น y = x + 2 หรือเขียนอีกแบบคือ f(x) = x + 2
สมมติเราให้ x = 0 เราจะได้ว่า y = 0 + 2 นั่นคือ y = 2
สมมติให้ x = 1 เราจะได้ว่า y = 1 + 2 นั่นคือ y = 3
ให้ x = -2 เราจะได้ว่า y = (-2) + 2 นั่นคือ y = 0
เราจะเห็นว่า เมื่อค่า x เปลี่ยนไปค่า y ก็จะเปลี่ยนตามค่าของ x
จากการแทนค่าข้างต้น เราสามารถเขียนคู่อันดัล (x, y) ได้ดังนี้
(0, 2) , (1, 3) , (-2, 0)
และจากคู่อันดับเราสามารถนำมาเขียนกราฟได้ดังนี้
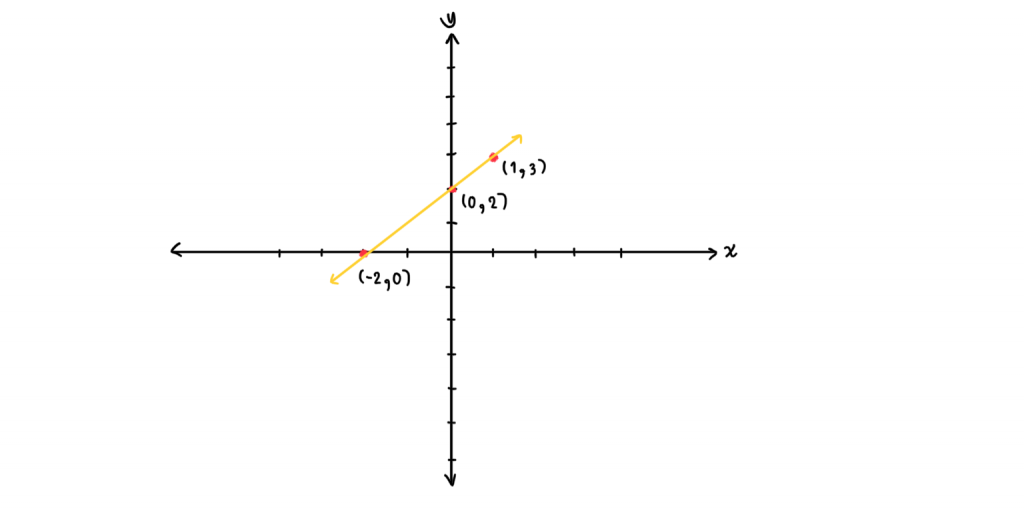
การเขียนกราฟโดยการเลื่อนขนาน
ถ้า c > 0 แล้วจะได้ว่า
- กราฟของ y = f(x) + c คือ กราฟของ y = f(x) ที่ถูกเลื่อนขึ้นไปข้างบนเป็นระยะ c หน่วย
- กราฟของ y = f(x) – c คือ กราฟของ y = f(x) ที่ถูกเลื่อนลงข้างล่างเป็นระยะ c หน่วย
- กราฟของ y = f(x + c) คือ กราฟของ y = f(x) ที่ถูกเลื่อนไปทางขวาเป็นระยะ c หน่วย
- กราฟของ y = f(x – c) คือ กราฟของ y = f(x) ที่ถูกเลื่อนไปทางซ้ายเป็นระยะ c หน่วย
ตัวอย่าง
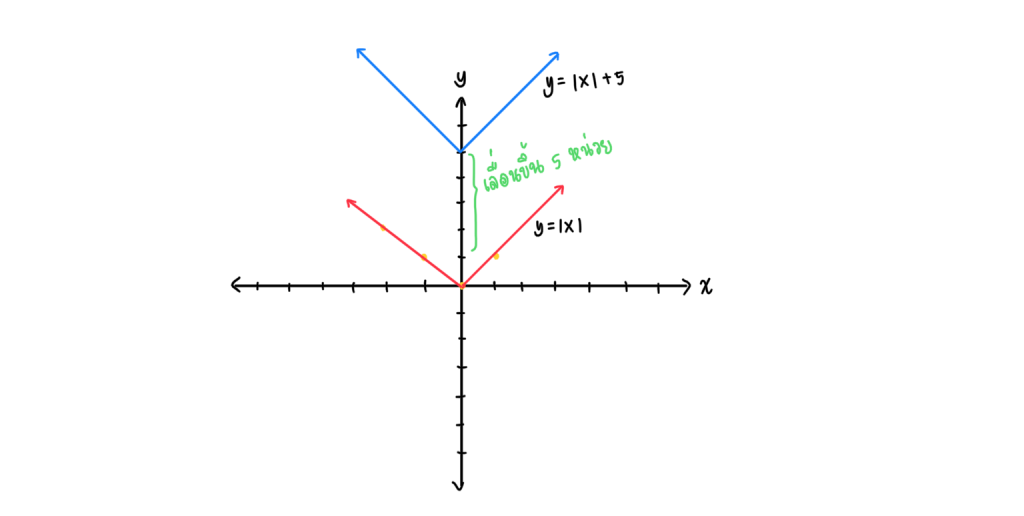
จงเขียนกราฟของ
กราฟของ คือ กราฟของ
ที่ถูกเลื่อนขึ้นข้างบน 5 หน่วยนั่นเอง
เขียนกราฟได้ดังนี้
วิดีโอเกี่ยวกับ ฟังก์ชันและกราฟของฟังก์ชัน
ฟังก์ชัน
กราฟของฟังก์ชัน


















