พาราโบลา
พาราโบลา คือเซตของจุดบนระนาบมีระยะห่างจากจุดโฟกัส (focus) เท่ากับระยะห่างจากเส้นไดเรกตริกซ์ (directrix)
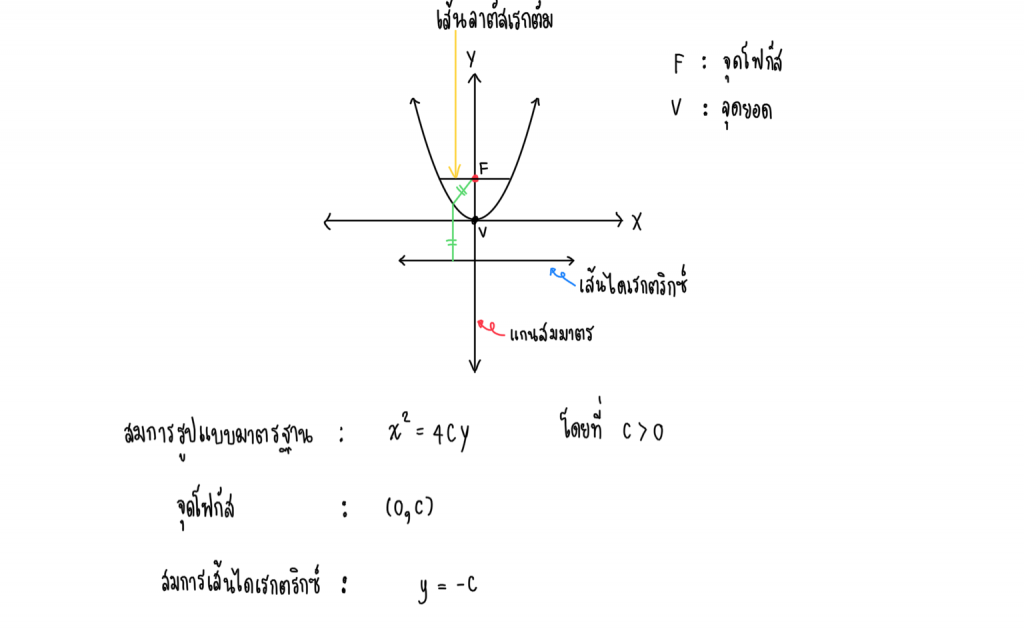
พาราโบลาที่มีจุดยอดอยู่ที่จุดกำเนิด
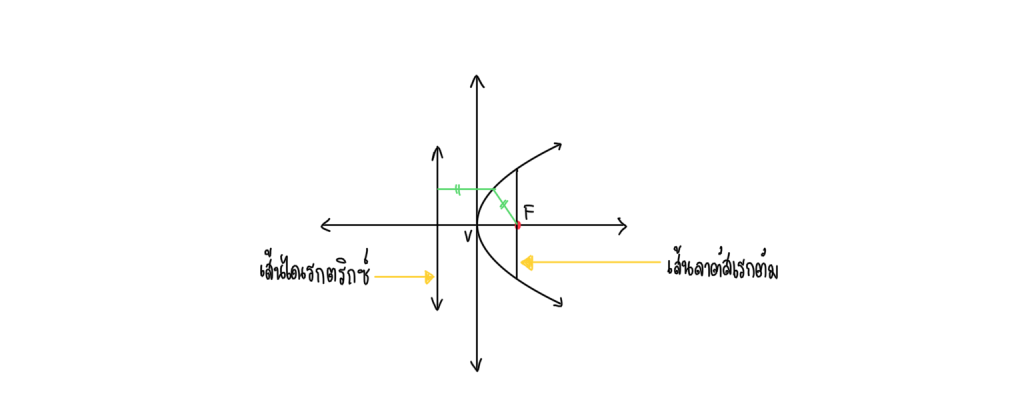
กราฟของพาราโบลาจะมีลักษณะคล้ายระฆัง ตอนม.3 น้องๆเคยเห็นทั้งพาราโบลาหงายและคว่ำแล้ว แต่ในบทความนี้น้องๆจะได้รู้จักกับพาราโบลาตะแคงซ้ายและขวา
สามารถเขียนเป็นตารางให้เข้าใจง่ายๆได้ดังนี้

ข้อสังเกต จะเห็นว่าถ้าแกนสมมาตรคือแกน y รูปแบบสมการของพาราโบลา y จะมีเลขชี้กำลังเป็น 1 สมการเส้นไดเรกตริกซ์ก็จะเกี่ยวข้องกับ y
เช่นเดียวกับแกนสมมาตรเป็นแกน x รูปแบบสมการของพาราโบลา x จะมีเลขชี้กำลังเป็น 1 สมการเส้นไดเรกตริกซ์ก็จะเกี่ยวข้องกับ x
พาราโบลาที่มีจุดยอดที่จุด (h, k)
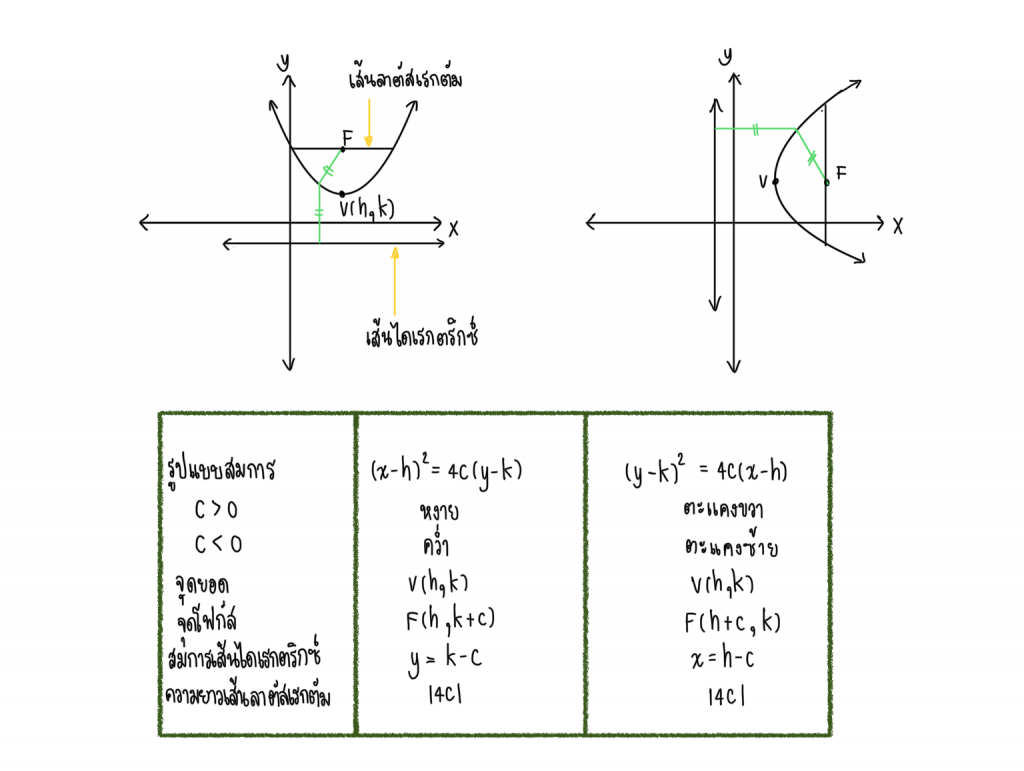
ความแตกต่างระหว่างจุดยอดที่จุดกำเนิดกับจุดยอดที่จุด (h, k)
ความแตกต่างมีแค่นิดเดียวเท่านั้นค่ะ คือ มี h และ k เข้ามาเกี่ยว น้องๆลองสังเกตดูนะคะ จากตอนแรกที่จุดยอด (0,0) จุดโฟกัส จะมีแค่ 0 กับ c (ซึ่งจะอยู่ตำแหน่งไหนก็แล้วแต่ลักษณะของกราฟ) สมการเส้นไดเรกตริกซ์ ก็จะมีแค่ c ที่เกี่ยวข้อง
แต่พอเป็น (h, k) เราแค่เพิ่มไป เช่น F(0, c) ก็กลายเป็น F(h, k+c) เป็นต้น
วิธีการจำ : พี่แนะนำให้น้องๆจำพาราโบลาที่จุดเป็น (h, k) ไปเลยนะคะ
ตัวอย่างที่ 1 จงหาสมการพาราโบลาที่มีจุดยอดที่ (0,0) และมีจุดโฟสัส (0,4) พร้อมบอกลักษณะของพาราโบลา

ตัวอย่างที่ 2 จงหาโฟกัสและเส้นไดเรกตริกซ์ของพาราโบลา

คลิปที่เกี่ยวข้องกับพาราโบลา