ฟังก์ชันเพิ่มและฟังก์ชันลด
ฟังก์ชันเพิ่มและฟังก์ชันลด สามารถตรวจสอบได้จากกราฟและนิยาม สมการหนึ่งสมการอาจจะเป็นทั้งฟังก์ชันเพิ่มและฟังก์ชันลดขึ้นอยู่กับรูปแบบของกราฟและสมการ
บทนิยาม
ให้ f เป็นฟังก์ชันที่ส่งจากโดเมนของฟังก์ชันไปยังจำนวนจริง โดยที่ A เป็นสับเซตของจำนวนจริง และ A เป็นสับเซตของโดเมน จะบอกว่า
f เป็นฟังก์ชันเพิ่มบนเซตเซต A ก็ต่อเมื่อ สำหรับ
และ
ใดๆใน A ถ้า
<
แล้ว f(
) < f(
)
f เป็นฟังก์ชันลดบนเซต A ก็ต่อเมื่อ สำหรับ
และ
ใดๆใน A ถ้า
<
แล้ว f(
) > f(
)
อธิบายนิยาม
f เป็นฟังก์ชันเพิ่ม เมื่อค่า x เพิ่มขึ้น ค่า y เพิ่มขึ้น
f เป็นฟังก์ชันลด เมื่อค่า x เพิ่มขึ้น แต่ค่า y ลดลง
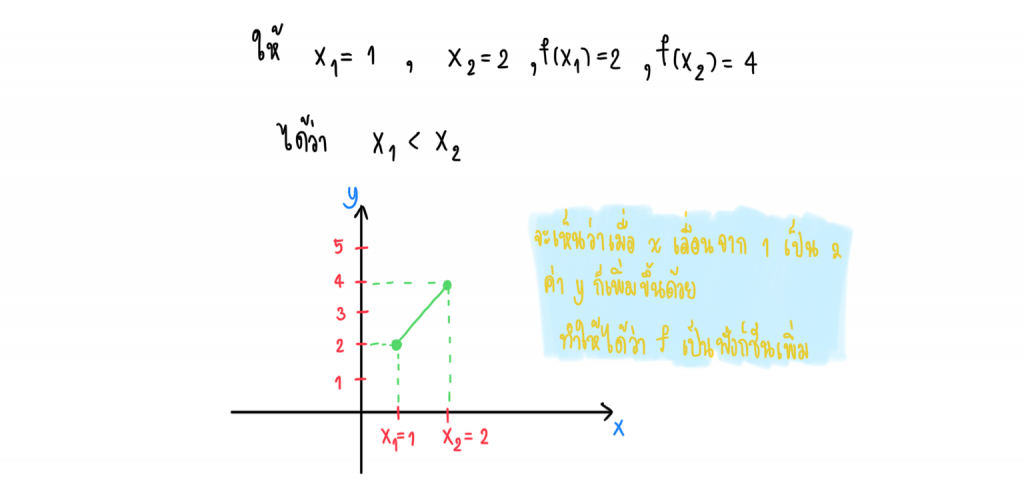
เมื่อ เราหยิบ x ใดๆ มาสองตัว สมมติให้เป็น 1 และ 2 และสมมติให้ f(1) = 2 , f(2) = 4 จะเห็นว่า f(1) < f(2) เราจะสรุปว่า f เป็นฟังก์ชันเพิ่มบนช่วง [1, 2]
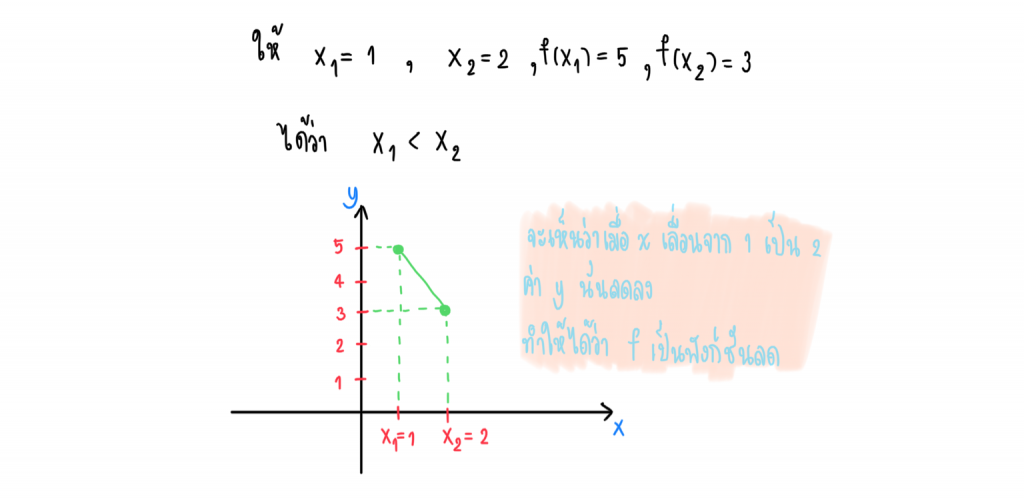
ถ้าสมมติให้ f(1) = 5 , f(2) = 3 จะเห็นว่า f(1) > f(2) เราจะสรุปว่า f เป็นฟังก์ชันลดบนช่วง [1, 2]
วิธีการตรวจสอบฟังก์ชันเพิ่มและฟังก์ชันลด
ตรวจสอบโดยใช้นิยาม
f(x) = 4x – 3
จะตรวจสอบว่า f เป็นฟังก์ชันเพิ่มหรือลดบน
วิธีทำ ให้ ,
เป็นสมาชิกใน
โดยที่
<

g(x) = -2x + 5
จะตรวจสอบว่า g เป็นฟังก์ชันเพิ่มหรือลดบน (หรือ (0, ∞))
วิธีทำ ให้ ,
เป็นสมาชิกใน
โดยที่
<

สาเหตุที่ต้องคูณหรือบวกด้วยจำนวนจริงบางตัว เพราะว่าเราอยากได้รูปแบบของ f(x) และ g(x) เนื่องจากเราไม่สามารถเริ่มพิจารณาตั้งแต่สมการที่เต็มรูปแบบได้ เราจึงต้องค่อยๆเริ่มจากสิ่งที่เรามี นั่นก็คือ <
แล้วค่อยบวกหรือคูณด้วยจำนวนจริงสักตัว เพื่อให้ได้รูปแบบของสมการตามที่โจทย์กำหนดมา
ตรวจสอบโดยพิจารณาจากกราฟ
f(x) = x² + 2x เป็นฟังก์ชันเพิ่มหรือลดบน (-∞, 0) และเป็นฟังก์ชันเพิ่มหรือลดบนช่วง (0, ∞)
จาก f(x) = x² + 2 เป็นกราฟของพาราโบลาหงายที่มีจุดวกกลับที่จุด (0, 2)
วาดกราฟได้ดังนี้
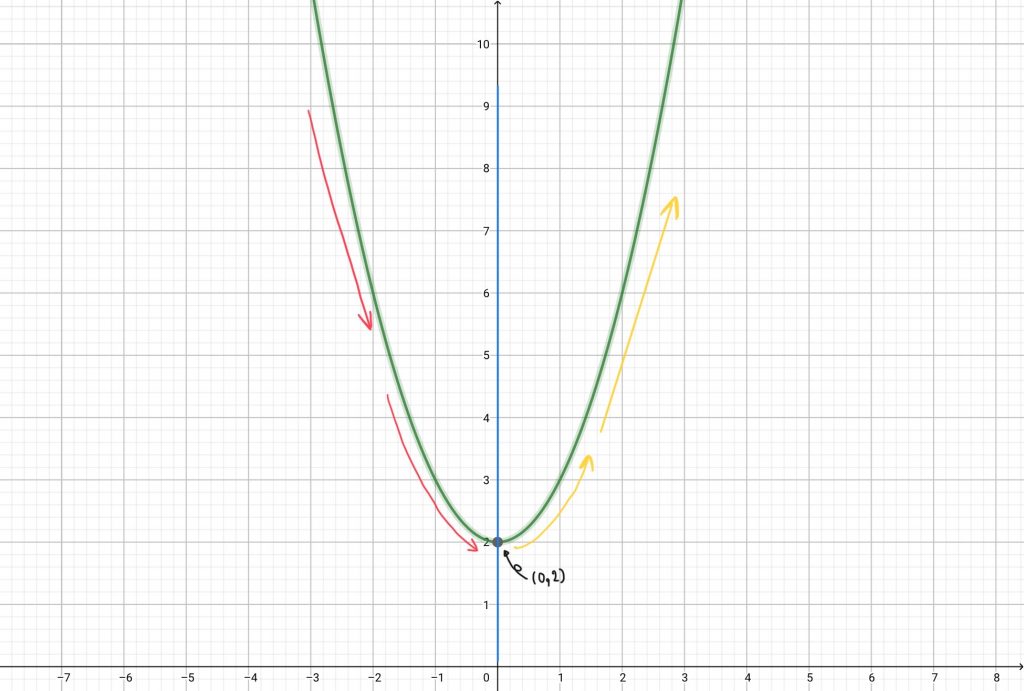
จะเห็นว่าเมื่อเราแบ่งกราฟเป็นสองช่วง คือ (-∞, 0) และ (0, ∞)
พิจารณา (-∞, 0) จะเห็นว่า ค่าของ y นั้นลดลงในขณะที่ค่า x เพิ่มขึ้น ดังนั้น f เป็นฟังก์ชันลดบนช่วง (-∞, 0)
พิจารณา (0, ∞) จะเห็นว่าค่าของ y เพิ่มขึ้นและค่า x ก็เพิ่มขึ้นด้วย ดังนั้น f เป็นฟังก์ชันเพิ่มบนช่วง (0, ∞)
——————————————————————————————————————————————————————
พิจารณากราฟต่อไปนี้ แล้วบอกว่า f และ g เป็นฟังก์ชันเพิ่มช่วงไหน และเป็นฟังก์ชันลดช่วงไหน
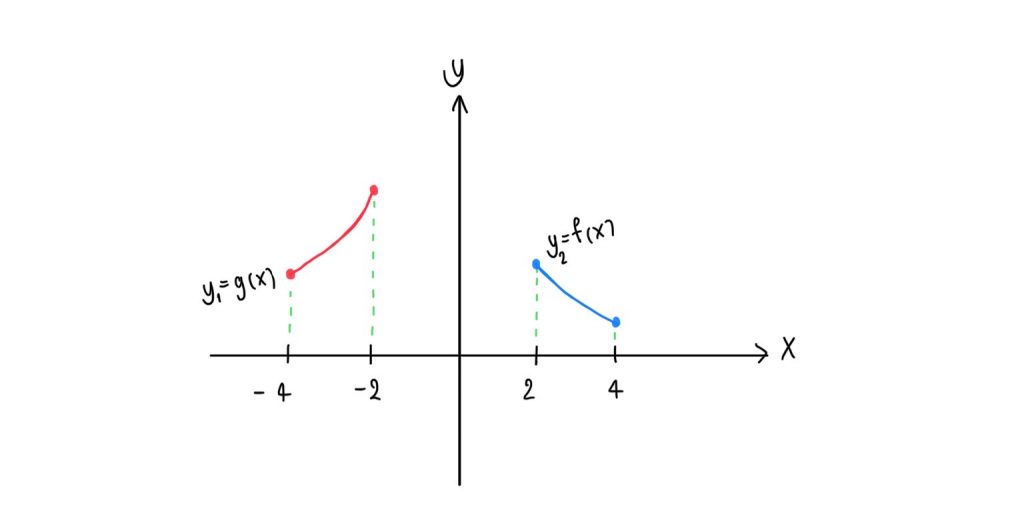
จากกราฟจะได้ว่า g(x)เป็นฟังก์ชั่นเพิ่มบนช่วง [-4, -2] เพราะ เมื่อ x เพิ่มขึ้น ค่า y ก็เพิ่มขึ้นด้วย
และ f(x) เป็นฟังก์ชันลดบนช่วง [2, 4] เพราะเมื่อ x เพิ่มขึ้น ค่า y ลดลง