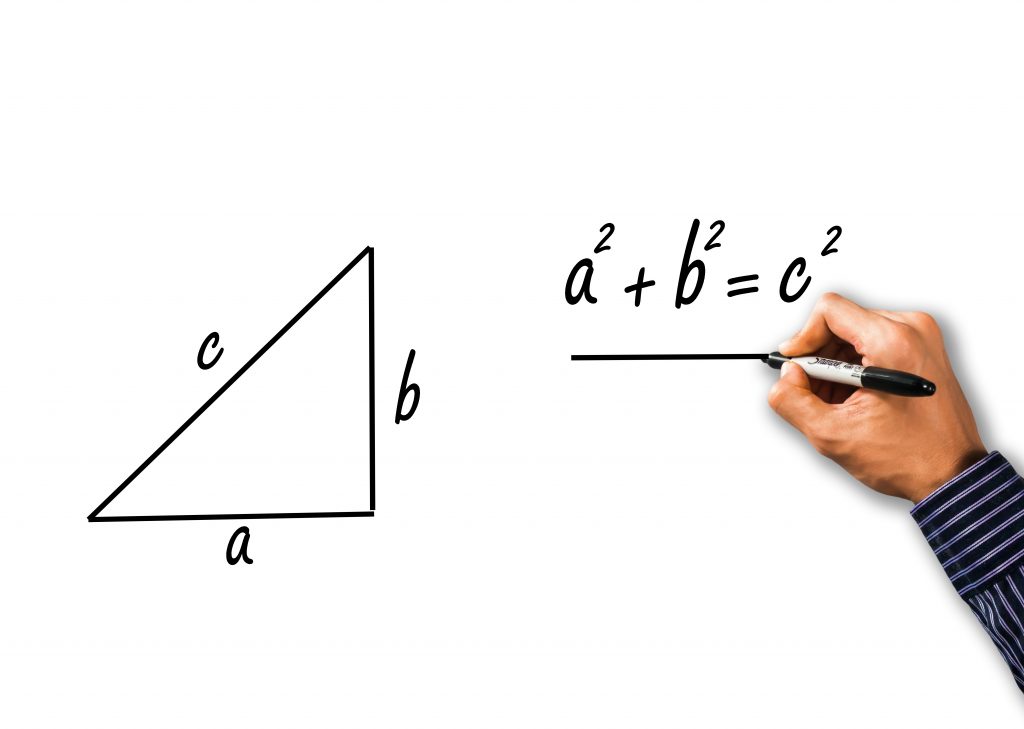บทกลับของทฤษฎีบทพีทาโกรัส

ในบทความนี้เราจะได้เรียนรู้ความหมายและหลักการในการแสดงเหตุและผลของบทกลับของทฤษฎีบทพีทาโกรัส

tucksaga

คณิตศาสตร์, คณิตศาสตร์ ม.2, ม.2

Add LINE friends for one click to find article.

จะเห็นได้ว่าบทกลับของทฤษฎีบทพีทาโกรัสเป็นการนําผลของทฤษฎีบทพีทาโกรัสมาเป็นเหตุและนําเหตุมาเป็นผลนั่นเอง เพื่อประยุกต์ใช้ในรูปสามเหลี่ยมแต่ละลักษณะนั่นเอง

บทกลับของทฤษฎีบทพีทาโกรัส

บทกลับของทฤษฎีบทพีทาโกรัสกล่าวว่า “สำหรับรูปสามเหลี่ยมใดๆ ถ้ากำลังสองของความยาวของด้านด้านหนึ่งเท่ากับผลบวกของกำลังสองของความยาวของด้านอีกสองด้านแล้วรูปสามเหลี่ยมนั้นเป็นสามเหลี่ยมมุมฉาก”

โดยบทกลับของทฤษฎีบทพีทาโกรัสเป็นการนำผลของทฤษฎีบทพีทาโกรัสมาเป็นเหตุและนำเหตุมาเป็นผล ดังนั้น

เหตุ: มีรูปสามเหลี่ยมรูปหนึ่ง เป็นรูปสามเหลี่ยมมุมฉาก

ผล : กำลังสองของความยาวของด้านตรงข้ามมุมฉาก เท่ากับ ผลบวกของกำลังสองของความยาวของด้านประกอบมุมฉากของรูปสามเหลี่ยม

เมื่อนำผลข้างต้นมาเป็นเหตุ และเหตุมาเป็นผล ก็จะได้บทกลับของทฤษฎีบทพีทาโกรัส ดังนี้

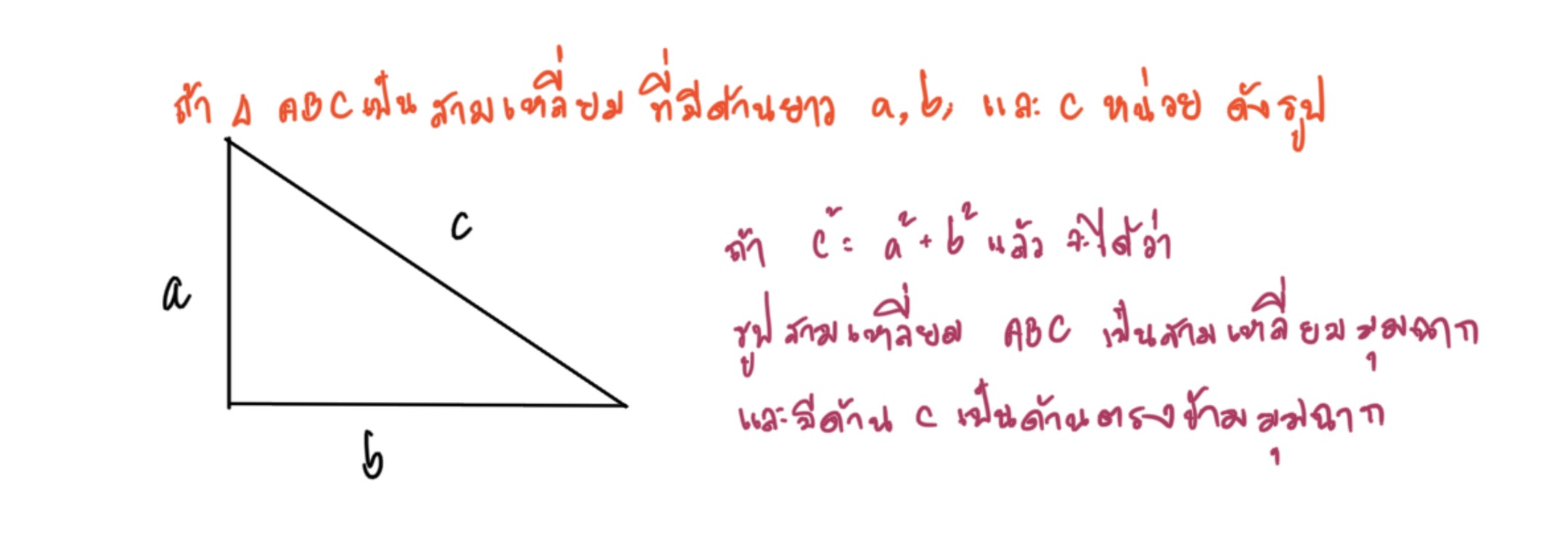
ตัวอย่างที่ 1

กำหนดความยาวของด้านทั้งสามของรูปสามเหลี่ยมให้ให้แสดงว่ารูปสามเหลี่ยมนั้นเป็นรูปสามเหลี่ยมมุมฉากหรือไม่

1) 7, 9, 11 2) 8, 15, 17

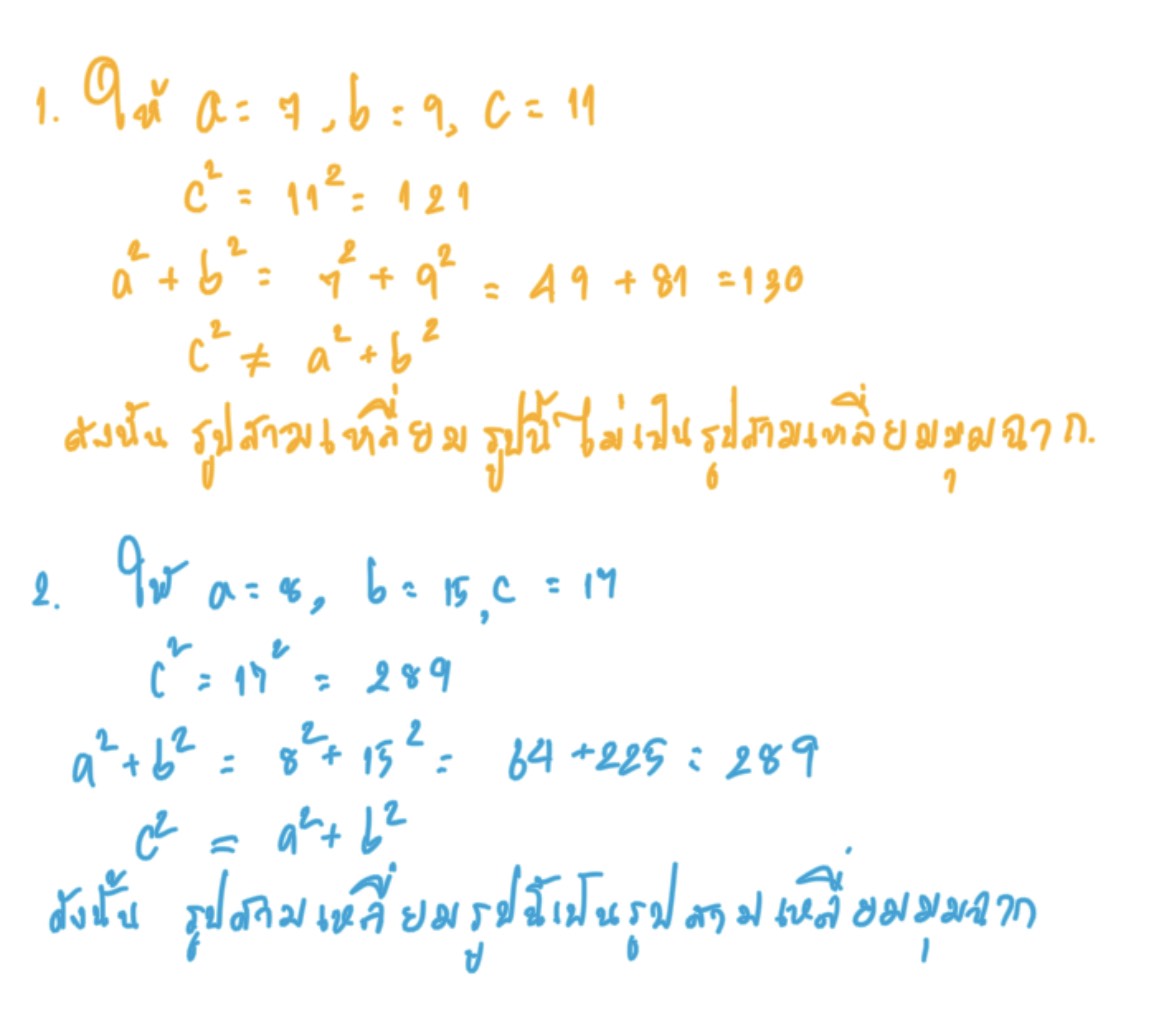
ในกรณีที่โจทย์กำหนดความยาวให้ 3 ด้าน และถามว่านำมาประกอบกันเป็นรูปสามเหลี่ยมมุมฉากหรือไม่ ถ้าใช่ยังสามารถตรวจสอบต่อไปได้อีกว่าเป็นรูปสามเหลี่ยมอะไรโดยพิจารณาให้ ดังนี้

และความยาวของด้านทั้งสามต้องสัมพันธ์กันดังนี้คือ c < a + b มิฉะนั้นจะนำมาสร้างรูปสามเหลี่ยมไม่ได้

ตัวอย่างที่ 2

กำหนดความยาวของด้านให้สามด้าน นำมาสร้างรูปสามเหลี่ยมจะได้รูปสามเหลี่ยมอะไร

1) 2, 3,6 2) 3, 4, 5 3) 4 5, 6 4) 5, 6, 8

คลิปตัวอย่างเรื่องบทกลับของทฤษฎีบทพีทาโกรัส

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

การอ่านบทร้อยกรอง กาพย์และโคลงอ่านอย่างไรให้ไพเราะ

น้อง ๆ คงจะรู้การคำประพันธ์อย่างกาพย์และโคลงกันอยู่แล้วใช่ไหมคะ เพราะวรรณคดีไทยหลาย ๆ เรื่องที่เราเรียนกันมา ก็ใช้กาพย์และโคลงแต่งกันเสียส่วนใหญ่ และหลังจากที่ได้เรียนลักษณะการแต่งกาพย์กับโคลงสี่สุภาพ ให้ไพเราะกันไปแล้ว จะแต่งอย่างเดียวโดยไม่อ่านให้ถูกต้องก็ไม่ได้ใช่ไหมล่ะคะ ดังนั้นบทเรียนวันนี้จะพาร้อง ๆ ไปเรียนรู้เรื่อง การอ่านบทร้อยกรอง กันบ้าง ว่ามีวิธีอ่านอย่างไรให้ถูกต้องและไพเราะ ไปเรียนรู้พร้อม ๆ กันเลยค่ะ การอ่านบทร้อยกรอง การอ่านบทร้องกรอง ประเภทกาพย์

รากที่สาม

ในบทตวามนี้เราจะได้เรียนรู้การหารากที่สามของจำนวนจริงใดๆ ซึ่งทำได้หลายวิธีเช่นเดียวกับการหารากที่สอง อาจใช้การแยกตัวประกอบ การประมาณ การเปิดตาราง และการใช้เครื่องคำนวณ แต่เนื่องจากการประมาณเป็นวิธีที่ยุ่งยาก ในที่นี้จึงจะกล่าวเฉพาะการหารากที่สามโดยการแยกตัวประกอบ การเปิดตาราง และการใช้เครื่องคำนวณ

ดีเทอร์มิแนนต์

ดีเทอร์มิแนนต์ ดีเทอร์มิแนนต์ (Determinant) คือ ค่าของตัวเลขที่สอดคล้องกับเมทริกซ์จัตุรัส ถ้า A เป็นเมทริกซ์จัตุรัส จะเขียนแทนดีเทอร์มิแนนต์ของ A ด้วย det(A) หรือ โดยทั่วไปการหาค่าดีเทอร์มิแนนต์ที่เจอในข้อสอบจะไม่เกินเมทริกซ์ 3×3 เพราะถ้ามากกว่า 3 แล้ว จะเริ่มมีความยุ่งยาก **ค่าของดีเทอร์มิแนนต์จะเป็นจำนวนจริงและมีเพียงค่าเดียวเท่านั้นที่จะสอดคล้องกับเมทริกซ์จัตุรัส เช่น เมทริกซ์ B ก็จะมีค่าดีเทอร์มิแนนต์เพียงค่าเดียวเท่านั้น**

สถิติ (ค่ากลางของข้อมูล/การกระจายของข้อมูล)

บทความนี้ได้รวบรวมความรู้เรื่อง ค่ากลางของข้อมูลและการกระจายของข้อมูล ซึ่งค่ากลางของข้อมูลจะประกอบด้วย ค่าเฉลี่ยเลขคณิต มัธยฐาน และฐานนิยม ส่วนการวัดการกระจายของข้อมูลจะศึกษาในเรื่องการหาส่วนเบี่ยงเบนมาตรฐาน ซึ่งน้องๆสามารถทบทวน การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ ได้ที่ ⇒⇒ การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ ⇐⇐ หมายเหตุ ค่าเฉลี่ยในทางคณิตศาสตร์มีหลายชนิด แต่ที่นิยมใช้คือค่าเฉลี่ยเลขคณิต การวัดค่ากลางของข้อมูล เป็นการหาค่ากลางมาเป็นตัวแทนของข้อมูลแต่ละชุด ซึ่งมีวิธีการหาได้หลายวิธีที่นิยมกัน ได้แก่ ค่าเฉลี่ยเลขคณิต มัธยฐาน ฐานนิยม ค่าเฉลี่ยเลขคณิต (Arithmetic

กัณฑ์มัทรี ศึกษาตัวบทและข้อคิดของกัณฑ์ที่ 9 ในมหาชาติชาดก

กัณฑ์ หมายถึง คำเทศน์ หรือตอนหนึ่ง ๆ ของเทศน์เรื่องยาว นับเป็นลักษณนามของเทศน์ ในมหาชาติชาดก เราได้เรียนรู้เกี่ยวกับความเป็นมากันไปแล้วว่ามีทั้งหมด 13 กัณฑ์ รวมถึงเรื่องย่อของกัณฑ์มัทรี ซึ่งเป็นกัณฑ์ที่ 9 มีความเชื่อว่าถ้าใครได้ฟังเทศน์มหาชาติทั้ง 13 กัณฑ์ของมหาชาติชาดก ก็จะทำให้ขึ้นสวรรค์ นอกจากนี้หากบูชากัณฑ์ต่าง ๆ ก็จะได้ผลที่ดีแก่ตัวเอง ผู้ที่บูชากัณฑ์มัทรี จะทำให้เป็นผู้มั่งคั่ง สมบูรณ์ไปด้วยทรัพย์สมบัติ เป็นผู้มีอายุยืนยาว

เรียนรู้เกี่ยวกับการบอกเวลา

Hi guys! สวัสดีค่ะนักเรียนชั้น ม.1 ที่น่ารักทุกคน วันนี้เราจะไป เรียนรู้เกี่ยวกับการบอกเวลา กันค่ะ ถ้าพร้อมแล้วก็ไปลุยกันเลย Let’s go! การแบ่งประเภท ในบทเรียนนี้ครูขอยกตัวอย่างการบอกเวลาที่นิยมใช้กันโดยทั่วไปใน 2 รูปแบบ ตามที่มาของ Native English หรือ ภาษาอังกฤษของเจ้าของภาษา นะคะ ดังตัวอย่างดังต่อไปนี้

บทกลับของทฤษฎีบทพีทาโกรัส

สารบัญ

บทกลับของทฤษฎีบทพีทาโกรัส

ตัวอย่างที่ 1

ตัวอย่างที่ 2

คลิปตัวอย่างเรื่องบทกลับของทฤษฎีบทพีทาโกรัส

แค่ 10 นาที ก็เข้าใจได้

แนะนำ

แชร์

การอ่านบทร้อยกรอง กาพย์และโคลงอ่านอย่างไรให้ไพเราะ

รากที่สาม

ดีเทอร์มิแนนต์

สถิติ (ค่ากลางของข้อมูล/การกระจายของข้อมูล)

กัณฑ์มัทรี ศึกษาตัวบทและข้อคิดของกัณฑ์ที่ 9 ในมหาชาติชาดก

เรียนรู้เกี่ยวกับการบอกเวลา

NockAcademy

ติดต่อ

เกี่ยวกับเรา

ความช่วยเหลือ

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1