ตัวผกผันของความสัมพันธ์

supanaree

คณิต ม.4 พื้นฐาน, คณิตศาสตร์, คณิตศาสตร์ ม.4, ม.4

Add LINE friends for one click to find article.

ตัวผกผันของความสัมพันธ์

ตัวผกผันของความสัมพันธ์ r คือความสัมพันธ์ใหม่ที่เกิดจากการสลับตำแหน่งของสมาชิกตัวหน้ากับสมาชิกตัวหลังของคู่อันดับทุกคู่ในความสัมพันธ์ r เขียนแทนด้วย $r^{-1}$ ซึ่ง $r^{-1}$ = {(y, x) : (x, y ) ∈ r}

เช่น r = {(1, 2), (3, 4), (5, 6)}

จากคู่อันดับของความสัมพันธ์ r จะได้ว่า $D_r$ = {1, 3, 5} และ $R_r$ = {2, 4, 6}

และจะได้ตัวผกผันของ r คือ $r^{-1}$ = {(2, 1), (4, 3), (6, 5)}

และจาก $r^{-1}$ จะได้ว่า $D_{r^{-1}}$ = {2, 4, 6} = $R_r$ และ $R_{r^{-1}}$ = {1, 3, 5} = $D_r$

จะเห็นว่า โดเมนของตัวผกผันของความสัมพันธ์ r คือ เรนจ์ของความสัมพันธ์ r และ เรนจ์ของตัวผกผันของความสัมพันธ์ r คือ โดเมนของความสัมพันธ์ r

ตัวอย่าง

1.) ให้ r = {(x, y) ∈ $\mathbb{R}\times \mathbb{R}$ : y = 2x +1} จงหา $r^{-1}$

จาก $r^{-1}$ = {(y, x) : (x, y ) ∈ r}

จะได้ $r^{-1}$ = {(y, x) ∈ $\mathbb{R}\times \mathbb{R}$ : y = 2x +1}

หรือสามารถเขียนได้อีกแบบ คือ $r^{-1}$ = {(x, y) ∈ $\mathbb{R}\times \mathbb{R}$ : x = 2y + 1} (เปลี่ยน x เป็น y เปลี่ยน y เป็น x คู่อันดับเหมือนเดิม)

จัดสมการใหม่ จาก x = 2y+1 เป็น $y=\frac{x-1}{2}$

ดังนั้น จะได้ว่า $r^{-1}$ = {(x, y) ∈ $\mathbb{R}\times \mathbb{R}$ : $y=\frac{x-1}{2}$ } (รูปแบบที่นิยมเขียนกันมากที่สุด)

2.) ให้ r = {(x, y) ∈ $\mathbb{R}\times \mathbb{R}$ : $y=\sqrt{x-2}$ } จงหา $r^{-1}$ พร้อมวาดกราฟของ $r^{-1}$

นำความสัมพันธ์ดังกล่าวมาวาดกราฟได้ดังนี้

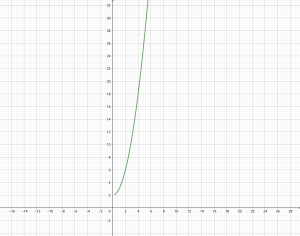
3.) ให้ r = {(x, y) ∈ $\mathbb{R}\times \mathbb{R}$ : $y=\frac{2}{x-5}$ } หาตัวผกผันของ r

จาก $r^{-1}$ = {(y, x) : (x, y ) ∈ r}

เขียนแบบที่1 หน้าเปลี่ยน >> หลัง(เงื่อนไข)เหมือนเดิม

จะได้ $r^{-1}$ = {(y, x) ∈ $\mathbb{R}\times \mathbb{R}$ : $y=\frac{2}{x-5}$ }

เขียนแบบที่ 2 หน้าเหมือนเดิม >> หลัง(เงื่อนไข)เปลี่ยน

จะได้ $r^{-1}$ = {(x, y) ∈ $\mathbb{R}\times \mathbb{R}$ : $x=\frac{2}{y-5}$ }

วิดีโอตัวผกผันของความสัมพันธ์

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

อนุกรมเลขคณิต

อนุกรมเลขคณิต อนุกรมเลขคณิต คือการนำลำดับเลขคณิตแต่ละพจน์มาบวกกัน โดย เขียนแทนด้วย จากบทความ “สัญลักษณ์การบวก” ซึ่งเป็นการลดรูปการเขียนจำนวนหลายจำนวนบวกกัน ในบทความนี้จะพูดถึงการบวกของลำดับเลขคณิต การหาผลบวก สูตรสำหรับการหาผลบวกเลขคณิต สูตรอนุกรมเลขคณิต สูตรของอนุกรมเลขคณิตมีอยู่ 2 สูตร ดังนี้ 1) โดยที่ d คือ ผลต่างร่วม 2) โดยจะใช้สูตรนี้ก็ต่อเมื่อรู้ค่า

เตรียมสอบเข้า ม.1 โรงเรียนสวนกุหลาบวิทยาลัย

เตรียมสอบเข้าม.1 โรงเรียนสวนกุหลาบวิทยาลัย สวัสดีค่ะน้อง ๆ วันนี้มาพบกับพี่แอดมินและ Nock Academy อีกเช่นเคย ซึ่งเรายังคงอยู่กับหัวข้อของการเตรียมสอบเข้าม.1กันนะคะ วันนี้แอดมินจะพาน้อง ๆ ไปรู้จักกับโรงเรียนสวนกุหลาบวิทยาและการเตรียมตัวสอบเข้าในระดับชั้นม.1ของโรงเรียนแห่งนี้กันค่ะ ก่อนอื่นแอดมินต้องขอกล่าวประวัติคร่าว ๆ ของโรงเรียนให้ทุกคนได้รู้จักกันก่อนนะคะ โรงเรียนสวนกุหลาบวิทยาเป็นโรงเรียนชายล้วนที่ก่อตั้งขึ้นมาในสมัยพระบาทสมเด็จพระจุลจอมเกล้าเจ้าอยู่หัว (รัชกาลที่ 5) ถือเป็นโรงเรียนรัฐบาลแห่งแรกของประเทศไทย ที่มีความโดดเด่นในเรื่องของวิชาการ ภาษาและความเป็นผู้นำ โดยศิษย์เก่าที่สำเร็จการศึกษามาจากโรงเรียนสวนกุหลาบวิทยาลัยแห่งนี้หลายคนเป็นผู้ที่มีชื่อเสียงและประสบความเร็จจึงทำให้ชื่อเสียงของโรงเรียนสวนกุหลาบวิทยาลัยนั้นเป็นที่รู้จักกันอย่างแพร่หลายในสังคมไทยมาอย่างยาวนาน หลักสูตรสวนกุหลาบวิทยาลัย ม.ต้น ในปัจจุบันโรงเรียนสวนกุหลาบวิทยาลัยได้มีการปรังปรุงและพัฒนาหลักสูตรให้มีความเท่าทันสังคมไทยในปัจจุบันมากยิ่งขึ้น

รู้ไว้ไม่พลาด! คำที่มักเขียนผิด ในภาษาไทย มีคำว่าอะไรบ้าง?

ปัจจุบัน ปัญหาเรื่องการสะกดคำในภาษาไทยถือเป็นปัญหาใหญ่หลัก ๆ ของเด็กทุกคนในสมัยนื้ เนื่องจากว่าโลกของเรามีการพัฒนาไปอย่างรวดเร็ว ภาษามีการเปลี่ยนแปลงไปตามยุคสมัย เพื่อให้สะดวกต่อการใช้ในโซเชี่ยลมีเดียพูดคุยกับเพื่อน โดยการจะตัดคำให้สั้นลงหรือเปลี่ยนตัวสะกด ลดการใช้ตัวการันต์ ทำให้เมื่อต้องมาเขียนคำที่ถูกต้องกันจริง ๆ ก็มีเด็ก ๆ หลายคนที่สะกดผิด ไม่รู้ว่าคำที่ถูกต้องเป็นอย่างไร น้อง ๆ อยากลองสำรวจตัวเองดูกันไหมคะว่าคำในภาษาไทยที่เราใช้กันอยู่ทุกวันนี้ เราเขียนถูกกันมากน้อยแค่ไหน อยากถามรู้แล้วเราไปดูเรื่อง คำที่มักเขียนผิด พร้อมกันเลยค่ะ การเขียนสะกดคำ

คติธรรมในสำนวนไทย

คติธรรม หมายถึง ธรรมที่เป็นแบบอย่าง เป็นวัฒนธรรมที่เกี่ยวกับหลักการดำเนินชีวิตซึ่งได้มาจากหลักธรรมทางพระพุทธศาสนาหรืออาจเรียกได้ว่าเป็นวัฒนธรรมทางจิตใจอย่างหนึ่งที่คนไทยให้ความสำคัญอย่างมากและมักจะถูกสอดแทรกอยู่ในสื่อต่าง ๆ เพื่อปลูกฝังเด็กรุ่นใหม่ให้มีคติธรรมประจำใจ ไม่ว่าจะเป็นนิทานหรือสำนวนไทย สำหรับบทเรียนในวันนี้เราจะพาน้อง ๆ ไปเรียนรู้เรื่อง คติธรรมในสำนวนไทย มาดูกันค่ะว่าจะมีอะไรบ้าง สำนวนที่เกี่ยวกับคติธรรม สำนวนไทยถือเป็นภูมิปัญญาในการใช้ภาษาไทยอีกรูปแบบหนึ่ง เป็นถ้อยคำที่มิได้มีความหมายตรงไปตรงมาตามตัวอักษร หรือแปลตามรากศัพท์ แต่เป็นถ้อยคำที่มีความหมายเป็นอย่างอื่น ชวนให้ผู้อ่านได้คิด มีรูปแบบการใช้ภาษาที่ต้องผ่านการเรียบเรียงถ้อยคำ การรวมข้อความยาว ๆ ให้สั้น โดยนำถ้อยคำเพียงไม่กี่คำมาเรียงร้อย