ในการเขียนกราฟแสดงความสัมพันธ์ปริมาณเชิงเส้นกรณีที่กราฟมีลักษณะเป็นจุด เพื่อดูแนวโน้มของความสัมพันธ์เรานิยมเขียนต่อจุดเหล่านั้นให้เป็นส่วนหนึ่งของเส้นตรง

กราฟแสดงความสัมพันธ์ปริมาณเชิงเส้น

การเขียนแสดงความสัมพันธ์ระหว่างปริมาณสองชุดโดยใช้กราฟบนระนาบในระบบพิกัดฉากมาแล้ว มีทั้งกราฟที่เป็นเส้นตรงและไม่เป็นเส้นตรงให้พิจารณาสถานการณ์ต่อไปนี้

กราฟแสดงความสัมพันธ์ของปริมาณการซื้อขาย

ตัวอย่าง ตั้วและแต้วต้องการหารายได้พิเศษช่วงปิดเทอม จึงไปรับเสื้อมาช่วยกันขาย วันหนึ่งทั้งตัวและแต้วต่างก็ขายเสื้อได้จำนวนหนึ่ง แต่รวมกันแล้วเป็นจำนวนเสื้อทั้งหมด 9 ตัว จงเขียนกราฟแสดงความสัมพันธ์ระหว่างจำนวนเสื้อที่เป็นไปได้ซึ่งตั้วและแต้วขายได้

ถ้าให้ x แทนจำนวนเสื้อที่ตัวขายได้เป็นตัว

      y แทนจำนวนเสื้อที่แต้วขายได้เป็นตัว

จำนวนเสื้อที่แต่ละคนขายได้จะต้องเป็นจำนวนนับที่รวมกันเป็น 9 ดังตาราง

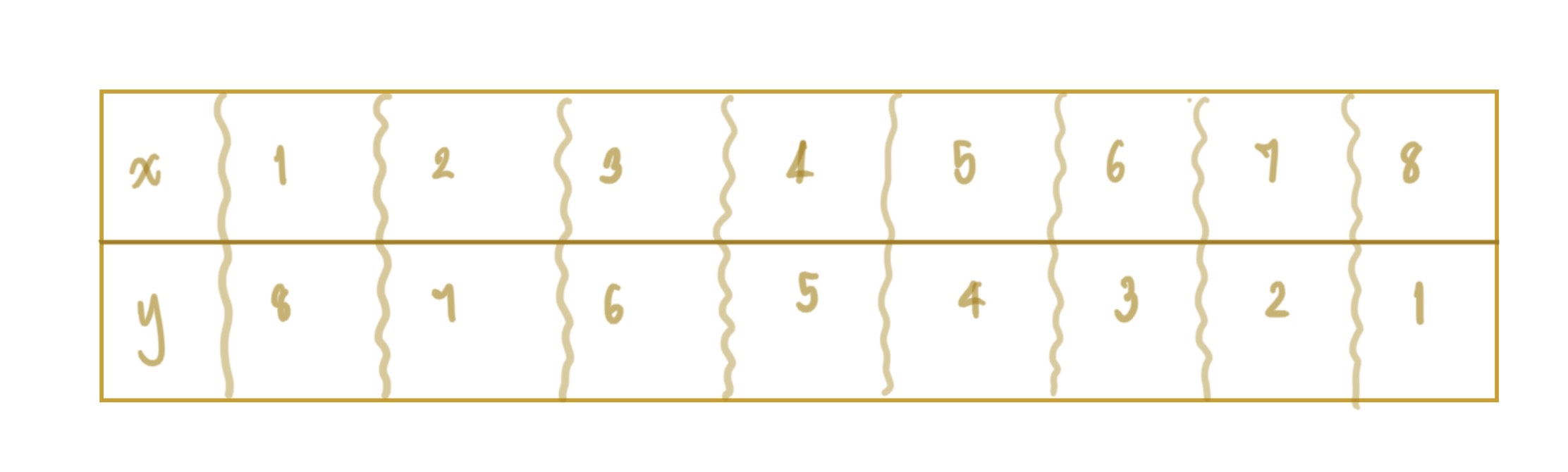
จากตารางเขียนคู่อันดับ (x, y) แสดงความสัมพันธ์ระหว่างจำนวนเสื้อที่ตัวและแต้วแต่ละคนขายได้ ได้ดังนี้ (1, 8), (2, 7), (3, 6), (4, 5), (5, 4), (6, 3), (7, 2), (8, 1)

        เมื่อกำหนดให้แกน X แสดงจำนวนเสื้อที่ตัวขายได้เป็นตัว

        และ แกน Y แสดงจำนวนเสื้อที่แล้วขายได้เป็นตัว

กราฟแสดงความสัมพันธ์ระหว่างจำนวนเสื้อที่เป็นไปได้ซึ่งตั้วและแต้วขายได้เป็นดังนี้

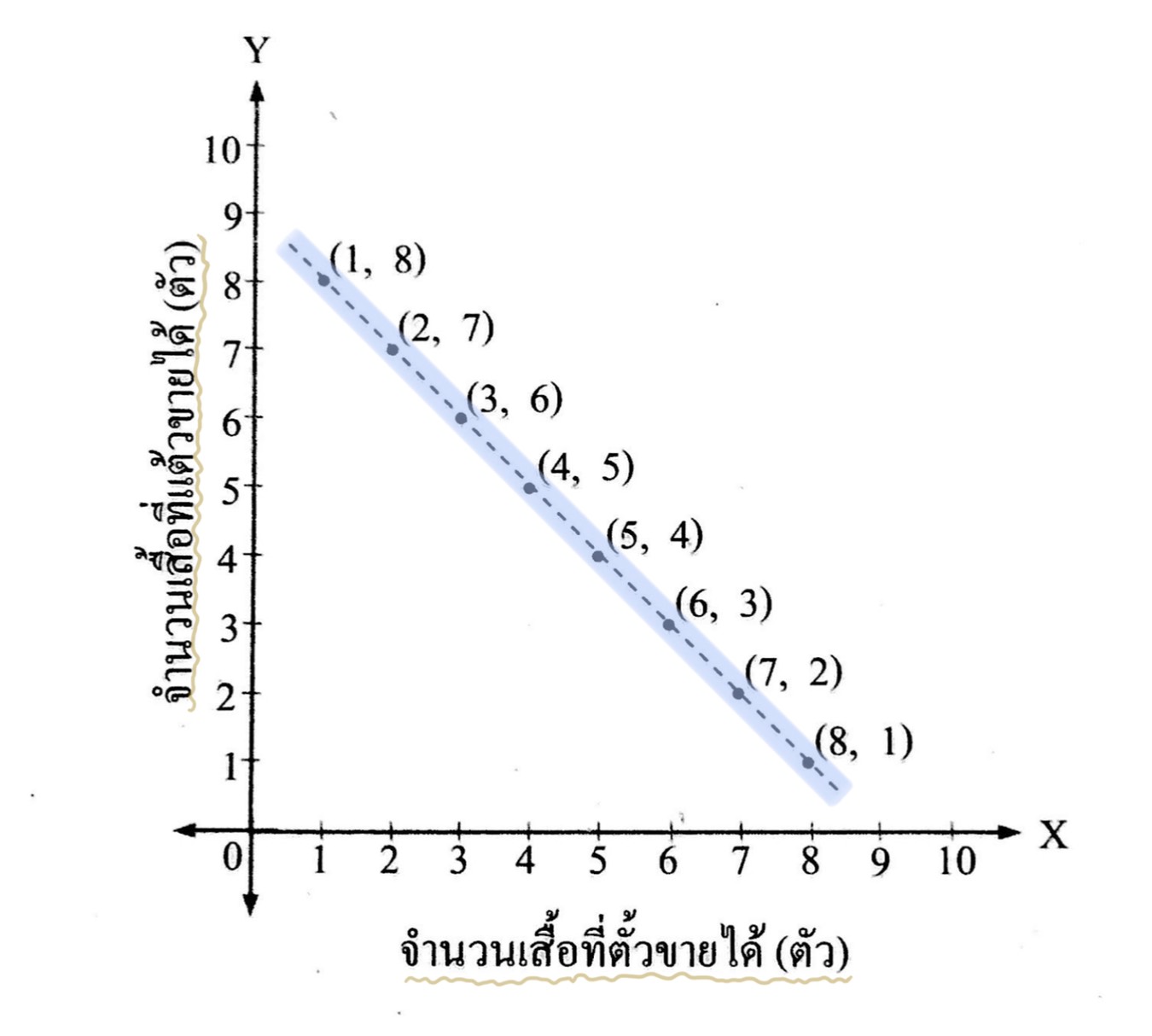
จากกราฟจะเห็นว่าทุกจุดของคู่อันดับที่เป็นไปตามเงื่อนไขในโจทย์ข้างต้น จะอยู่ในแนวเดียวกันกับเส้นประดังรูป นั่นคือ จุดทุกจุดของคู่อันดับที่เป็นไปตามเงื่อนไขที่กำหนดจะเรียงอยู่ในแนวเส้นตรงเดียวกัน

กราฟแสดงความสัมพันธ์ของอุณหภูมิ

ตัวอย่าง การบอกอุณหภูมิในประเทศไทยและหลายประเทศ นิยมบอกโดยใช้หน่วยเป็นองศาเซลเซียส (°C) แต่ก็มีบางประเทศ เช่น สหรัฐอเมริกาบอกอุณหภูมิโดยใช้หน่วยเป็นองศาฟาเรนไฮต์ (°F) ความสัมพันธ์ของอุณหภูมิทั้งสองหน่วย แสดงได้ด้วยสมการ F =(9/5)c+32

        มื่อ C แทนอุณหภูมิในหน่วยองศาเซลเซียส

     และ F แทนอุณหภูมิในหน่วยองศาฟาเรนไฮต์

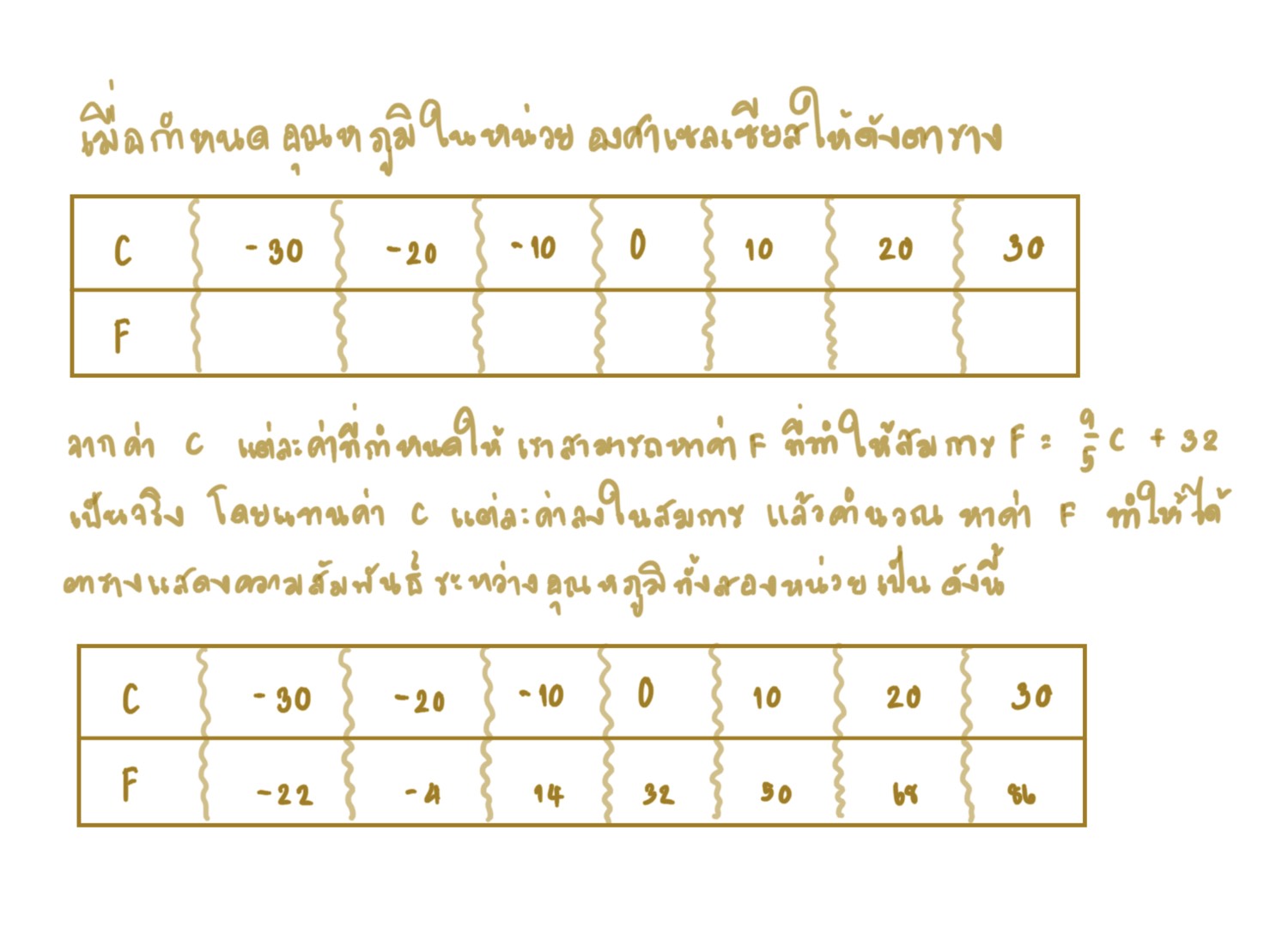
จากตารางเขียนคู่อันดับแสดงความสัมพันธ์ระหว่างอุณหภูมิในหน่วยองศาเซลเซียส กับอุณหภูมิในหน่วยองศาฟาเรนไฮต์ ได้ดังนี้ (-30, -22), (-20, 4), (-10, 14), (0, 32), (10, 50), (20, 68), (30, 86)

        เมื่อกำหนดให้แกน X แสดงอุณหภูมิในหน่วยองศาเซลเซียส

        แกน Y แสดงอุณหภูมิในหน่วยองศาฟาเรนไฮต์

จากข้อมูลในตารางเขียนกราฟแสดงความสัมพันธ์ระหว่างอุณหภูมิในหน่วยองศาเซลเซียสกับอุณหภูมิในหน่วยองศาฟาเรนไฮต์ ได้ดังนี้

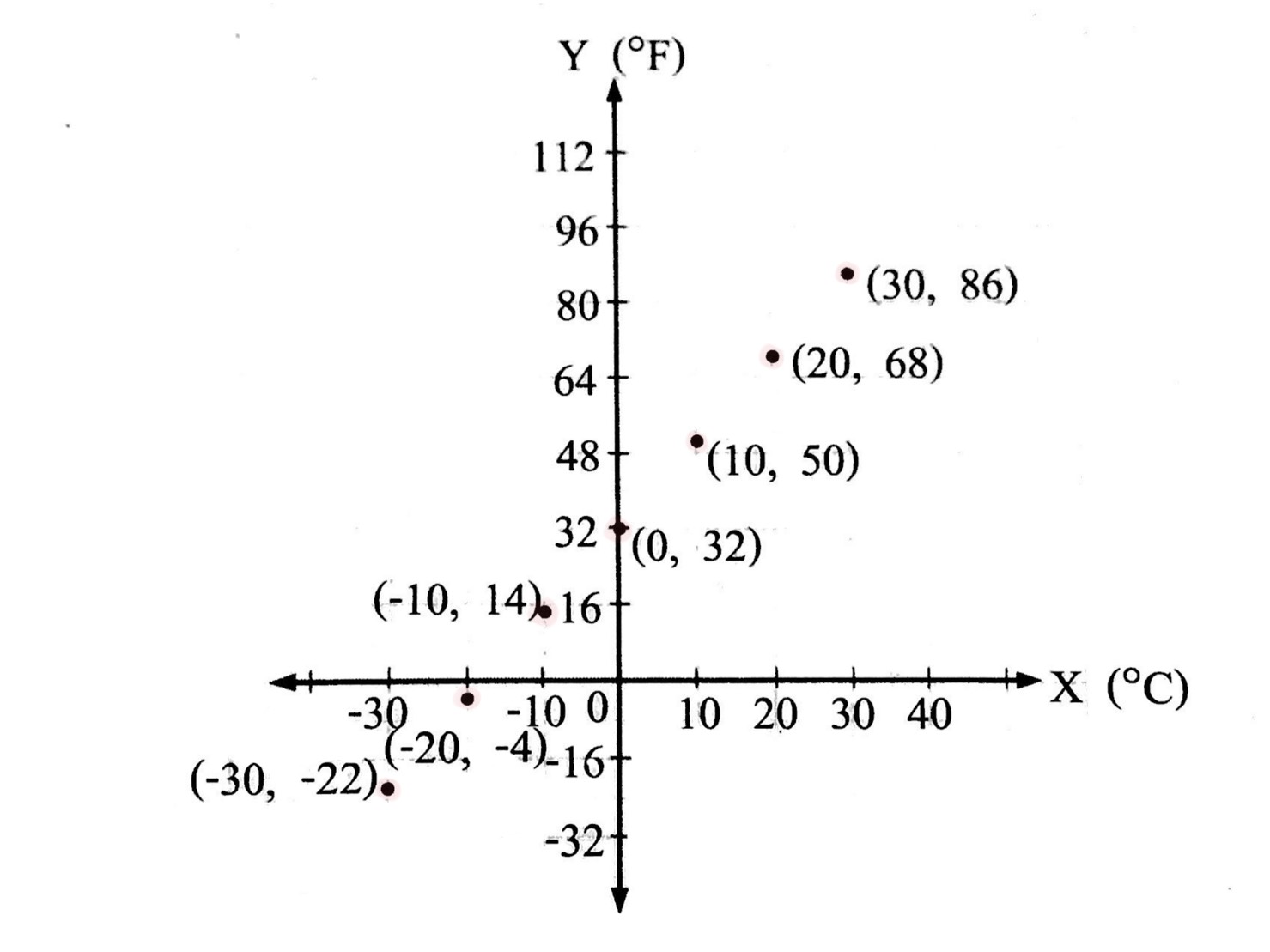
จากกราฟจะเห็นว่า จุดแต่ละจุดในกราฟซึ่งแสดงความสัมพันธ์ระหว่างอุณหภูมิในหน่วยองศาเซลเซียสกับอุณหภูมิในหน่วยองศาฟาเรนไฮต์อยู่ในแนวเส้นตรงเดียวกัน

เนื่องจากเราสามารถหาอุณหภูมิในหน่วยองศาฟาเรนไฮต์ได้เสมอ ไม่ว่าอุณหภูมิในหน่วยองศาเซลเซียสจะเป็นเท่าใด ดังนั้นจึงเขียนกราฟแสดงความสัมพันธ์ระหว่างอุณหภูมิในหน่วยองศาเซลเซียสกับอุณหภูมิในหน่วยองศาฟาเรนไฮต์ได้ในลักษณะที่ต่อเนื่องกันเป็นเส้นตรง ดังรูป

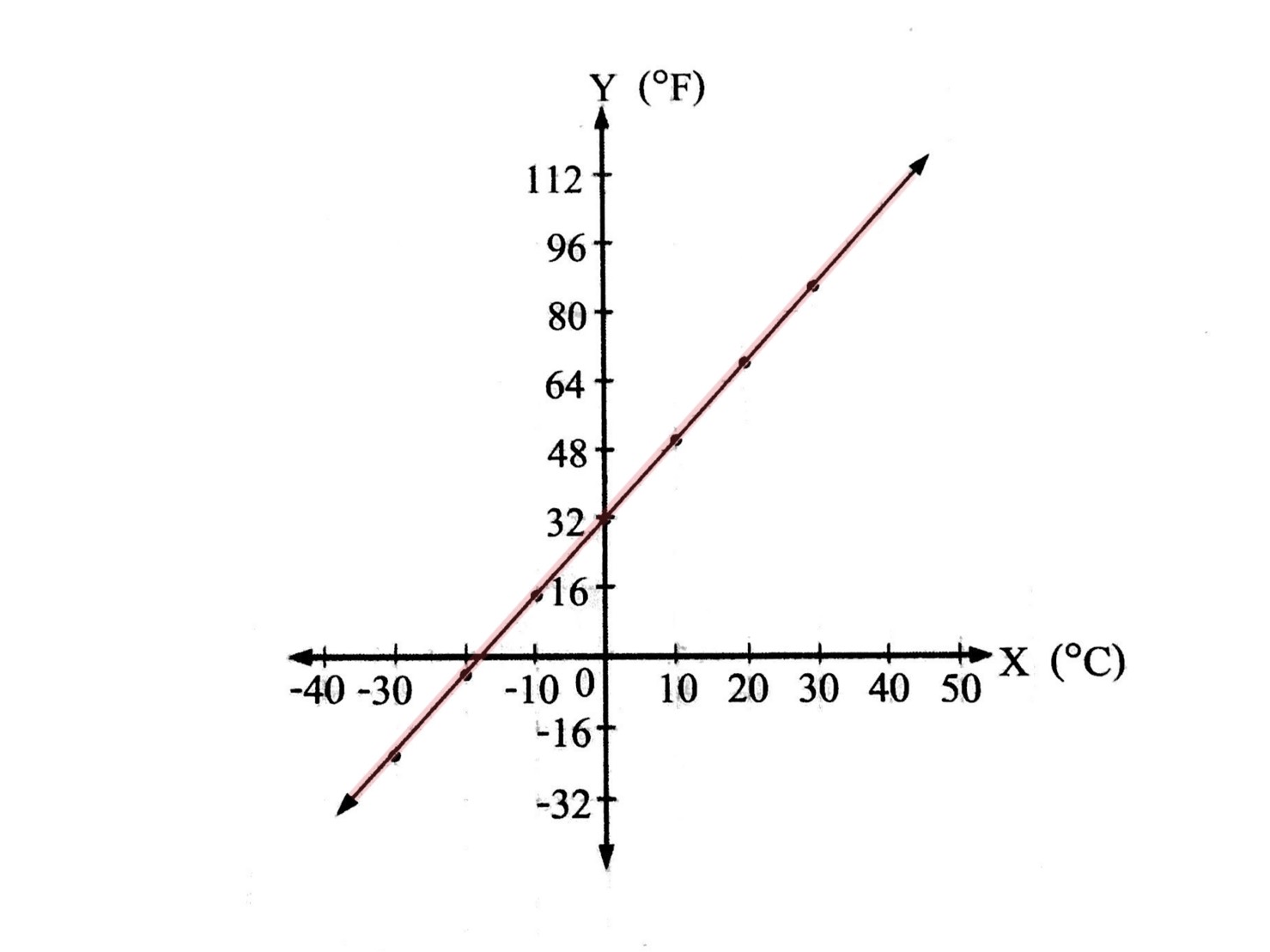
จากกราฟเราสามารถหาค่าประมาณของอุณหภูมิในหน่วยองศาฟาเรนไฮต์ เมื่อทราบอุณหภูมิในหน่วยองศาเซลเซียส หรือค่าประมาณของอุณหภูมิในหน่วยองศาเซลเซียส เมื่อทราบอุณหภูมิในหน่วยองศาฟาเรนไฮต์เช่น ที่อุณหภูมิ 5 ° C เป็นอุณหภูมิประมาณ 40 ° F หรือที่อุณหภูมิ 8 ° F เป็นอุณหภูมิประมาณ 13 ° C ค่าประมาณเหล่านี้ สามารถอ่านได้จากกราฟโดยตรงซึ่งทำได้ง่ายและรวดเร็วกว่าการคำนวณจากสูตร F =(9/5)c +32

สถานการณ์ข้างต้นเป็นตัวอย่างของความสัมพันธ์ของปริมาณสองชุดที่มีกราฟอยู่ในแนวเส้นตรงเดียวกัน เราเรียกความสัมพันธ์ลักษณะเช่นนี้ว่าความสัมพันธ์เชิงเส้น ในการเขียนกราฟของความสัมพันธ์เชิงเส้นกรณีที่กราฟมีลักษณะเป็นจุด เพื่อดูแนวโน้มของความสัมพันธ์เรานิยมเขียนต่อจุดเหล่านั้นให้เป็นส่วนหนึ่งของเส้นตรง

คลิปวิดีโอตัวอย่างเรื่องกราฟแสดงความสัมพันธ์ปริมาณเชิงเส้น