กราฟของสมการเชิงเส้นสองตัวแปร คือกราฟแสดงความสัมพันธ์ระหว่างปริมาณสองชุดที่มีความสัมพันธ์เชิงเส้นสองตัวแปรหรือกราฟเส้นตรง ซึ่งจะพบเห็นในชีวิตประจำวันทั้งในด้านวิทยาศาสตร์และสังคมศาสตร์
ความหมายของกราฟสมการเชิงเส้นสองตัวแปร
ความสัมพันธ์ระหว่างปริมาณสองชุดที่มีกราฟอยู่ในแนวเส้นตรงเดียวกันเป็นความสัมพันธ์เชิงเส้น พิจารณาความสัมพันธ์ต่อไปนี้
“สามเท่าของจำนวนเต็มจำนวนหนึ่งมากกว่าจำนวนเต็มอีกจำนวนหนึ่งอยู่ 10″
ถ้าให้ x แทนจำนวนเต็มจำนวนแรก
y แทนจำนวนเต็มจำนวนที่สอง
เขียนข้อความข้างต้นเป็นสมการได้เป็น 3x – y = 10
เมื่อกำหนดค่า x และหาค่า y ที่เป็นไปได้ตามเงื่อนไขของข้อความข้างต้น จะได้ ดังตารางต่อไปนี้
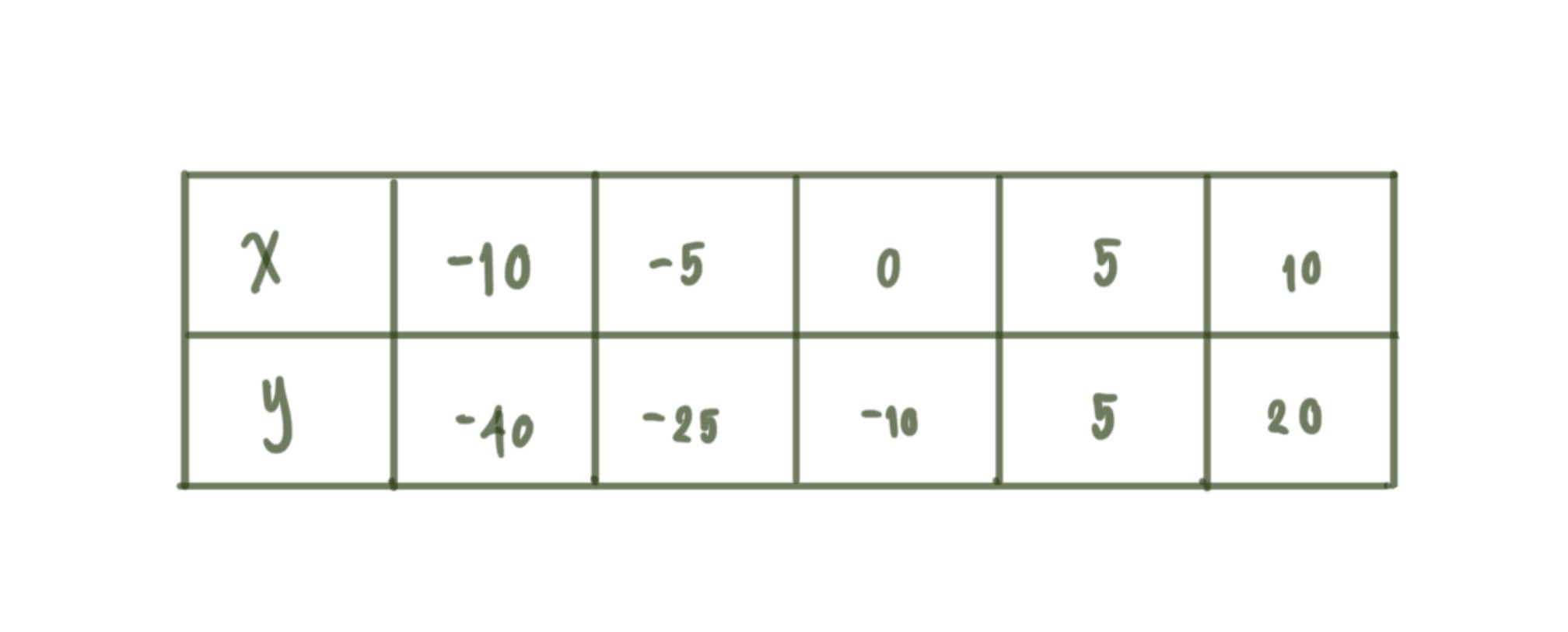จากตาราง คู่อันดับที่แสดงความสัมพันธ์ระหว่างจำนวนเต็มจำนวนแรกและจำนวนเต็มจำนวนที่สอง คือ (-10, -40), (-5, -25), (0, -10), (5, 5) และ (10, 20) นำคู่อันดับที่ได้มาเขียนกราฟได้ดังนี้
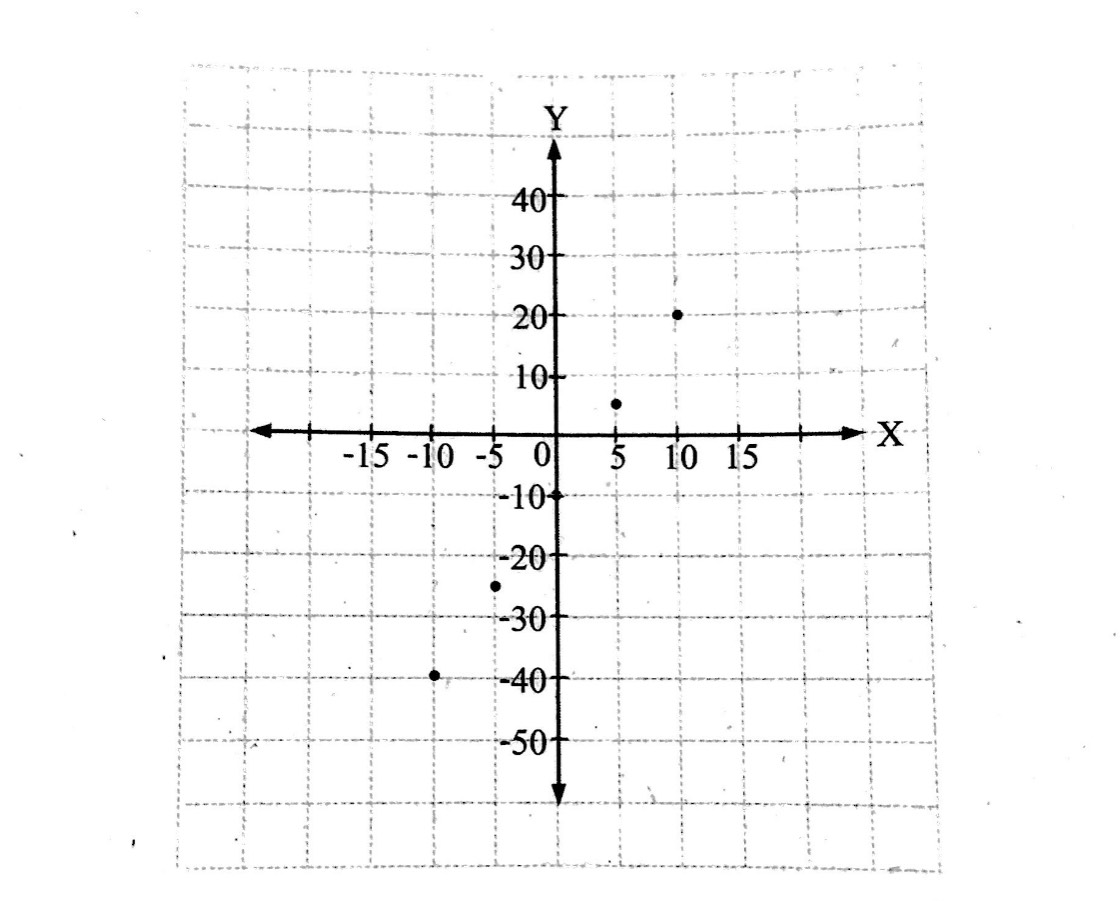
จากตัวอย่างข้างต้น จะเห็นว่า กราฟที่ได้เป็นจุดที่เรียงอยู่ในแนวเส้นตรงเดียวกันความสัมพันธ์ของจำนวนเต็มทั้งสองจึงเป็นความสัมพันธ์เชิงเส้น
สมการของความสัมพันธ์เชิงเส้นที่แสดงความเกี่ยวข้องระหว่างปริมาณสองชุดจะเรียกว่า “สมการเชิงเส้นสองตัวแปร”
ลักษณะสำคัญของสมการเชิงเส้นสองตัวแปร AX + By + C = 0 คือ มีตัวแปรสองตัวและต้องไม่มีการคูณกันของตัวแปร เลขชี้กำลังของตัวแปรแต่ละตัวต้องเป็นหนึ่ง สัมประสิทธิ์ตัวใดตัวหนึ่งเป็นศูนย์ได้ แต่สัมประสิทธิ์ของตัวแปรทั้งสองจะเป็นศูนย์พร้อมกันไม่ได้
กรณีที่กำหนดสมการเชิงเส้นสองตัวแปรในรูป Ar + By + C = 0 ถ้าไม่ระบุเงื่อนไขของ x และ y ให้ถือว่า x และ y แทนจำนวนจริงใด ๆ และกราฟของสมการเชิงเส้นสองตัวแปรนี้จะเป็นเส้นตรงที่เรียกว่า “กราฟเส้นตรง”
แก้สมาการของกราฟเชิงเส้นสองตัวแปร
เมื่อกำหนดสมการเชิงเส้นสองตัวแปรให้ เราสามารถหาคู่อันดับ (x,y) ที่เมื่อแทนค่า x และค่า y ในสมการแล้วทำให้สมการเป็นจริง โดยการกำหนดค่า x แล้วหาค่า y จากสมการ ดังตัวอย่างเช่น
เมื่อนำคู่อันดับที่สอดคล้องกับสมการ 5x+3y-10=0 เช่น (-1,5) ,(0,10/3) และ (2,0) มาเขียนกราฟ จะได้กราฟเป็นจุดที่อยู่ในแนวเส้นตรงเดียวกัน ดังนี้
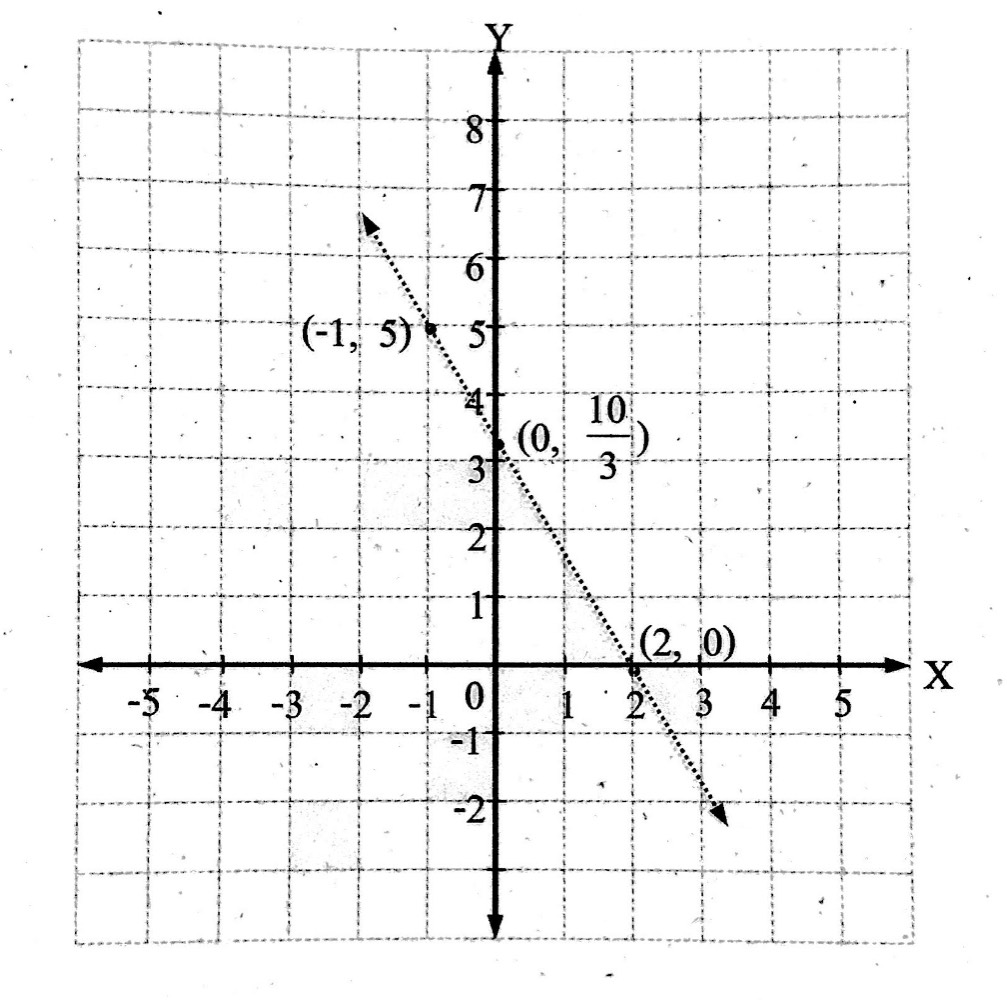
ในกรณีที่ไม่ระบุเงื่อนไขของ x และ y ในสมการเช่น 5x+3y-10=0 ให้ถือว่า x และ y แทนจำนวนจริงใดๆ นั่นหมายความว่า ยังมีคู่อันดับ (x,y) เหล่านั้นก็จะอยู่บนเส้นตรงที่เป็นกราฟของสมการนี้ด้วย
คลิปวิดีโอตัวอย่างเรื่องกราฟของสมการเชิงเส้นสองตัวแปร
