แบบฝึกหัดการให้เหตุผล

แบบฝึกหัดการให้เหตุผล ประกอบไปด้วยการให้เหตุผลแบบอุปนัยและการให้เหตุผลแบบนิรนัย ซึ่งแบบฝึกหัดนี้จะช่วยให้น้องๆได้ฝึกฝนการทำโจทย์จนน้องๆเชี่ยวชาญและส่งผลให้น้องๆทำข้อสอบได้แบบไม่ผิดพลาด ถ้าเรารู้เฉยๆเราอาจจะทำข้อสอบได้แต่การที่เราฝึกทำโจทย์ด้วยจะทำให้เราทำข้อสอบได้แน่นอนค่ะ

แบบฝึกหัดเพิ่มเติมและข้อสอบ O-Net

ตัวอย่างต่อไปนี้เป็นข้อสอบ O-Net ของปีก่อนๆ

1.) พิจารณาการอ้างเหตุผลต่อไปนี้

ก. เหตุ 1. ถ้าฝนไม่ตกแล้วเดชาไปโรงเรียน

  2. ฝนตก

     ผล    เดชาไม่ไปโรงเรียน

ข. เหตุ 1. รัตนาขยันเรียน หรือรัตนาสอบชิงทุนรัฐบาลได้

  2. รัตนาไม่ขยันเรียน

      ผล  รัตนาสอบชิงทุนรัฐบาลได้

พิจารณาว่า ก และ ข สมเหตุสมผลหรือไม่

พิจารณา ก เหตุที่ 1 ถ้าฝนไม่ตกแล้วเดชาไปโรงเรียน เขียนเป็นแผนภาพจะได้ ดังนี้

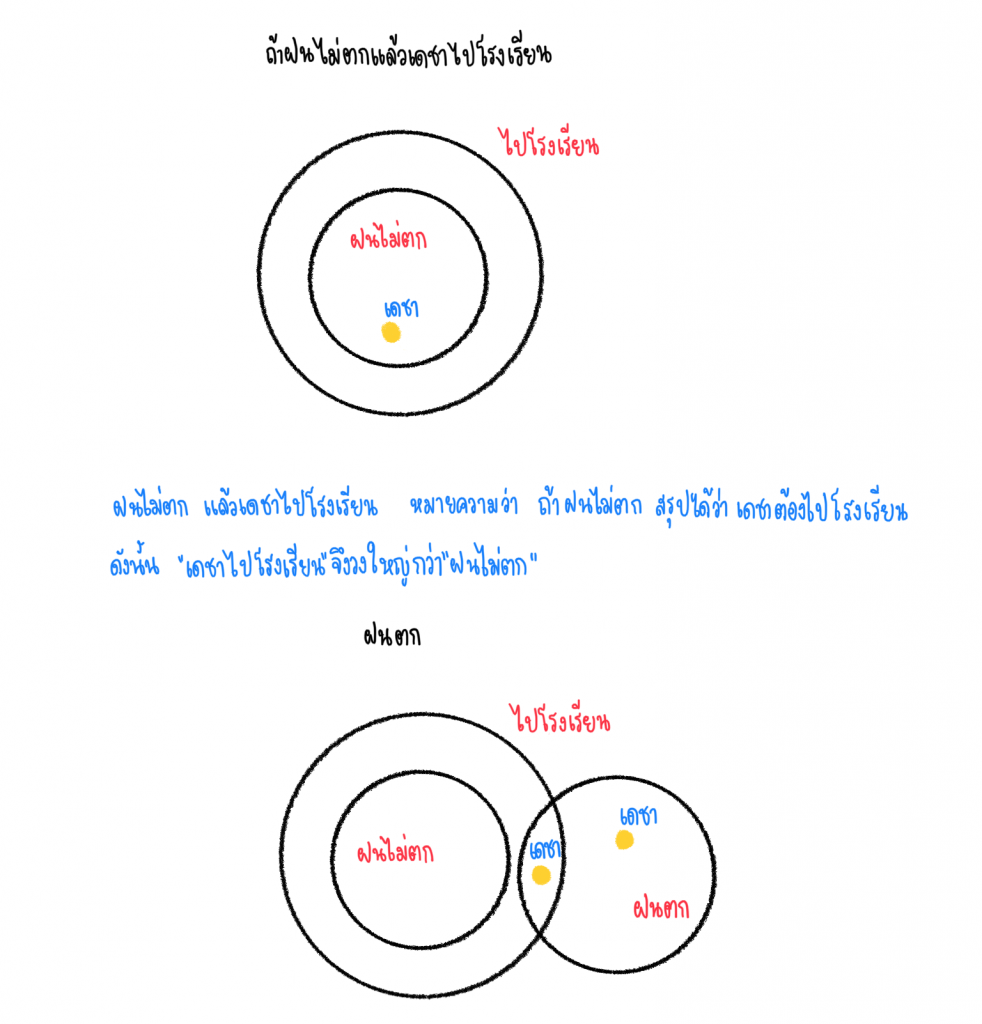
จะเห็นว่า ถ้าฝนตก สามารถเป็นไปได้ 2 กรณี คือ 1. เดชาไปโรงเรียน และ 2. เดชาไม่ไปโรงเรียน

ดังนั้น ก ไม่สมเหตุสมผล

พิจารณา ข เหตุที่ 1 รัตนาขยันเรียน หรือรัตนาสอบชิงทุนรัฐบาลได้

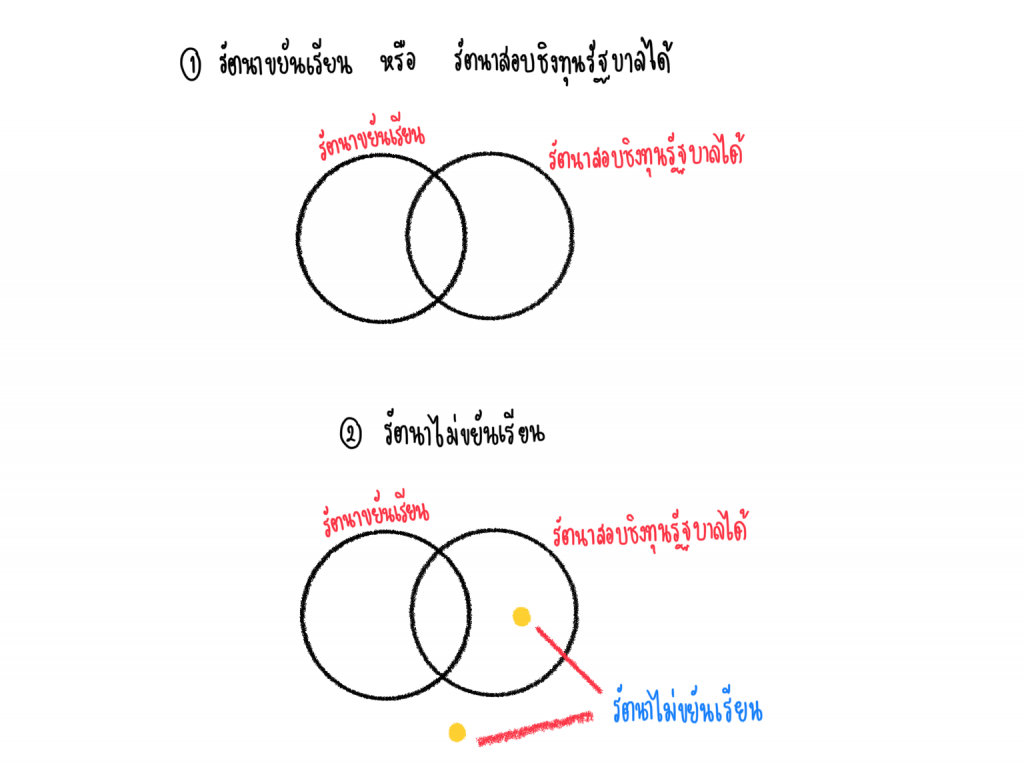
จะเห็นว่า ถ้ารัตนาไม่ขยันเรียนแล้ว จะเป็นไปได้ 2 กรณี คือ รัตนาสอบชิงทุนได้ กับรัตนาสอบชิงทุนไม่ได้

ดังนั้น ข ไม่สมเหตุสมผล

2.) พิจารณาข้อความต่อไปนี้

เหตุ 1. นกเป็นสิ่งมีชีวิต

2. ปลาเป็นสิ่งมีชีวิต

3. คนเป็นสิ่งมีชีวิต

ผล  สัตว์เป็นสิ่งมีชีวิต

ข้อความดังกล่าวเป็นการให้เหตุผลแบบใด

ตอบ  การให้เหตุผลแบบอุปนัย เพราะเป็นการสรุปผลจากประสบการณ์หรือสิ่งที่สังเกตได้

3.)   จงพิจารณาเหตุต่อไปนี้

1) ทุกคนที่ชอบกินผลไม้จะชอบกินผัก
2) ทุกคนที่ชอบรสหวานจะชอบกินผลไม้
3) ขาวไม่ชอบกินผัก
4) ดาชอบกินผลไม้

ผลสรุปในข้อใดต่อไปนี้ทำให้การให้เหตุผลสมเหตุสมผล

1. ขาวไม่ชอบรสหวาน

2. ขาวชอบกินผลไม้

3. ดาชอบรสหวาน

4. ดาไม่ชอบรสหวาน

5. ดาไม่ชอบกินผัก

เราจะใช้แผนภาพเวนน์-ออยเลอร์ ในการพิจารณาการให้เหตุผล

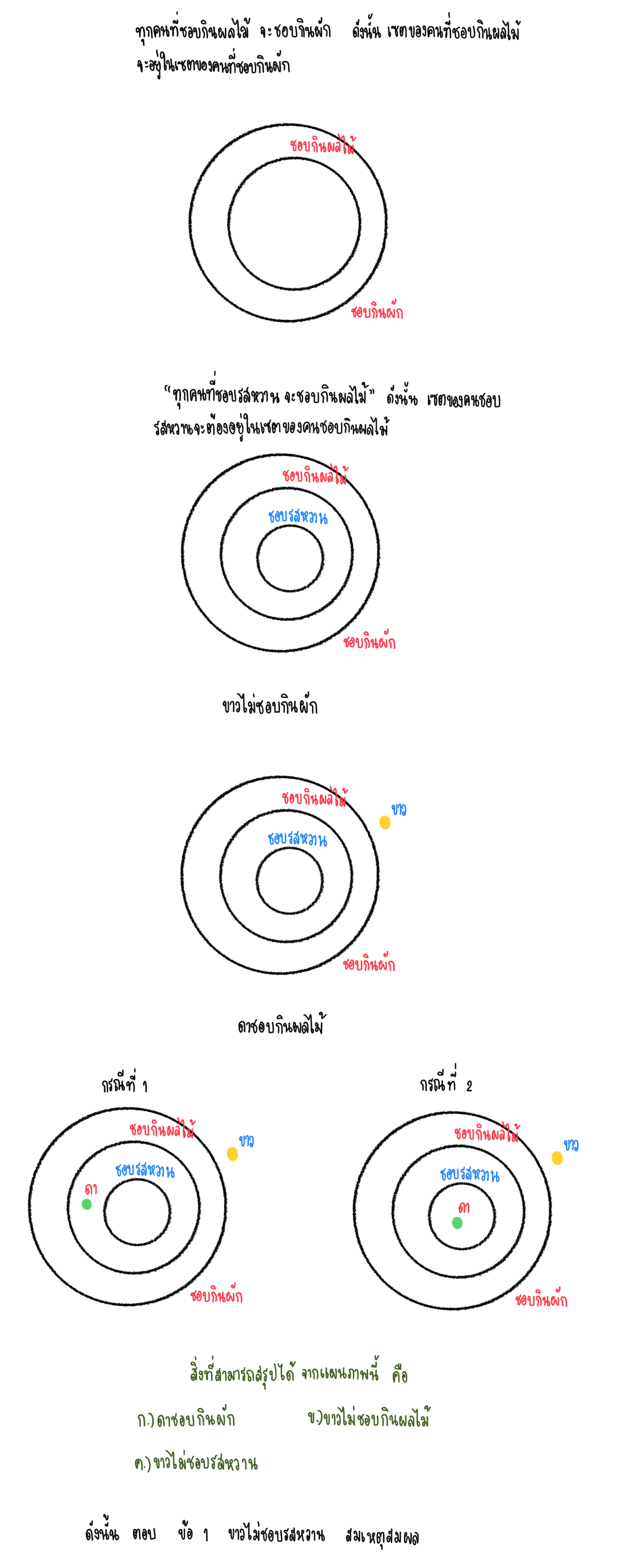
พิจารณา ข้อ 2 ขาวชอบผลไม้ ข้อนี้เห็นได้ชัดเลยว่าไม่สมเหตุสมผล เนื่องจากขาวอยู่นอกวงกลมของชอบกินผัก ดังนั้นขาวไม่มีทางที่จะชอบกินผลไม้แน่นอน

พิจารณา ข้อ 3 ดาชอบรสหวาน ข้อนี้ไม่สมเหตุสมผล เพราะ จากเหตุที่บอกว่า ดาชอบกินผลไม้ ทำให้เกิดกรณีได้ 2 กรณี คือ ดาชอบรสหวานกับดาไม่ชอบรสหวาน

พิจารณาข้อ 4 ดาไม่ชอบรสหวาน ข้อนี้ก็ไม่สามารถสรุปได้เหมือนกับข้อ 3

พิจารณาข้อ 5 ดาไม่ชอบกินผัก ข้อนี้เห็นได้ชัดเลยว่าไม่สมเหตุสมผล เพราะดาชอบกินผลไม้ แล้วคนที่ชอบกินผลไม้ทุกคนชอบกินผัก ดังนั้นเป็นไปไม่ได้ที่ดาจะไม่ชอบกินผัก

4.)

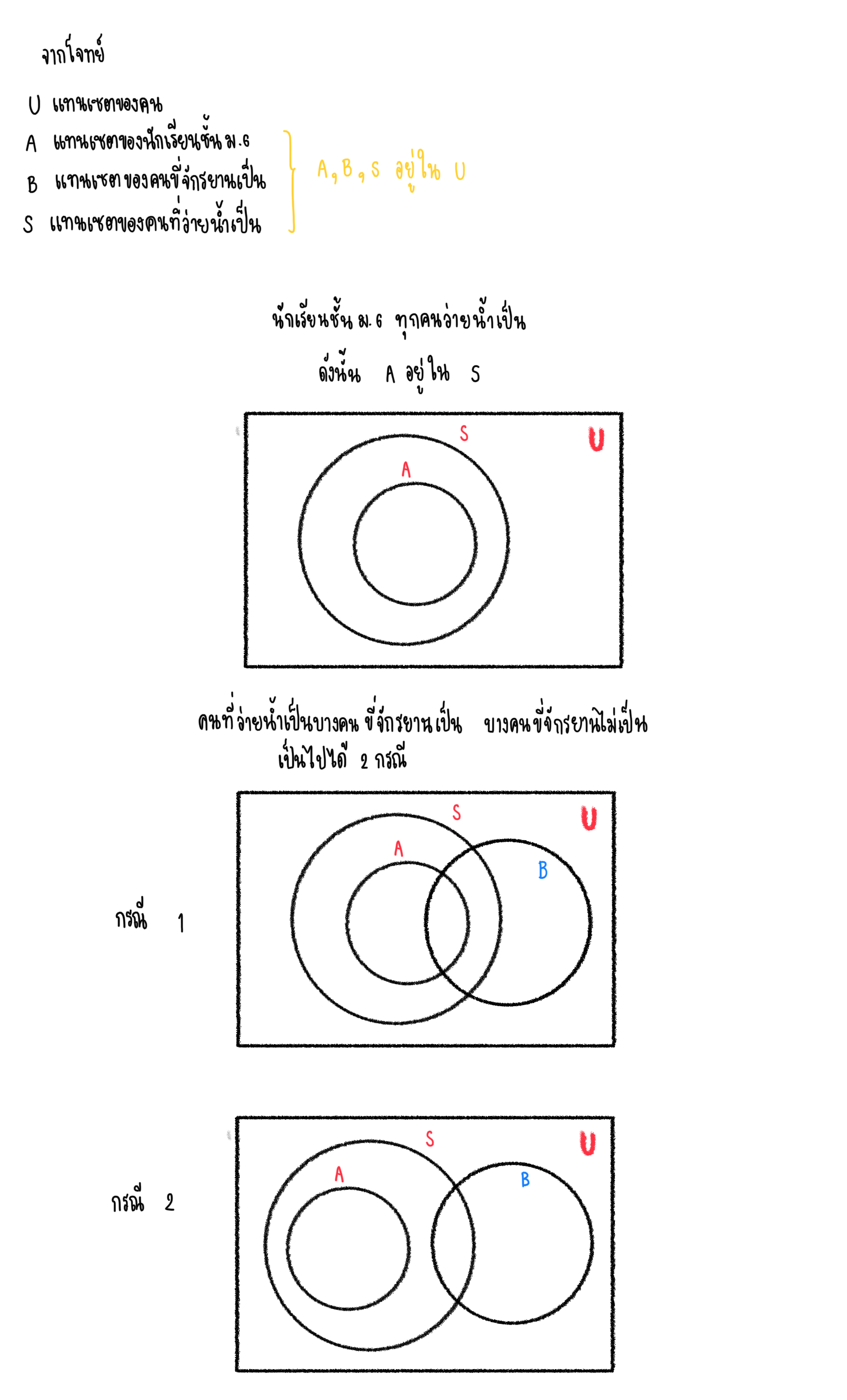
เหตุ 1. นักเรียนชั้น ม.6 ทุกคนว่ายน้ำเป็น

2. คนที่ว่ายน้ำเป็น บางคนขี่จักรยานเป็น บางคนขี่จักรยานไม่เป็น

ถ้าให้ U แทนเซตของคน

A แทนเซตของนักเรียนชั้น ม.6

B แทนเซตของคนที่ขี่จักรยานเป็น

S แทนเซตของคนที่ว่ายน้ำเป็น

ข้อความที่กำหนดให้สอดคล้องกับแผนภาพเวนน์-ออยเลอร์ในข้อใดต่อไปนี้

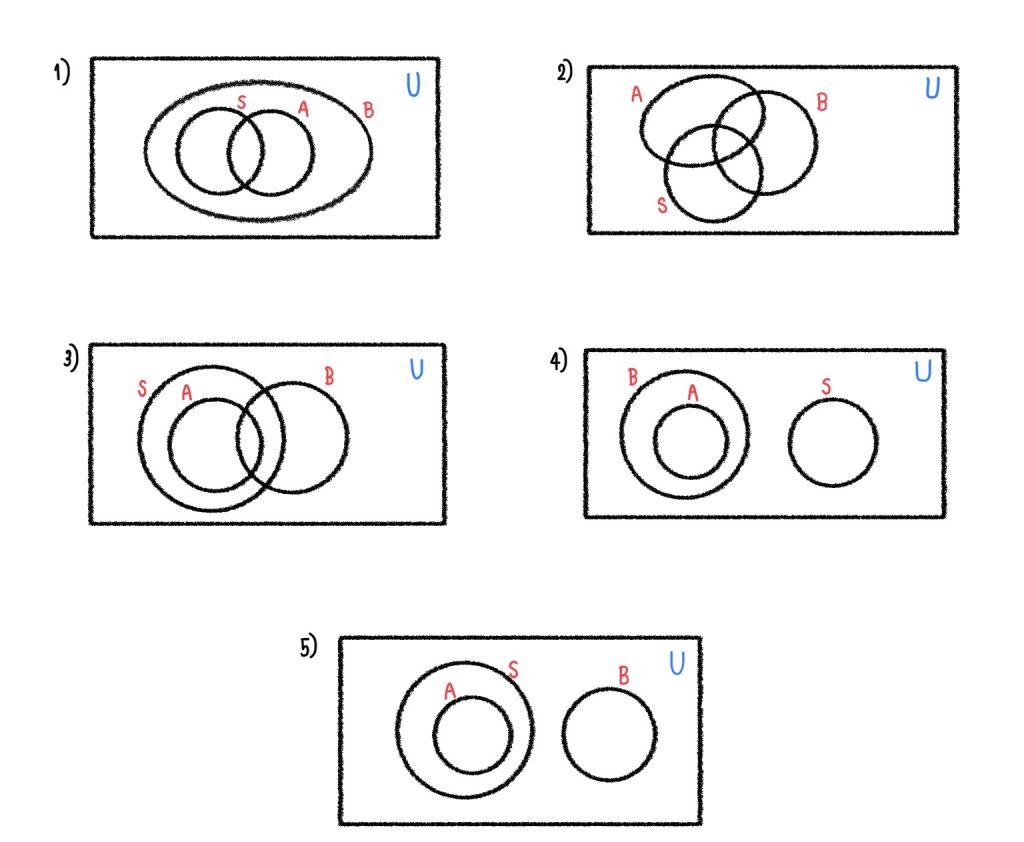
พิจารณาข้อความที่โจทย์กำหนดให้เป็นแผนภาพเวนน์-ออยเลอร์ ได้ดังนี้

5.) พิจารณาประโยคต่อไปนี้ว่าเป็นการให้เหตุผลแบบอุปนัยหรือนิรนัย

5.1) เกรดเทอมนี้ไม่ดีหรอก เพราะเทอมที่ผ่านมาเกรดก็ไม่ดี

ตอบ เป็นการให้เหตุผลแบบอุปนัย เพราะใช้ประสบการณ์จากเทอมก่อนๆมาสรุป

5.2) เทอมนี้ต้องได้เกรดดีแน่ๆ เพราะคนขยันเรียนจะได้เกรดดี แล้วเทอมนี้ฉันก็ขยันเรียน

ตอบ เป็นการให้เหตุผลแบบนิรนัย เพราะเรากำหนดไว้แล้วว่า คนขยันเรียนจะได้เกรดดี ดังนั้นถ้าเราขยันเรียนต้องได้เกรดดี

5.3) ที่ผ่านมาฉันสังเกตเห็นว่าทุกครั้งที่อากาศร้อนอบอ้าว ฝนจะตกตลอดเลย วันนี้ฝนต้องตกแน่ๆ เพราะอากาศร้อนอบอ้าว

ตอบ เป็นการให้เหตุผลแบบนิรนัย เพราะเหมือนเรากำหนดไว้ว่า ทุกครั้งที่อากาศร้อนอบอ้าวฝนจะตก

5.4) ที่ผ่านมาฉันโชคไม่ค่อยดีเลย วันนี้ฉันต้องโชคไม่ดีอีกแน่ๆ

ตอบ เป็นการให้เหตุผลแบบอุปนัย เพราะใช้ประสบการณ์จากครั้งก่อนๆที่โชคไม่ดี มาสรุปว่าวันนี้ก็ต้องโชคไม่ดีอีก

6.) พิจารณาข้อความที่กำหนดให้ แล้วใช้การให้เหตุผลแบบอุปนัย หาคำตอบ

6.1) 

(1×9) + 2 = 11

(12×9) + 3 = 111

(123×9) + 4 = 1111

(___×__) + __ = _____

ตอบ (1234 × 9) + 5 = 11111

6.2)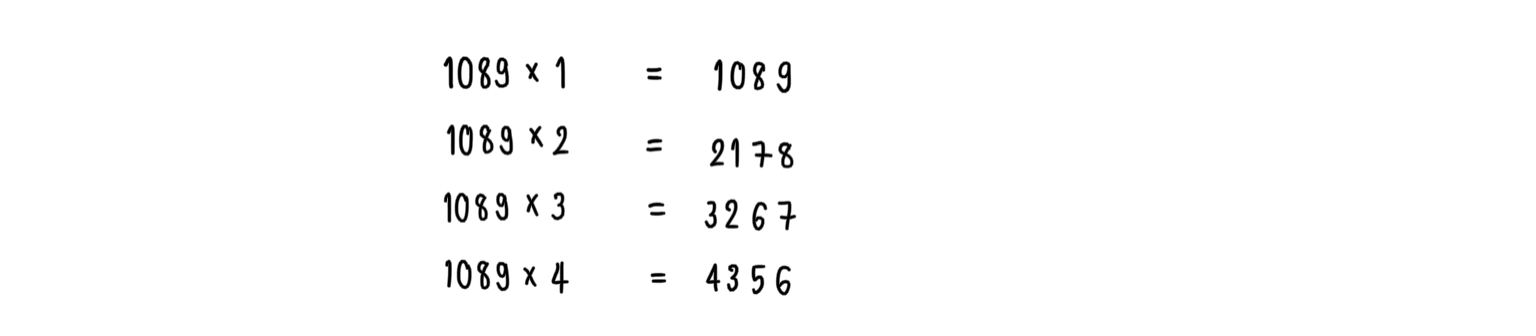

อีกสามพจน์ต่อไปคือ?

ตอบ 1089 × 5 = 5445 , 1089 × 6 = 6534 , 1089 × 7 = 7623

เนื้อหาที่ควรรู้ในการทำโจทย์การให้เหตุผล และวีดิโอเพิ่มเติม

หากน้องๆคนไหนยังรู้สึกว่าตัวเองไม่แม่นเรื่องการให้เหตุผลสามารถเข้าไปดูบทความการให้เหตุผลแบบนิรนัยและอุปนัยพร้อมดูตัวอย่างเพิ่มเติมได้ที่

>> การให้เหตุผลแบบอุปนัย

>> การให้เหตุผลแบบนิรนัย

>> การตรวจสอบการให้เหตุผล

หรือสามารถดูวีดิโอ เพิ่มเติมข้างล่างนี้ได้เลย