ข้อสอบO-Net
ข้อสอบO-Net ในบทความนี้จะคัดเฉพาะเรื่องจำนวนจริงมาให้น้องๆทุกคนได้ดูว่าที่ผ่านมาแต่ละปีข้อสอบเรื่องจำนวนจริงออกแนวไหนบ้าง โดยบทความนี้พี่ได้นำข้อสอบย้อนหลังของปี 49 ถึงปี 52 มาให้น้องๆได้ดูพร้อมเฉลยอย่างละเอียด เมื่อน้องๆได้ศึกษาโจทย์ทั้งหมดและลองฝึกทำด้วยตัวเองแล้ว น้องๆจะสามารถทำข้อสอบทั้งของในโรงเรียนและข้อสอบO-Net ได้แน่นอนค่ะ
ข้อสอบO-Net เรื่องจำนวนจริง ปี 49
1. มีค่าเท่ากับข้อในต่อไปนี้
- 60
-
-
- 200
คำตอบ 4

2. มีค่าเท่ากับข้อใดต่อไปนี้
คำตอบ 1

3. ค่าของ x ที่สอดคล้องกับสมการ เท่ากับข้อใดต่อไปนี้
- 2
- 3
- 4
- 5
คำตอบ 3

4. กำหนดให้ a, b เป็นจำนวนจริงใดๆ ข้อใดต่อไปนี้ถูกต้อง
- ถ้า a < b แล้ว จะได้
- ถ้า a < b < 0 แล้ว จะได้
- ถ้า
แล้ว จะได้ a < b
- ถ้า
แล้ว จะได้ a < b
คำตอบ 2
ถ้าเจอโจทย์แบบนี้ให้ลองแทนตัวเลขที่ทำให้แต่ละผิด
พิจารณาข้อ 1 สมมติให้ a = -3 และ b = 1 จะเห็นว่า -3 < 1 นั่นคือ a < b
เมื่อเรายกกำลังสองทั้ง a และ b จะได้ว่า a² = 9 และ b² = 1 จะเห็นว่า 1 < 9 นั่นคือ b² < a²
ดังนั้น ข้อ 1 ผิด
พิจารณาข้อ 3 กรณีที่ a = -1 b = -2 ทำให้ข้อความข้างต้นเป็นเท็จ เพราะเมื่อยกกำลังสอง a² < b² จริง แต่ a < b ไม่จริง
ดังนั้น ข้อ 3 ผิด
พิจารณา ข้อ 4 สมมติให้ a = 1 b = -2 จะเห็นว่า จริง แต่ a < b นั้นไม่จริง
ดังนั้น ข้อ 4 ผิด
5.) อสมการในข้อใดต่อไปนี้เป็นจริง
คำตอบ 3
ทำให้เลขยกกำลังเท่ากัน
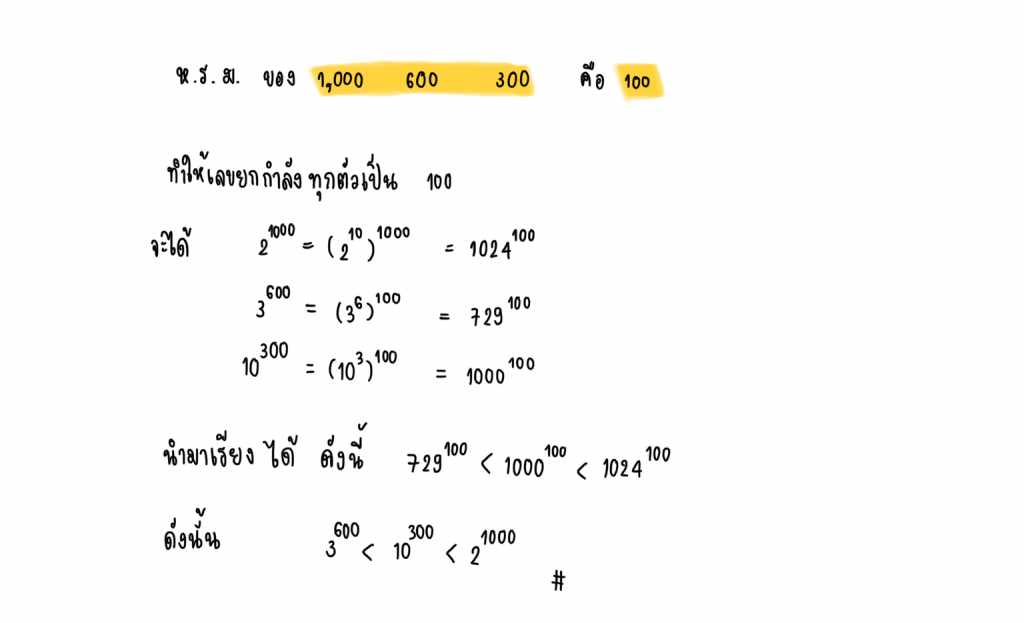
6.) ถ้า และ
แล้ว a + b มีค่าเท่ากับเท่าใด
ตอบ 0.75

ข้อสอบO-Net เรื่องจำนวนจริง ปี 49
1.) มีค่าเท่ากับข้อใดต่อไปนี้
คำตอบ 4

2.) มีค่าเท่ากับข้อใดต่อไปนี้
-
-
- 2
- 3
คำตอบ 3

3.) มีค่าเท่ากับข้อใดต่อไปนี้
- -32
- -24
-
-
คำตอบ 1

4.) ถ้า x ≤ 5 แล้ว ข้อใดต่อไปนี้ถูกต้อง
คำตอบ 1

5.) ถ้า แล้ว x มีค่าาเท่ากับข้อใดต่อไปนี้
คำตอบ 1

6.) ถ้า เป็นรากของสมการ
แล้ว รากอีกรากหนึ่งของสมการนี้ มีค่าเท่ากับข้อใดต่อไปนี้
- -5
-
-
- 5
คำตอบ 3

7.) เซตคำตอบของอสมการ คือเซตในข้อใดต่อไปนี้
คำตอบ 4

ข้อสอบ O-Net เรื่องจำนวนจริง ปี 50
1.) มีค่าเท่ากับข้อใดต่อไปนี้
คำตอบ 1

2.) ถ้า แล้ว x มีค่าเท่ากับข้อใดต่อไปนี้
คำตอบ 2

3.) เซตคำตอบของอสมการ คือเซตในข้อใดต่อไปนี้
คำตอบ 3

4.) สมการในข้อใดต่อไปนี้ มีคำตอบที่เป็นจำนวนจริงมากกว่า 2 คำตอบ
คำตอบ 4

5.) ผลบวกของคำตอบทุกคำตอบของสมการ เท่ากับข้อใดต่อไปนี้
- 0
-
-
-
คำตอบ 1
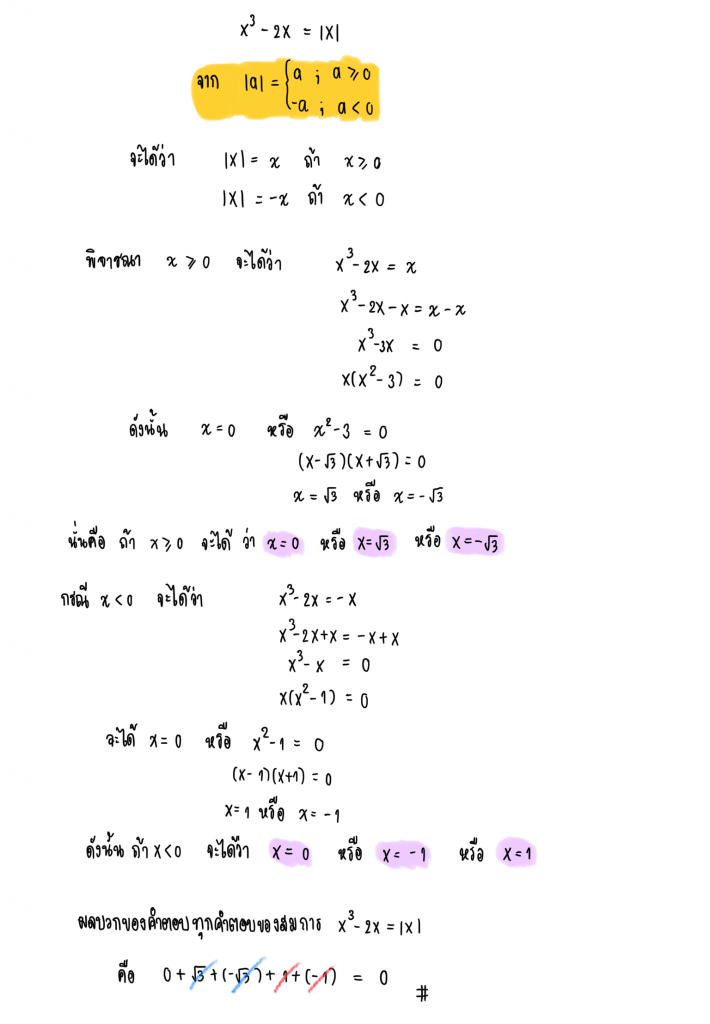
ข้อสอบ O-Net เรื่องจำนวนจริง ปี 51
1.) ค่าของ เท่ากับข้อใดต่อไปนี้
- -1
- 1
- 3
- 5
คำตอบ 3

2.) กำหนดให้ค่าประมาณที่ถูกต้องถึงทศนิยมตำแหน่งที่ 3 ของ และ
คือ 1.732 และ 2.236 ตามลำดับ
พิจารณาข้อความต่อไปนี้
ก.
ข.
ข้อสรุปใดต่อไปนี้ถูกต้อง
- ถูกทั้ง 2 ข้อ
- ก ถูก ข ผิด
- ก ผิด ข ถูก
- ผิดทั้ง 2 ข้อ
คำตอบ 1

4.) พืจารณาข้อความต่อไปนี้
ก. สมบัติการมีอินเวอร์สการบวกของจำนวนจริงกล่าวว่า
สำหรับจำนวนจริง a จะมีจำนวนจริง b ที่ b + a = 0 = a + b
ข. สมบัติการมีอินเวอร์สการคูณของจำนวนจริง กล่าวว่า
สำหรับจำนวนจริง a จะมีจำนวนจริง b ที่ ba = 1 = ab
ข้อสรุปใดต่อไปนี้ถูกต้อง
- ถูกทั้ง 2 ข้อ
- ก ถูก ข ผิด
- ก ผิด ข ถูก
- ผิดทั้ง 2 ข้อ
คำตอบ 1
ก.จริง เพราะ ยกตัวอย่าง a = 1 ตัวที่บวกกับ 1 แล้วได้ 0 คือ -1 นั่นคือ -1 เป็นอินเวอร์การบวกของ 1
ข. จริง เพราะ สมมติให้ a = 2 ตัวที่คูณกับ 2 แล้วได้ 1 คือ นั่นคือ
เป็นอินเวอร์สการคูณของ 2
จึงสรุปได้ว่า ก และ ข ถูก
**คำว่า “มี” แปลว่าอาจจะมีแค่ตัวเดียวหรือหลายตัวก็ได้ ถ้าเรายกตัวอย่างมาได้สัก 1 ตัวอย่างที่เป็นจริงก็ถือว่า ข้อความนั้นเป็นจริง**
แต่ต้องระวัง ถ้าเจอคำว่า”ทุกๆ” หรือตำว่า “แต่ละตัว” การที่เราจะบอกว่าทุกตัวมันจริงคงไม่ไหวเพราะมันอาจจะมีจำนวนมาก ดังนั้นน้องๆควรยกตัวอย่างมาค้านว่าข้อความนั้นเป็นเท็จจะง่ายกว่า
5.) พิจารณาสมการ ข้อใดต่อไปนี้เป็นเท็จ
- คำตอบหนึ่งของสมการมีค่าระหว่าง 10 และ 15
- ผลบวกของคำตอบทั้งหมดของสมการมีค่าเท่ากับ 14
- สมการนี้มีคำตอบมากกว่า 2 คำตอบ
- ใบบรรดาคำตอบทั้งหมดของสมการ คำตอบที่มีค่าน้อยที่สุดมีค่าน้อยกว่า 3
คำตอบ 3

ข้อสอบ O-Net เรื่องจำนวนจริง ปี 52
1.) พิจารณาข้อความต่อไปนี้
ก. จำนวนที่เป็นทศนิยมไม่รู้จบบางจำนวนเป็นจำนวนอตรรกยะ
ข. จำนวนที่เป็นทศนิยมไม่รู้จบบางจำนวนเป็นจำนวนตรรกยะ
ข้อใดถูกต้อง
- ก และ ข
- ก เท่านั้น
- ข เท่านั้น
- ก และ ข ผิด
คำตอบ 2
ก. จากที่เรารู้อยู่แล้วว่าทศนิยมไม่รู้จบเป็นจำนวนอตรรกยะ ข้อความนี้จึงถูกต้อง
ข. ผิด เพราะจำนวนตรรกยะคือจำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มได้ แต่ทศนิยมไม่รู้จบไม่สามารถเขียนในรูปเศษส่วนของจำนวนเต็มได้ ดังนั้นจึงไม่มีจำนวนตรรกยะใดที่เป็นจำนวนที่เป็นทศนิยมไม่รู้จบ
2.) ผลเฉลยของสมการ อยู่ในช่วงใด
- (-10, -5)
- (-6, -4)
- (-4, 5)
- (-3, 6)
คำตอบ 4

3.) ถ้า เป็นผลเฉลยหนึ่งของสมการ
เมื่อ b เป็นจำนวนจริงแล้ว อีกผลเฉลยหนึ่งของสมการนี้มีค่าตรงกับข้อใด
- -2
-
-
- 2
คำตอบ 1

4.) ข้อใดมีค่าต่างจากข้ออื่น
คำตอบ 2

5.) เท่ากับข้อใด
- 0
- 180
- 192
- 200
คำตอบ 1

วิดีโอ ข้อสอบO-Net เรื่องจำนวนจริง



















