การอ้างเหตุผล คือการตรวจสอบว่าข้อความที่กำหนดให้ชุดหนึ่งจะสร้างข้อความใหม่อีกข้อความหนึ่ง อาจจะสมเหตุสมผลหรือไม่ก็ได้ ถ้าอ้างเหตุผลถูกต้อง ประกอบด้วย

• เหตุ คือสิ่งที่ถูกกำหนดให้ ประกอบด้วยประพจน์ย่อยๆ
• ผล คือ ผลสรุปจากเหตุ แทนด้วย Q

 

การพิจารณาการอ้างเหตุผล

• ถ้า ( )→Q เป็นสัจนิรันดร์ แล้ว การอ้างเหตุผล สมเหตุสมผล (valid)
• ถ้า () →Q ไม่เป็นสัจนิรันดร์ แล้ว การอ้างเหตุผล ไม่สมเหตุสมผล (invalid)

กฎที่ใช้ในการอ้างเหตุผล

1.) Modus Ponens

เหตุ  1.  p → q

2.  p

ผล        q

2.) Modus Tollens

เหตุ  1.  p →  q

2. ∼q

ผล       ∼p

3.) Law of Syllogism

เหตุ  1.  p   →   q

2.  q   →   r

ผล        p   →   r

4.) Disjunctive Syllogism

เหตุ   1.   ∼p   ∨   q

2.    p

ผล            q

5.) Law of simplification

เหตุ        p   ∧   q

ผล          p

6.) Law of addition

เหตุ   p

ผล    p   ∨   q

7.) Law of contraposition

เหตุ    p   →   q

ผล   ∼q   → ∼p

8.) Inference by cases

เหตุ  1.   p   →   r

2.   q   →   r

ผล    (p∨q)   →   r

**เทคนิคเหล่านี้อาจจะต้องใช้ความจำมาก

ตัวอย่าง

 

1.) การอ้างเหตุผลนี้ สมเหตุสมผลหรือไม่

เหตุ  1.   ถ้าวันนี้วันจันทร์ แล้วพรุ่งนี้วันอังคาร

2.   วันนี้วันจันทร์

ผล          พรุ่งนี้วันอังคาร

วิธีทำ1 กำหนดให้ p แทนประพจน์  วันนี้วันจันทร์

q แทนประพจน์  พรุ่งนี้วันอังคาร

จะได้  เหตุ   1.   p→q

2.  p

จาก กฎ Modus Ponens

จะได้    ผล       q

ดังนั้น   การอ้างเหตุผลนี้ สมเหตุสมผล

วิธีที่2 การตรวจสอบการเป็นสัจนิรันดร์ได้ โดยจะสมมติให้ประพจน์ เหตุ “แล้ว” ผล มีค่าความจริงเป็นเท็จ แล้วหาข้อขัดแย้ง ดังนี้

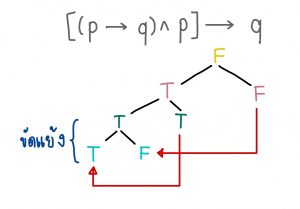
จากรูปข้างบนจะเห็นว่า ประพจน์เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้ สมเหตุสมผล

วิธีที่3 ใช้การสมมูลมาช่วยตรวจสอบ จะได้

ดังนั้น การอ้างเหตุผลนี้ สมเหตุสมผล

2.) การอ้างเหตุผลนี้สมเหตุสมผลหรือไม่

เหตุ      1.  p → q

2.  q → r

3.  p

ผล          r

วิธีทำ1 จาก Law of Syllogism จะได้

เหตุที่ 1  p→q

เหตุที่ 2 q→r

จะได้ ผล p→r

จากนั้น นำ p→r มาพิจารณาต่อ จะได้

พิจารณา p→r

เหตุที่ 3  p

จะได้ ผล r  (Modus Ponens)

ดังนั้น การอ้างเหตุผลนี้ สมเหตุสมผล

วิธีทำ2 ตรวจสอบการเป็นสัจนิรันดร์ โดยสมมติให้ [(p→q)∧(q→r)∧p]→r มีค่าความจริงเป็นเท็จ แล้วเราจะทำการหาจุดที่มันขัดแย้งกัน

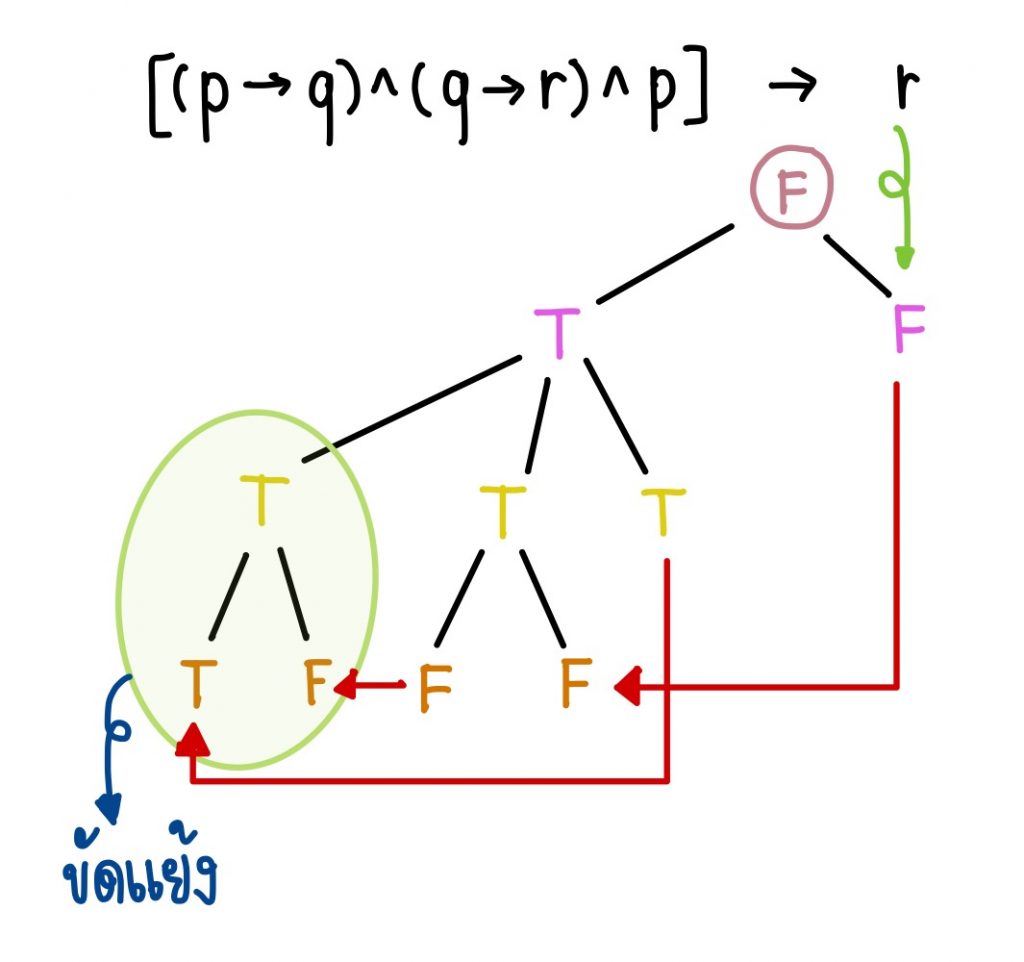
จากรูปข้างบนจะเห็นว่าเป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้ สมเหตุสมผล

3.) พิจารณาการอ้างเหตุผลต่อไปนี้ ว่าสมเหตุสมผลหรือไม่

เหตุ 1.  p ∨ q

 2.       ∼p ∨ r

 3.       ∼r

ผล          p

วิธีทำ เราจะใช้สัจนิรันดร์ ในการตรวจสอบการอ้างเหตุผล

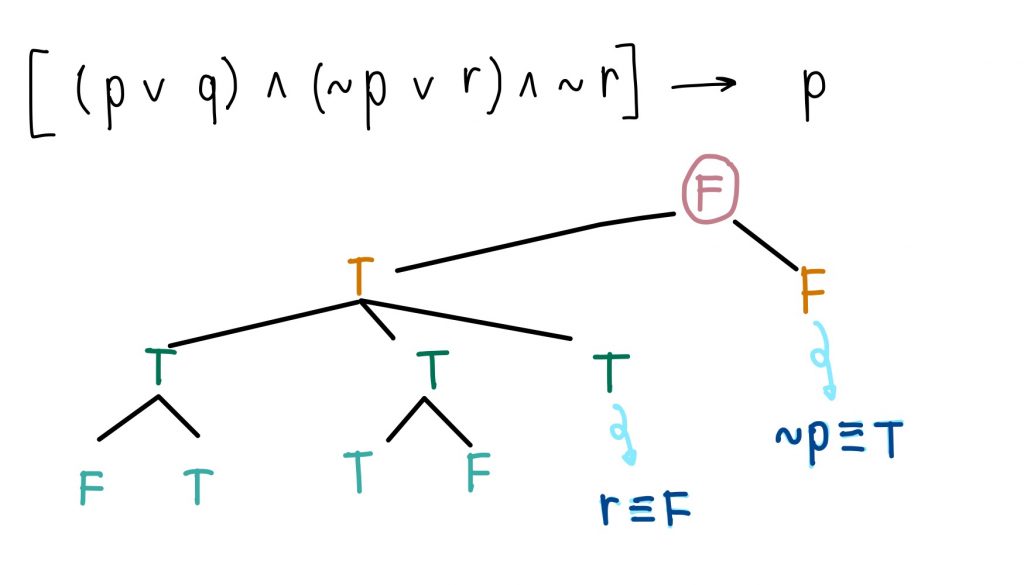
จะเห็นว่า ไม่มีจุดที่ขัดแย้งกัน จะได้ว่า ไม่เป็นสัจนิรันดร์

ดังนั้นการอ้างเหตุผลนี้ ไม่สมเหตุสมผล

4.) พิจารณาการอ้างเหตุผลต่อไปนี้ ว่าสมเหตุสมผลหรือไม่

เหตุที่ 1  p → (q ∨ r)

เหตุที่ 2 ~p ∨ ∼r

ผล         ∼p

วิธีทำ ใช้การตรวจสอบการเป็นสัจนิรันดร์

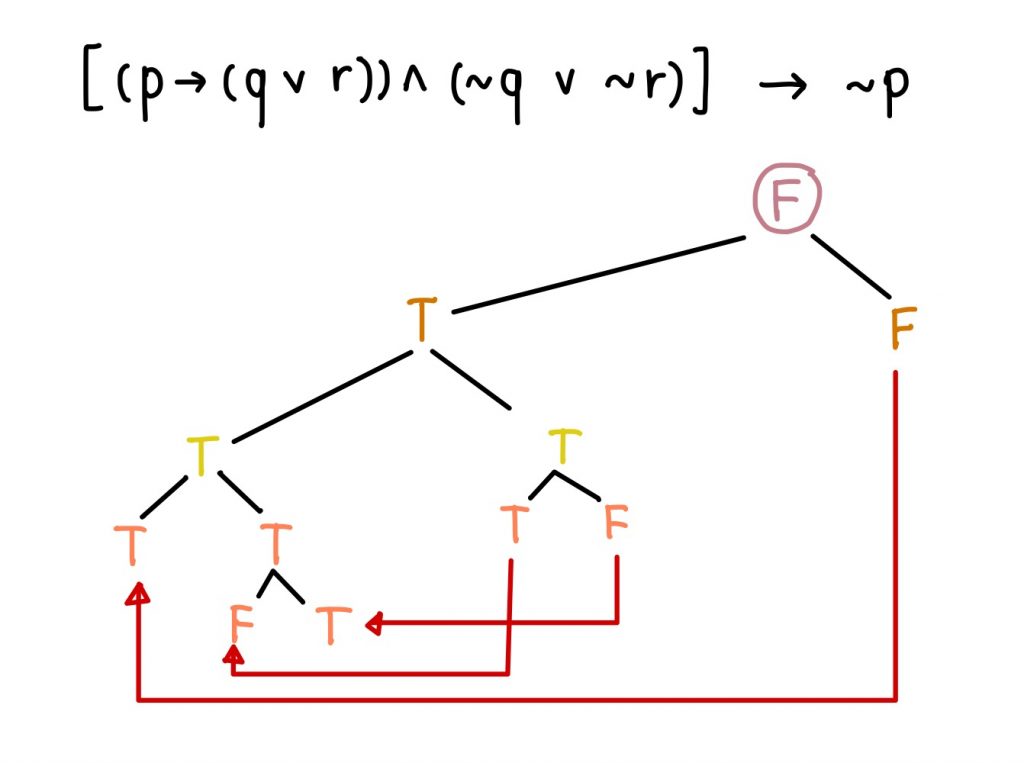
จากรูป จะเห็นว่าไม่มีจุดที่ขัดแย้ง จะได้ว่าไม่เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้ ไม่สมเหตุสมผล

 

จากการยกตัวอย่าง จะเห็นว่าเราสามารถตรวจสอบการอ้างเหตุผลได้หลายวิธี ทั้งตรวจสอบการเป็นสัจนิรันดร์ การสมมูลของประพจน์ และการใช้กฎของการอ้างเหตุผล

การตรวจสอบโดยการใช้ การเป็นสัจนิรันดร์ :

เป็นสัจนิรันดร์ >>> สมเหตุสมผล

ไม่เป็นสัจนิรันดร์ >>> ไม่สมเหตุสมผล

 

การตรวจสอบโดยใช้การสมมูลของประพจน์ :

ประพจน์เป็นจริง(T) >>> สมเหตุสมผล

ประพจน์เป็นเท็จ(F) >>> ไม่สมเหตุสมผล

 

แล้วเราควรจะใช้วิธีไหนล่ะ??

การเลือกใช้นั้นขึ้นอยู่กับโจทย์ บางข้ออาจจะใช้กฎ แต่พอเป็นประพจน์ที่เริ่มซับซ้อนการใช้กฎอาจจะไม่เหมาะ แนะนำให้ใช้วิธีการทดสอบสัจนิรันดร์ค่ะ

แล้วแบบนี้จะรู้ได้ไงว่าข้อไหนควรใช้อะไร??

วิธีที่ได้ผลดีที่สุดคือ เราต้องทำโจทย์เยอะๆค่ะ ยิ่งทำเยอะเรายิ่งเจอโจทย์หลากหลาย เวลาทำข้อสอบจะเราเห็นโจทย์เราจะได้สามารถทำได้เลย ไม่ต้องลองผิดลองถูก ประหยัดเวลาในการทำข้อสอบด้วยนะคะ