พื้นที่ผิวทรงกรวยและลูกบาศก์

พื้นที่ผิวทรงกรวยและลูกบาศก์

การหาพื้นที่ผิวทรงกรวยเเละลูกบาศก์นั้นมักเป็นสิ่งที่เราอาจได้ใช้ในชีวิตประจำวัน ทั้งเรื่องการออกเเบบทางวิศวกรรม หรือสถาปัตยกรรม ที่ต้องนำพื้นที่ผิวมาประเมินค่าใช้จ่ายในการทาสี, การปูกระเบื้อง, หรือเเม้กระทั่งปริมาณการใช้วัสดุในการสร้างชิ้นงานต่าง ๆ

รูปร่างทรงกรวยเเละลูกบาศก์สามารถเห็นได้บ่อยครั้งในชีวิตประจำวัน เช่น โคนไอติม, กรวยจราจร, หมวกปาร์ตี้ ที่มีลักษณะเป็นทรงกรวย เเละลูกเต๋า, ก้อนน้ำเเข็ง ที่มีลักษณะเป็นลูกบาศก์ ซึ่งการหาพื้นที่ผิวทั้งหมดของทรงกรวยเเละลูกบาศก์นั้น มีวิธีง่ายๆ คือ ให้เรามองรูปสามมิติกลายเป็นรูปประกอบของเรขาสองมิติ

พื้นที่ผิวทรงกรวย

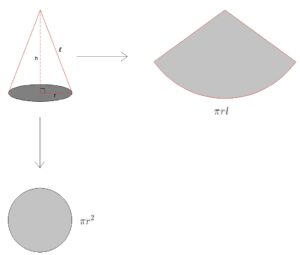
ทรงกรวย คือ รูปทรงเรขาคณิต 3 มิติ ที่มีลักษณะปลายด้านหนึ่งเป็นทรงเเหลม เเละปลายอีกด้านเป็นลักษณะวงกลม โดยภาพคลี่ของทรงกรวยจะมีลักษณะเป็นรูปเรขาสองมิติที่ประกอบด้วย รูปสามเหลี่ยมฐานโค้ง เเละ วงกลม

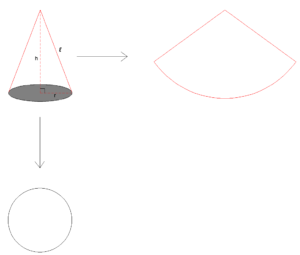
โดยการหาพื้นที่ผิวของทรงกรวยทำได้ดังนี้

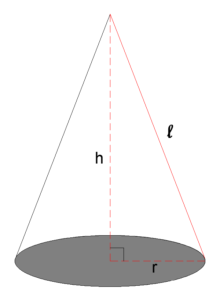
พื้นที่ผิวทรงกรวย = $\large \pi r^{2} + \pi rl$

เมื่อ r คือ ความยาวรัศมีของวงกลมที่เป็นฐาน . h คือ ความสูงของทรงกรวย หรือ เราเรียกว่า “สูงตรง” . l คือ ความสูงเอียงของทรงกรวย หรือ เราเรียกว่า “สูงเอียง”

จากสูตรจะเห็นได้ว่าพื้นที่ผิวของทรงกรวยประกอบด้วยสองส่วนคือ ส่วนที่เป็นพื้นที่ผิวของวงกลมที่เป็นฐาน = $\pi r^{2}$ เเละพื้นที่ผิวของสามเหลี่ยมฐานโค้ง = $\pi rl$ รวมกันทั้งสองส่วนจะได้พื้นที่ผิวทั้งหมดของทรงกรวย

---

ตัวอย่างโจทย์พื้นที่ผิวทรงกรวย

ตัวอย่างที่ 1 จงหาพื้นที่ผิวของทรงกรวยมีความสูงตรง 16 นิ้ว, ความสูงเอียง 22 นิ้ว, เเละมีเส้นผ่านศูนย์กลาง 14 นิ้ว (โดยให้ π = 22/7)

วิธีทำ จากโจทย์วาดรูปได้ดังนี้

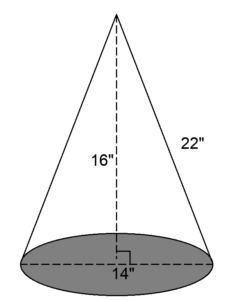
เส้นผ่านศูนย์กลางของทรงกรวยมีความยาว 14 นิ้ว ครึ่งหนึ่งของเส้นผ่านศูนย์กลางคือ รัศมี เเสดงว่ารัศมีความยาว 7 นิ้ว ดังนั้น

พื้นที่ผิวทรงกรวย = $\pi r^{2} + \pi rl$

. = $\frac{22}{7} \cdot 7^{2} + \frac{22}{7}\cdot 7\cdot 22$ . = $22\cdot 7+ 22\cdot 22$ . = $154 + 484$ . = $638$ ตารางนิ้ว

ตอบ พื้นที่ผิวของทรงกรวยมีขนาด 638 ตารางนิ้ว

ตัวอย่างที่ 2 จงหาพื้นที่ผิวของกรวยจราจรที่มีลักษณะทรงกรวยด้านล่างไม่มีส่วนปิดมีความสูงตรง 16 เซนติเมตรเเละมีความสูงเอียง 20 เซนติเมตร (โดยให้ π = 3.14)

วิธีทำ จากโจทย์วาดรูปได้ดังนี้

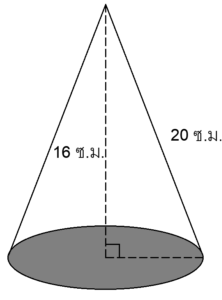โจทย์บอกว่ากรวยจราจรด้านล่างไม่มีส่วนปิดดังนั้น เราจึงไม่ต้องหาพื้นที่ของวงกลมที่เป็นฐานของทรงกรวยจะได้ว่า พื้นที่ผิวของกรวยจราจร = $\pi rl$

จากสูตรจะเห็นได้ว่า ต้องใช้รัศมีของวงกลมเเต่โจทย์ไม่ได้ให้รัศมีมา ซึ่งเราสามารถหารัศมีของวงกลมได้ด้วย ทฤษฎีบทพีทาโกรัส . $c^{2} = a^{2} + b^{2}$ โดยให้ความสูงเอียงเป็นด้านตรงข้ามมุมฉาก = c เเละให้ความสูงตรงเป็น a เเละให้รัศมีเป็น b จะได้ว่า . $20^{2} = 16^{2} + b^{2}$ . $400 = 256 + b^{2}$ . $400 - 256 = b^{2}$ . $144 = b^{2}$ . $b = \sqrt{144} = 12$ รัศมีของวงกลมมีความยาว 12 เซนติเมตร ดังนั้น พื้นที่ผิวของกรวยจราจร = $\pi rl$ . = $3.14 \cdot 12\cdot 20$ . = $753.6$ ตารางเซนติเมตร

ตอบ พื้นที่ผิวของกรวยจราจรมีขนาด 753.6 ตารางเซนติเมตร

---

พื้นที่ผิวทรงลูกบาศก์

ลูกบาศก์ คือ รูปทรงสามมิติที่ประกอบด้วยรูปเรขาคณิตสองมิติที่เป็น สี่เหลี่ยมจตุรัสทั้ง 6 ด้านเเละเเต่ละด้านมีขนาดเเละความยาวเท่ากันทั้งหมด

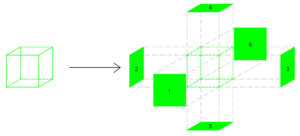
โดยการหาพื้นที่ของทรงลูกบาศก์สามารถทำได้ดังนี้

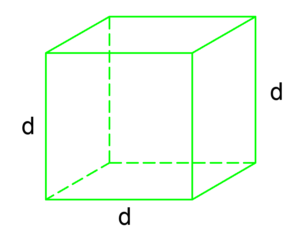
พื้นที่ผิวทรงลูกบาศก์ = $6\cdot d^{2}$ เมื่อ d = ความยาวด้านของทรงลูกบาศก์

จากสูตรจะเห็นได้ว่าเป็นการหาพื้นที่สี่เหลี่ยมจตุรัส = ด้าน x ด้าน เเล้วคูณด้วย 6 เป็นเพราะว่ามีสี่เหลี่ยมจตุรัส 6 ชิ้นประกอบกันทำให้เราได้พื้นที่ผิวทั้งหมดของทรงลูกบาศก์

---

ตัวอย่างโจทย์พื้นที่ผิวทรงลูกบาศก์

ตัวอย่างที่ 3 จงหาพื้นที่ผิวของทรงลูกบาศก์โดยลูกบาศก์มีความยาวด้าน 10 เซนติเมตร

วิธีทำ จากโจทย์จะวาดรูปได้ดังนี้

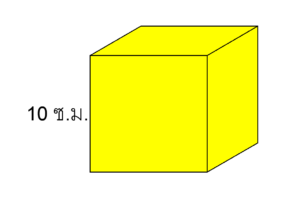ดังนั้นพื้นที่ผิวของทรงลูกบาศก์ = $6\cdot d^{2}$ . = $6\cdot 10^{2}$ . = $6\cdot 100$ . = $600$ ตารางเซนติเมตร

ตอบ พื้นที่ผิวของทรงลูกบาศก์นี้มีขนาด 600 ตารางเซนติเมตร

ตัวอย่างที่ 4 จงหาพื้นที่ผิวรอบนอกเเละพื้นที่ผิวทั้งหมดของทรงลูกบาศก์ต่อไปนี้

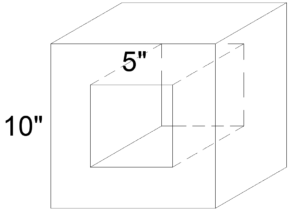
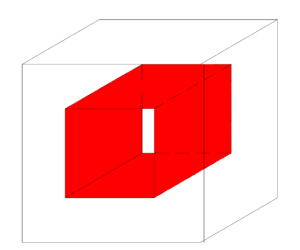
วิธีทำ จากโจทย์จะเห็นได้ว่าทรงสี่เหลี่ยมลูกบาศก์นี้มีช่องสี่เหลี่ยมที่มีความยาวด้าน 5 นิ้วให้เรามองสี่เหลี่ยมนี้เป็นปริซึมสี่เหลี่ยมที่มีความยาวด้าน 5 นิ้ว ยาว 10 นิ้ว เเละโจทย์บอกว่าให้เราหาพื้นที่ผิวรอบนอกของทรงลูกบาศก์ (พื้นที่เเรเงาสีเทา) เเสดงว่าพื้นที่ด้านในของปริซึมสี่เหลี่ยมไม่นำมาคิด

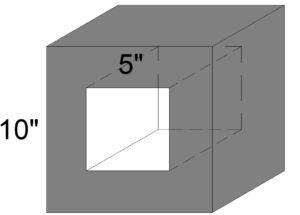
ดังนั้นพื้นที่ผิวของรอบนอกของทรงลูกบาศก์ = พื้นที่ผิวของทรงลูกบาศก์ – (พื้นที่ของสี่เหลี่ยม x 2) . = $(6\cdot d^{^{2}}) - (2\cdot a^{^{2}})$ (โดยให้ความยาวด้านของสี่เหลี่ยม = a) . = $(6\cdot 10^{2}) - (2\cdot 5^{2})$ . = $(6\cdot 100) - (2\cdot 25)$ . = $600 - 50$ . = 550 ตารางนิ้ว

เเละพื้นที่ผิวทั้งหมดของทรงลูกบาศก์คือผลรวมของพื้นที่ผิวรอบนอกของทรงลูกบาศก์ (พื้นที่เเรเงาสีเทา) กับพื้นที่ผิวด้านข้างของปริซึมสี่เหลี่ยม (พื้นที่เเรเงาสีเเดง)

ดังนั้นพื้นที่ผิวทั้งหมดของทรงลูกบาศก์ = พื้นที่ผิวรอบนอกของทรงลูกบาศก์+พื้นที่ผิวด้านข้างของปริซึมสี่เหลี่ยม . = $550 + (4\cdot d\cdot a)$ . = $550 + (4\cdot 10\cdot 5)$ . = $550 + (200)$ . = $750$ ตารางนิ้ว

ตอบ พื้นที่ผิวรอบนอกของทรงลูกบาศก์มีขนาด 550 ตารางนิ้ว เเละพื้นที่ผิวทั้งหมดของทรงลูกบาศก์มีขนาด 750 ตารางนิ้ว

ตัวอย่างที่ 5 จงหาพื้นที่ผิวของทรงลูกบาศก์ต่อไปนี้

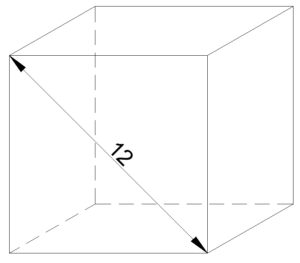
วิธีทำ จากโจทย์จะเห็นได้ว่าเส้นทะเเยงมุมของพื้นที่สี่เหลี่ยมมีความยาว 12 หน่วย เราสามารถหาความยาวด้านของทรงลูกบาศก์ได้ด้วย ทฤษฎีบทพีทาโกรัส

$c^{2} = a^{2} + b^{2}$ $12^{2} = a^{2} + b^{2}$ โดยด้าน a เเละ b เป็นความยาวด้านของทรงลูกบาศก์ซึ่งมีขนาดเท่ากัน มีค่า = d $144 = d^{2} + d^{2}$ $144 = 2d^{2}$

$\frac{144}{2} = d^{2}$ $72 = d^{2}$ $d = \sqrt{72}$ หน่วย

ดังนั้น พื้นที่ผิวของทรงลูกบาศก์ = $6\cdot d^{2}$ . = $6\cdot (\sqrt{72})^{2}$ . = $6\cdot 72$ . = $432$ ตารางหน่วย

ตอบ พื้นที่ผิวของทรงลูกบาศก์นี้มีขนาด 432 ตารางหน่วย

หากน้อง ๆ สามารถคำนวณพื้นที่ผิวของทรงกรวยเเละลูกบาศก์ได้เเล้ว น้อง ๆ สามารถนำไปประยุกต์ใช้ในชีวิตประจำวันได้หลากหลายในอนาคต น้องสามารถศึกษาการหา พื้นที่ผิวทรงกรวยเเละลูกบาศก์ เพิ่มเติมได้ในคลิปวิดีโอด้านล่าง

---

คลิปวิดีโอ พื้นที่ผิวทรงกรวยเเละลูกบาศก์

คลิปวิดีโอนี้ได้รวบรวมวิธีหา พื้นที่ผิวทรงกรวยเเละลูกบาศก์ ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยความรู้ เเละเทคนิครวมถึงการอธิบาย ตัวอย่าง เเละสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย