เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ

supanaree

คณิตศาสตร์, คณิตศาสตร์ เพิ่มเติม, ม.4

Add LINE friends for one click to find article.

เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ

เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะมีความเกี่ยวข้องกับกรณฑ์ในบทความ จำนวนจริงในรูปกรณฑ์ จากที่เรารู้ว่า จำนวนตรรกยะคือจำนวนที่สามารถเขียนอยู่ในรูปเศษส่วนของจำนวนเต็มได้ เช่น $\frac{2}3{}$ , $\frac{5}{4}$ , $\frac{1}{2}$ , 2 , 3 เป็นต้น ดังนั้นเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ ก็คือจำนวนจริงใดๆยกกำลังด้วยจำนวนที่สามารถเขียนในรูปเศษส่วนของจำนวนเต็ม เช่น $\mathrm{5^{\frac{2}{3}}}$ , $3^{\frac{5}{4}}$ เป็นต้น

โดยนิยามของเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ คือ

$เลขยกกำลัง$ เมื่อ k และ n เป็นจำนวนเต็ม และ n > 1

เราเรียก

$เลขยกกำลัง$ ว่า เลขยกกำลัง

$a$ คือ เลขฐาน

$\frac{k}{n}$ คือ เลขชี้กำลัง

ตัวอย่าง

$เลขยกกำลัง$ = $\sqrt[3]{5^{2}}$

$เลขยกกำลัง$ = $\sqrt[4]{3^{5}}$ = $3\sqrt[4]{3}$

สมบัติของ เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ

ให้ a, b เป็นจำนวนจริง และ m, n เป็นจำนวนเต็ม

1.) $เลขยกกำลัง$

ตัวอย่าง

$เลขยกกำลัง$

$(2^x)(2^y)=2^{x+y}$

2.) $เลขยกกำลัง$ , $a\neq 0$

ตัวอย่าง

$เลขยกกำลัง$

3.) $เลขยกกำลัง$

ตัวอย่าง

$(7^3)^2=7^{3\times 2}=7^6$

4.) $เลขยกกำลัง$

ตัวอย่าง

$เลขยกกำลัง$

5.) $เลขยกกำลัง$

ตัวอย่าง

$\frac{3^2}{5^2}=(\frac{3}{5})^2$

ตัวอย่างการใช้งานสมบัติและนิยาม

ตัวอย่างต่อไปนี้จะเป็นการเขียนเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะให้อยู่ในรูปอย่างง่าย

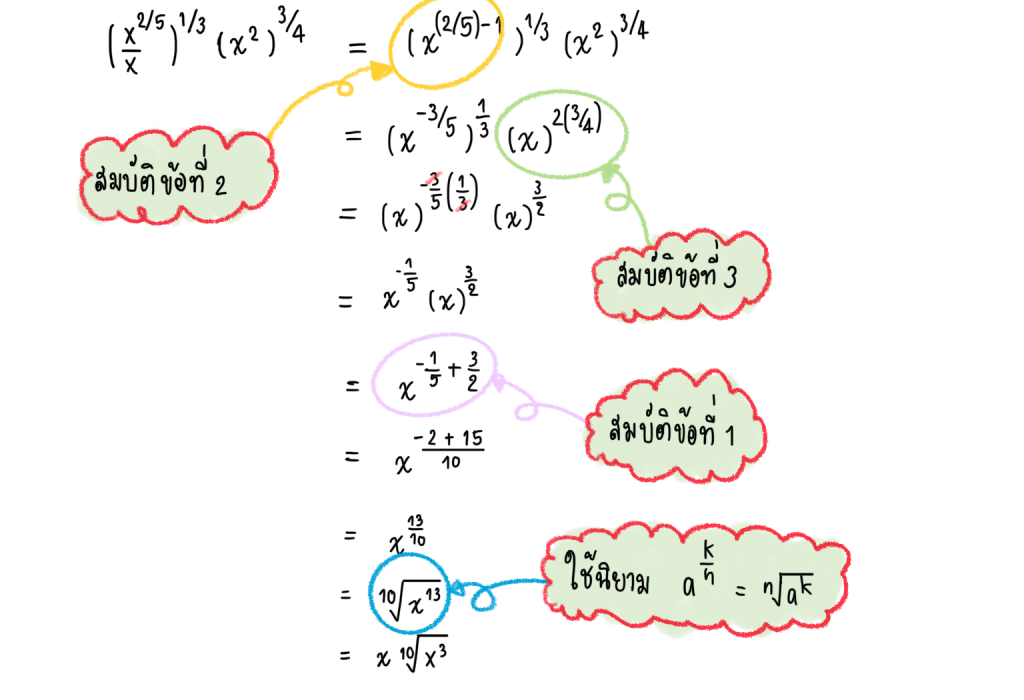
การบวก ลบ คูณ และหาร เลขยกกำลัง

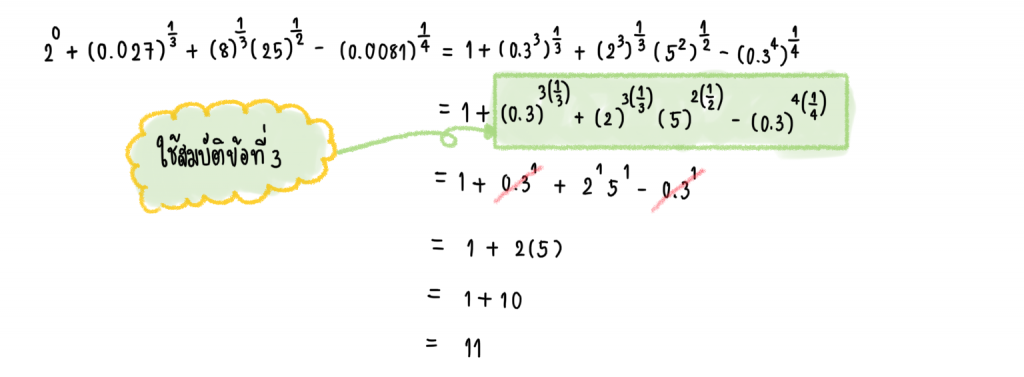
ตัวอย่างนี้เป็นวิธีการบวก ลบ คูณ หาร เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ

เราจะหาค่าของ $2^{0}+(0.027)^{\frac{1}{3}}+(8)^{\frac{1}{3}}(25)^{\frac{1}{2}}-(0.0081)^{\frac{1}{4}}$

การที่ตัวเลขเหล่านี้จะบวกลบกันได้ง่ายขึ้นอาจจะต้องทำให้เลขชี้กำลังหายหรือทำให้เป็นจำนวนเต็ม

เราลองมาจัดรูปใหม่ โดยการพิจารณาตัวเลขต่อไปนี้

$2^{0} = 1$

$0.027 = 0.3^3$

$8=2^3$

$25=5^2$

$0.0081=0.3^4$

ดังนั้นจะได้รูปใหม่ได้เป็น

วิดีโอเพิ่มเติม

การทำแบบฝึกหัดในบทความนี้ไม่มีวิธีที่แน่นอนตายตัวบางข้ออาจจะต้องใช้สมบัติหลายอย่าง บางข้ออาจจะต้องใช้นิยามช่วย แบบฝึกหัดเหล่านี้ต้องอาศัยการสังเกตและอาศัยการฝึกทำแบบฝึกหัดบ่อยๆ เพื่อที่น้องๆจะได้เจอแบบฝึกหัดหลายรูปแบบและจะทำให้น้องๆพร้อมสำหรับการสอบในสนามสอบต่างๆอีกด้วย

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

ประวัติความเป็นมาของวรรณคดีคำสอน เรื่องสุภาษิตพระร่วง

สุภาษิตพระร่วง คนไทยนิยมใช้สุภาษิตสั่งสอนลูกหลานกันมาตั้งแต่สมัยก่อนจนถึงปัจจุบัน เชื่อว่าน้อง ๆ หลายคนก็คงจะเคยได้ยินสุภาษิตกันมาไม่มากก็น้อย ดังนั้นบทเรียนในวันนี้จะพาน้อง ๆ ไปเรียนรู้ประวัติความเป็นมาของสุภาษิตพระร่วง วรรณคดีอันทรงคุณค่าและเป็นวรรณคดีเล่มแรกที่แต่งคำประพันธ์เป็นร่ายโบราณแบบร่ายสุภาพ ไปศึกษาเรื่องนี้พร้อม ๆ กันเลยค่ะ ความเป็นมาของสุภาษิตพระร่วง สุภาษิตพระร่วง เป็นวรรณคดีคำสอนที่ทรงคุณค่าที่มีมาอย่างยาวนาน มีชื่อเรียกอีกอย่างหนึ่งว่า สุภาษิตบัณฑิตพระร่วง คำว่า พระร่วง ทำให้คนเข้าใจว่าอาจจะเป็นคำสอนของกษัตริย์สักคนที่มีนามว่า พระร่วง

สมบัติการบวกจำนวนจริง

สมบัติการบวกจำนวนจริง สมบัติการบวกจำนวนจริง เป็นสมบัติที่น้องๆต้องรู้ เพราะเป็นรากฐานของวิชาคณิตศาสตร์และน้องๆจะต้องใช้สมบัติพวกนี้ในการเรียนคณิตศาสตร์ในระดับที่สูงขึ้น สมบัติการบวกของจำนวนจริง มีทั้งหมด 5 ข้อ ดังนี้ 1.) สมบัติปิดการบวก สมบัติปิดการบวก คือ การที่เรานำจำนวนจริง 2 ตัวมาบวกกัน เราก็ยังได้ผลลัพธ์เป็นจำนวนจริงเหมือนเดิม เช่น 1 + 2 = 3 จะเห็นว่า

ฟังก์ชันลอการิทึม

ฟังก์ชันลอการิทึม ฟังก์ชันลอการิทึม คือฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียล จากที่ฟังก์ชันเอกซ์โพเนนเชียลคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์ที่ส่งจากจำนวนจริงไปยังจำนวนจริงบวก โดยที่ ดังนั้นฟังก์ชันดังกล่าวซึ่งเป็นฟังก์ชันผกผันของเอกซ์โพเนนเชียล ก็คือ คู่อันดับ (y, x) หรืออาจจะบอกได้อีกแบบคือ คู่อันดับ (x, y) ซึ่งเป็นความสัมพันธ์จากจำนวนจริงบวกไปยังจำนวนจริง โดยที่ จัดรูปใหม่ ได้เป็น (อ่านว่าล็อก x ฐาน

มารู้จักกับ Passive Modals

สวัสดีค่านักเรียนชั้นม.6 ที่น่ารักทุกคน วันนี้เราจะไปดู ” Passive Modals” ที่ใช้บ่อยพร้อม เทคนิคการจำและนำไปใช้ และทำแบบฝึกหัดท้ายบทเรียน กันค่า Let’s go! ไปลุยกันโลดเด้อ Passive Modals คืออะไรเอ่ย Passive Modals คือ กลุ่มของ Modal verbs ที่ใช้ในโครงสร้าง

การใช้ Question Words

สวัสดีค่ะนักเรียนชั้น ป.5 ที่น่ารักทุกคน วันนี้ครูจะพาเรียนรู้เกี่ยวกับ Question Words ที่รวมทั้งรูปแบบกริยาช่วยนำหน้าประโยค และรูปแบบ Wh-questions กันนะคะ พร้อมกันหรือยังเอ่ย ถ้าพร้อมแล้วก็ ไปลุยกันเลย Question words ขึ้นต้นด้วยกริยาช่วย ทบทวนกริยาช่วยสักนิด Helping verb หรือ Auxiliary verb

Describing People: การบรรยายบุคคลในภาษาอังกฤษ

สวัสดีน้องๆ ม. 2 ทุกคนครับ วันนี้เราจะมาเรียนรู้วิธีการบรรยายลักษณะบุคคลเป็นภาษาอังกฤษกันครับ ถ้าพร้อมแล้วไปเริ่มกันเลย!

เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ

สารบัญ

เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ

สมบัติของ เลขยกกำลัง ที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ

ตัวอย่างการใช้งานสมบัติและนิยาม

การบวก ลบ คูณ และหาร เลขยกกำลัง

วิดีโอเพิ่มเติม

แค่ 10 นาที ก็เข้าใจได้

แนะนำ

แชร์

ประวัติความเป็นมาของวรรณคดีคำสอน เรื่องสุภาษิตพระร่วง

สมบัติการบวกจำนวนจริง

ฟังก์ชันลอการิทึม

มารู้จักกับ Passive Modals

การใช้ Question Words

Describing People: การบรรยายบุคคลในภาษาอังกฤษ

NockAcademy

ติดต่อ

เกี่ยวกับเรา

ความช่วยเหลือ

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1