การดำเนินการของเซต คือ การนำเซตที่มีอยู่แล้วมาดำเนินการเพื่อให้ได้เซตใหม่ เราจะใช้แผนภาพเวนน์-ออยเลอร์เพื่อช่วยให้เห็นภาพและเข้าใจได้ง่ายขึ้น

การเขียนแผนภาพ เราจะใช้เอกภพสัมพัทธ์ U ด้วยรูปสี่เหลี่ยมผืนผ้า ส่วนเซตที่อยู่ใน U เราอาจจะเขียนแทนด้วยวงกลม วงรี หรือรูปอื่นๆ เช่น

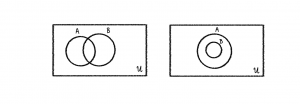
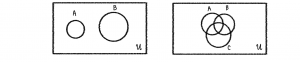
การยูเนียน (union)

เราจะใช้สัญลักษณ์ ∪ แทนการยูเนียน

A ∪ B อ่านว่า A ยูเนียน B คือการเอาสมาชิกทั้งหมดในเซต A รวมกับ สมาชิกทั้งหมดในเซต B

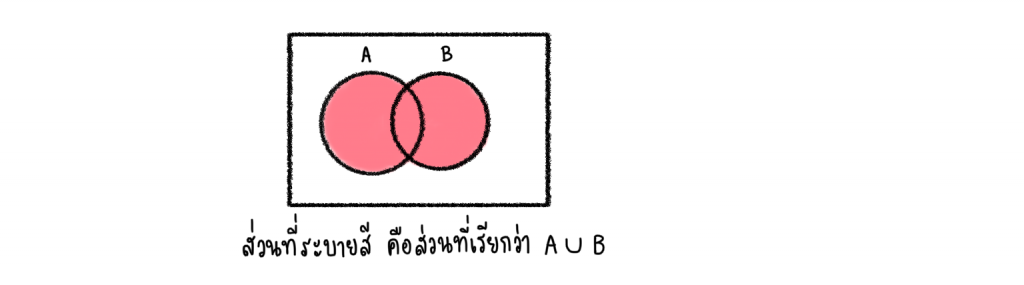
เช่น ให้ A = {1,2,3} B = {1,a,b,c} จะได้ A∪B = {1,2,3,a,b,c}

สมบัติของการยูเนียน

ให้ A,B,C เป็นเซตย่อยของเอกภพสัมพัทธ์

1.) A∪Ø = A

2.) A∪B = B∪A

3.) A∪(B∪C) = (A∪B)∪C

4.) A∪A = A

การอินเตอร์เซกชัน (intersection)

เราจะใช้สัญลักษณ์ ∩ แทนการอินเตอร์เซกชัน

A∩B อ่านว่า A อินเตอร์เซกชัน B คือ เซตที่สร้างมาจากส่วนที่ A กับ B มีสมาชิกร่วมกัน

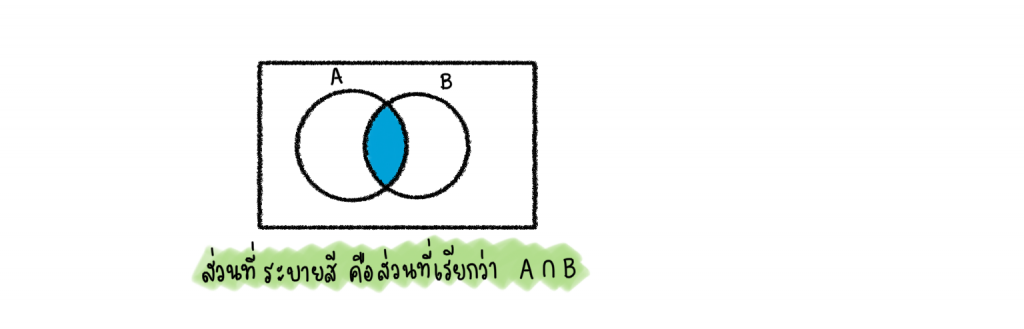
เช่น A = {1,2,3,4,5}  B = {2,4,5,a,b} จะได้ว่า A∩B = {2,4,5}

A∩B คือส่วนที่ A กับ B ซ้ำกัน

สมบัติของการอินเตอร์เซกชัน

ให้ A,B,C เป็นเซตย่อยของเอกภพสัมพัทธ์

1.) A∩Ø = Ø

2.) A∩U = A

3.) A∩B = B∩A

4.) (A∩B)∩C = A∩(B∩C) 

5.) A∩A = A

ตัวอย่างการยูเนียนและอินเตอร์เซกชัน

ให้ A,B,C เป็นเซตย่อยของเอกภพสัมพัทธ์ U

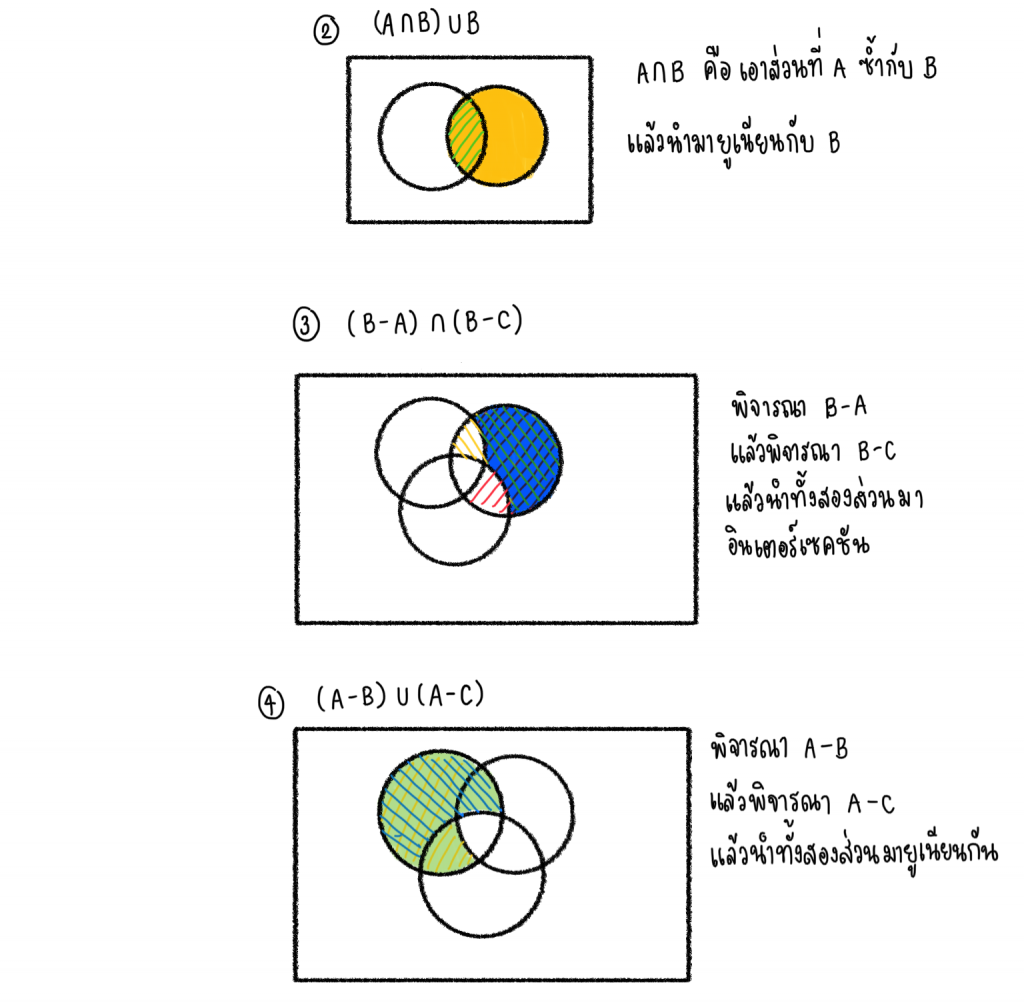
ให้แรเงาตามที่โจทย์กำหนด

1.) A∪B

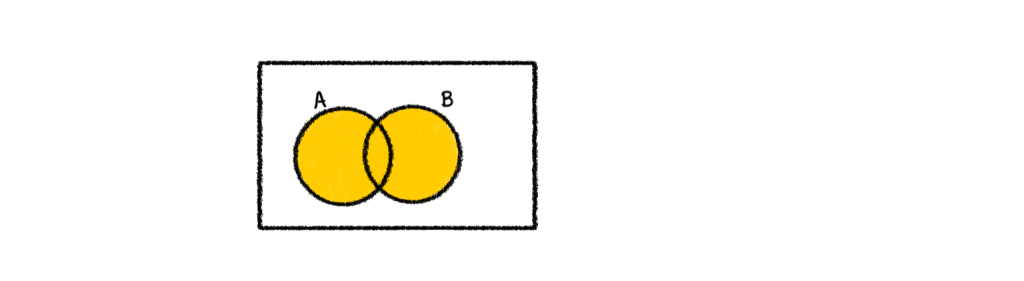
2.) A∩B

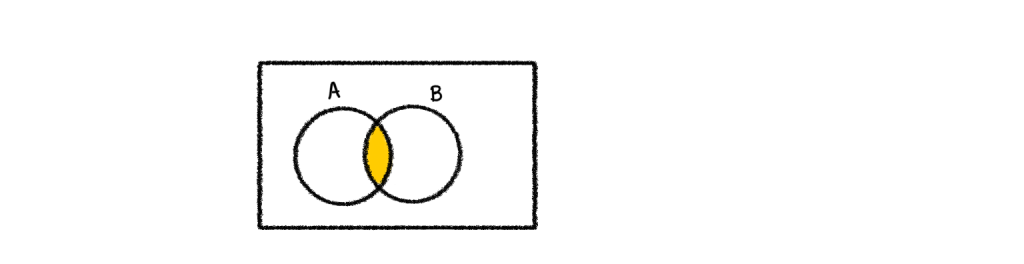
3.) (A∩B)∪C

เราจะทำในวงเล็บก่อน

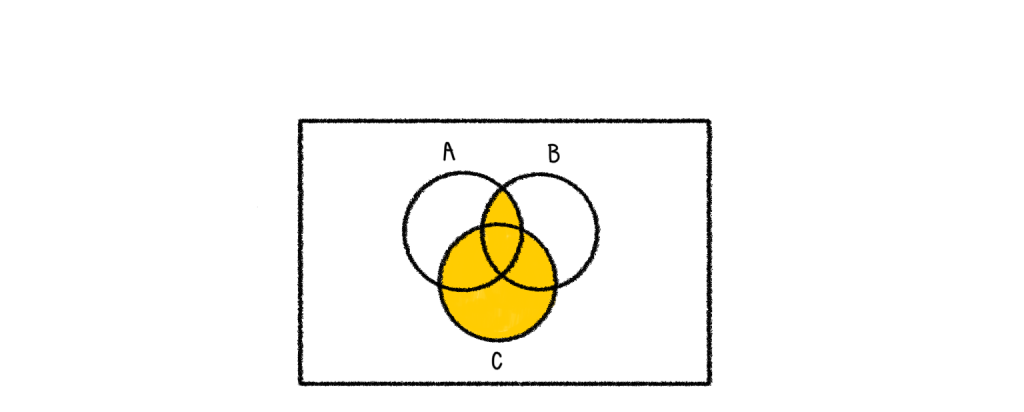
4.) A∩B∩C

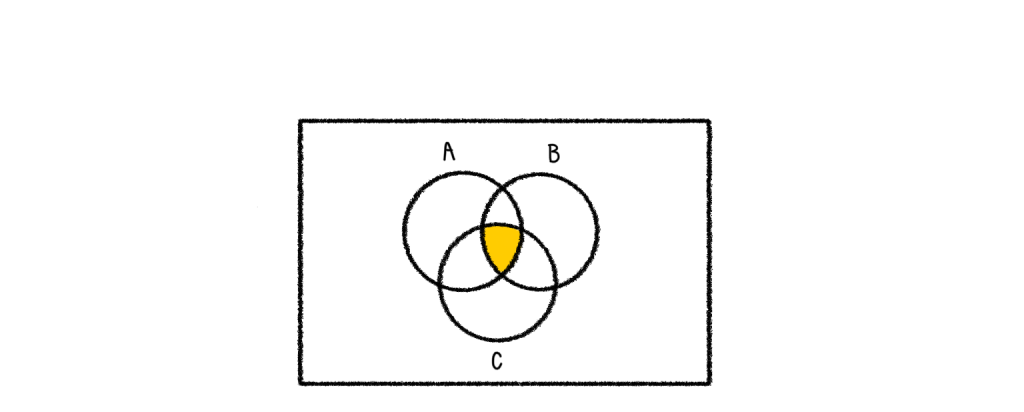
ส่วนเติมเต็ม (complement)

ให้A เป็นเซตย่อยของ U เราจะใช้ A′ แทน ส่วนเติมเต็มของ A

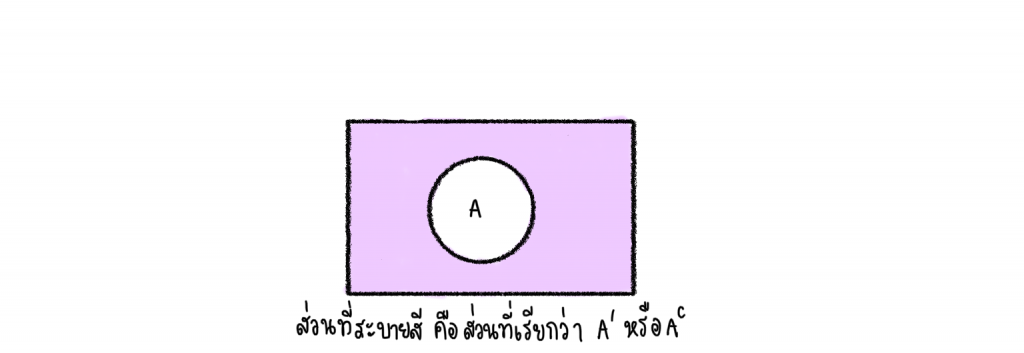
พูดให้เข้าใจง่าย A′ ก็คือ ส่วนที่ไม่ใช่ A 

สมบัติของส่วนเติมเต็ม

ให้ A และ B เป็นเซตย่อยของ U

1.) (A′)′ = A

2.) A∩A′ = Ø

3.) A∪A′ = U

4.) (A∪B)′ = A′∩B′

5.) (A∩B)′ = A′∪B′

6.) Ø′ = U

7.) U′ = Ø

ผลต่างเซต (difference)

ให้ A และ B เป็นเซตย่อยของ U 

ผลต่างของเซต A กับเซต B เขียนแทนด้วย A-B 

A-B คือเซตที่มีสมาชิกของA แต่ไม่มีสมาชิกของ B

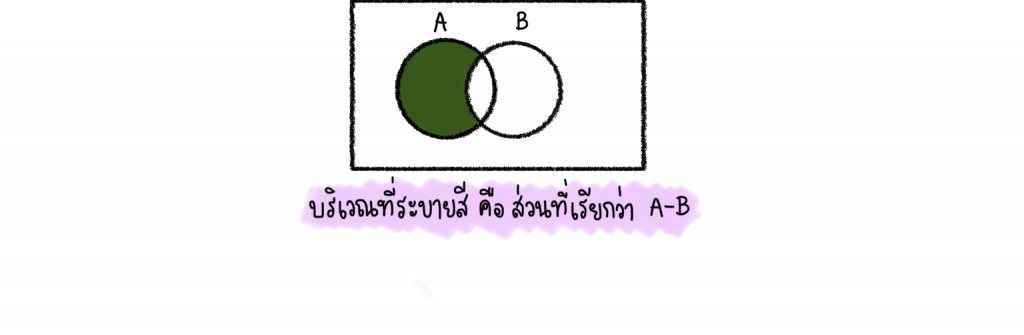
trick!! A-B ก็คือ เอาA ไม่เอา B

เช่น A = {1,2,3,4,a,b,c,d} B = {3,4,c,d,e,f}

จะได้ว่า A-B = {1,2,a,b} และ B-A = {e,f}

ภาพประกอบตัวอย่าง

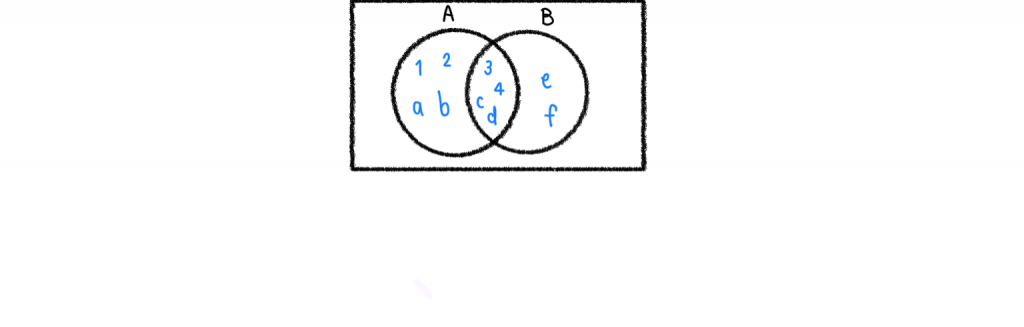
สมบัติที่ควรรู้

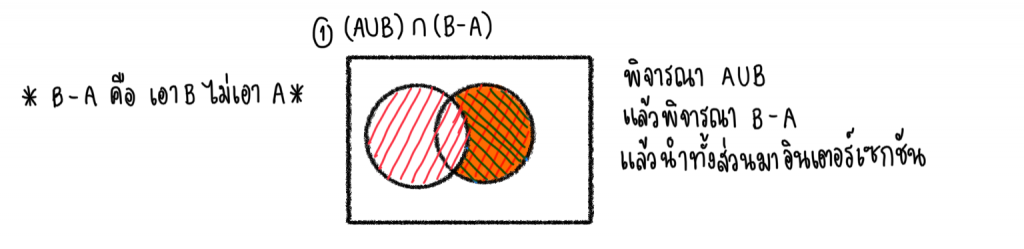
ตัวอย่าง

ระบายสีตามที่โจทย์กำหนดให้

2.) ให้เอกภพสัมพัทธ์ U = {0,1,2,3,4,5,6,7,8,10}

A ={0,1,3,5,7,9},  B = {0,2,4,6,8,10}

C = {0,3,5,6,8}

จงหา

1.) (A∪B′)∪C

วิธีทำ จากโจทย์ จะได้ว่า (A∪B′)∪C = (A∪C)∪(B′∪C)

พิจารณา A∪C 

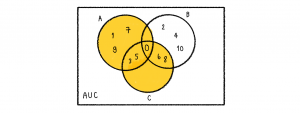
จากนั้นพิจารณา B′∪C

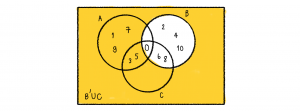
และนำทั้งสองมายูเนียนกัน จะได้

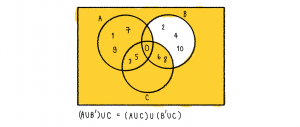
ดังนั้น (A∪B′)∪C = {0,1,3,5,6,7,8,9}

2.) (A∪C)∩(A∪B)

วิธีทำ พิจารณา (A∪C) จะได้

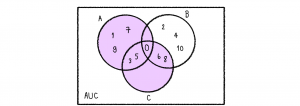
จากนั้นพิจารณา (A∪B) จะได้

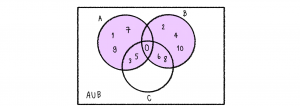
จากนั้นก็นำทั้งสองมาอินเตอร์เซกชัน เราจะได้ส่วนที่ซ้ำกันดังนี้

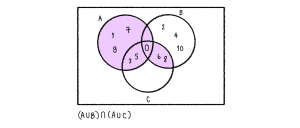
ดังนั้น (A∪C)∩(A∪B) = {0,1,3,5,6,7,8,9}

3.) A-(B∩C)

วิธีทำ พอจารณา (B∩C) จะได้

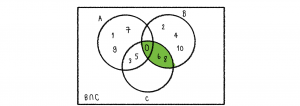
จากนั้นพิจารณา A-(B∩C) จะได้

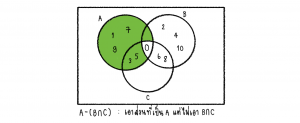
ดังนั้น A-(B∩C) = {1,3,5,7,9}