การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่ง
การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่ง คือ การนำเสนอข้อมูลที่ได้มีการเก็บรวบรวมข้อมูลไว้โดยใช้รูปสี่เหลี่ยมมุมฉาก ซึ่งเเต่ละรูปมีความกว้างเท่ากัน เเละใช้ความสูงหรือความยาวเเสดงปริมาณของข้อมูล เเต่จุดเริ่มต้นจะต้องเริ่มในระดับเดียวกันเสมอ อาจอยู่ในเเนวตั้งหรือเเนวนอนก็ได้
การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่งเปรียบเทียบ คือ การนำเสนอข้อมูลโดยเปรียบเทียบข้อมูลตั้งเเต่ 2 ชุดขึ้นไปในแผนภูมิเดียวกัน โดยมีเเท่งสี่เหลี่ยมที่เเสดงข้อมูลชนิดเดียวกันอยู่ด้วยกันเป็นชุดๆ เเละมีสีหรือเเรเงาในเเท่งสี่เหลี่ยมต่างกัน เเละระบุไว้บนเเผนภูมิด้วยว่าสีหรือเเรเงานั้น ๆ เป็นข้อมูลของอะไร
ตัวอย่างของแผนภูมิเเท่งเปรียบเทียบ
ส่วนประกอบของเเผนภูมิแท่ง:
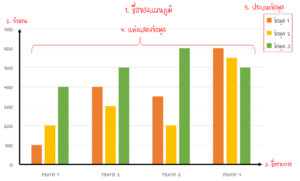
1. ชื่อแผนภูมิ
2. จำนวน
3. ชื่อรายการ
4. แท่งเเสดงข้อมูล
5. ประเภทของข้อมูล
↓
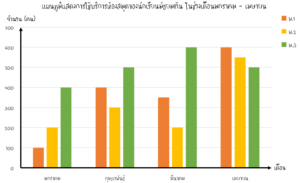
โดยแผนภูมิด้านบนเเสดงถึงจำนวนนักเรียนที่เข้ามาใช้บริการในห้องสมุดเเบ่งกลุ่มเป็นเดือน เเละมีเเท่งเเสดงข้อมูล สีส้ม, สีเหลือง, เเละสีเขียว เเสดงข้อมูลของนักเรียนชั้น ม.1, ม.2, เเละ ม.3 ตามลำดับ ซึ่งแผนภูมิที่ได้น้อง ๆ สามารถนำไปแปลความหมายเป็นข้อมูลต่าง ๆ ได้
ตัวอย่างการเเปรความหมายเเผ่นภูมิเเท่ง
ตัวอย่างที่ 1 จากเเผนภูมิด้านบน จำนวนนักเรียนชั้น ม.3 ที่เข้ามาใช้บริการห้องสมุดในช่วงเดือนมกราคม ถึง มีนาคม มีทั้งหมดกี่คน
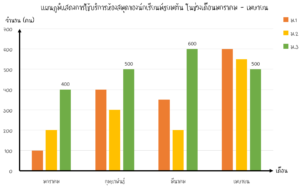
วิธีทำ จากเเผนภูมิเเท่งจำนวนนักเรียนชั้น ม.3 (เเท่งสีเขียว) ที่เข้ามาใช้บริการห้องสมุดตั้งเเต่เเต่เดือน มกราคม ถึง เมษายน มีค่าเท่ากับ
= จำนวนนักเรียนชั้น ม.3 เดือนมกราคม + เดือนกุมภาพันธ์ + เดือนมีนาคม + เดือนเมษายน
= 400 + 500 + 600 + 500
ตอบ ทั้งหมด 2,000 คน
ตัวอย่างที่ 2 จากเเผนภูมิด้านบน เดือนที่มีจำนวนนักเรียนเข้ามาใช้บริการมากที่สุด คือเดือนอะไร เเละจำนวนเท่าใด
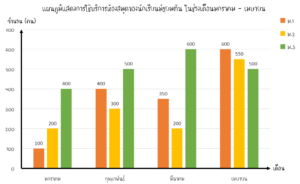
วิธีทำ จากเเผนภูมิเเท่งจำนวนนักเรียนที่เข้ามาใช้บริการในเเต่ละเดือนมีดังนี้
เดือนมกราคม จำนวนนักเรียนชั้น ม.1 + ม.2 + ม.3 = 100 + 200 + 400 = 700 คน
เดือนกุมภาพันธ์ จำนวนนักเรียนชั้น ม.1 + ม.2 + ม.3 = 400 + 300 + 500 = 1,200 คน
เดือนมีนาคม จำนวนนักเรียนชั้น ม.1 + ม.2 + ม.3 = 350 + 200 + 600 = 1,150 คน
เดือนเมษายน จำนวนนักเรียนชั้น ม.1 + ม.2 + ม.3 = 600 + 550 + 500 = 1,650 คน
ตอบ เดือนเมษายน จำนวน 1,650 คน
ตัวอย่างที่ 3 จากเเผนภูมิด้านบน จำนวนนักเรียนชั้น ม.2 ที่เข้ามาใช้บริการห้องสมุดในเดือนกุมภาพันธ์มีจำนวนมากกว่าหรือน้อยกว่าเดือนมีนาคมเท่าใด
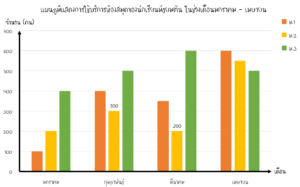
วิธีทำ จากเเผนภูมิเเท่งจำนวนนักเรียนชั้นม.2 (เเท่งสีเหลือง) ที่เข้ามาใช้บริการห้องสมุดในเดือนกุมภาพันธ์ทั้งหมด 300 คน เเละในเดือนมีนาคมทั้งหมด 200 คน
ดังนั้น จำนวนนักเรียนในเดือนกุมภาพันธ์ – จำนวนนักเรียนในเดือนมีนาคม = 300 – 200 คน
= 100 คน
ตอบ มีจำนวนมากกว่าทั้งหมด 100 คน
ตัวอย่างที่ 4 จากเเผนภูมิด้านบน ตั้งเเต่เดือนมกราคม ถึง เมษายน จำนวนเฉลี่ยของนักเรียนชั้น ม.1 ที่เข้ามาใช้บริการห้องสมุดในเเต่ละเดือนเป็นเท่าใด
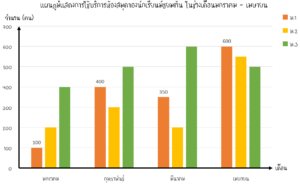
วิธีทำ จากแผนภูมิเเท่ง จำนวนนักเรียนชั้น ม.1 (เเท่งสีส้ม) ที่เข้ามาใช้บริการห้องสมุดในเเต่ละเดือนมีจำนวนดังนี้
เดือนมกราคม จำนวน 100 คน
เดือนกุมภาพันธ์ จำนวน 400 คน
เดือนมีนาคม จำนวน 350 คน
เดือนเมษายน จำนวน 600 คน
โดยทั้ง 4 เดือน มีจำนวนนักเรียนที่เข้ามาใช้บริการทั้งหมดรวมกัน = 100 + 400 + 350 + 600 = 1450 คน
ดังนั้น จำนวนเฉลี่ยของนักเรียนชั้น ม.1 มีค่า = จำนวนทั้งหมดรวมกัน/จำนวนเดือน
= 1,450 คน/4 เดือน
= 362.5 คน/เดือน
ตอบ จำนวนเฉลี่ยของนักเรียนชั้น ม.1 ที่เข้าใช้บริการห้องสมุดมีค่าเท่ากับ 362.5 คน/เดือน
ตัวอย่างที่ 5 จากเเผนภูมิเเท่งด้านบน จำนวนนักเรียนชั้น ม.3 มีจำนวนเป็นร้อยละเท่าใดของจำนวนนักเรียนทั้งหมดที่มาใช้บริการในเดือนมีนาคม
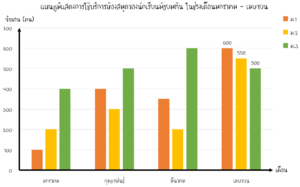
วิธีทำ จากตัวอย่างที่ 2 จำนวนนักเรียนทั้งหมดที่ใช้บริการห้องสมุดในเดือนมีนาคมมีจำนวน 1150 คน
เเละจำนวนนักเรียนชั้น ม.3 ที่มาใช้บริการห้องสมุดในเดือนมีนาคมมีจำนวน 600 คน
ดังนั้น ร้อยละของจำนวนนักเรียนชั้น ม.3 ต่อจำนวนนักเรียนทั้งหมดที่มาใช้บริการในเดือนมีนาคมมีค่า
= (จำนวนนักเรียนชั้น ม.3/จำนวนนักเรียนทั้งหมด) x 100
= (600/1150) x 100
= 52.17
ตอบ ร้อยละ 52.17 ของนักเรียนทั้งหมดที่มาใช้บริการในเดือนมีนาคม
เมื่อเราเเปลความหมายข้อมูลได้ เราสามารถนำข้อมูลต่าง ๆ มาวิเคราะห์ต่อไปในด้านอื่น ๆ ได้เพื่อต่อยอดหรือเเก้ไขปัญหาต่างๆ ด้วยการตั้งคำถามง่าย ๆ เช่น ทำไมช่วงเดือนเมษายนจึงมีนักเรียนเข้าใช้บริการห้องสมุดเยอะที่สุด อาจเป็นเพราะว่าใกล้ช่วงสอบนักเรียนจึงเข้าไปใช้บริการห้องสมุดเยอะ อาจจะเกิดปัญหาเก้าอี้ไม่พอในอนาคตได้ ดังนั้นทางห้องสมุดอาจจะเเก้ไขปัญหาด้วยการ เพิ่มจำนวนโต๊ะเเละเก้าอี้เพื่อให้มีที่นั่งเพียงพอกับนักเรียนที่เข้ามาใช้บริการ
บทความนี้ได้รวบรวมเนื้อหาของ การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่ง จะเห็นได้ว่ามีส่วนสำคัญในการเเก้ปัญหาที่จะเกิดขึ้นในอนาคตได้ หากวิเคราะห์ข้อมูลได้อย่างมีประสิทธิภาพ
ในส่วนของการสร้างเเผนภูมิเเท่งเเละตัวอย่างการเเปรความหมายน้อง ๆ สามารถศึกษาเพิ่มเติมได้จากวิดีโอนี้
คลิปวิดีโอ การนำเสนอข้อมูลเเละการเเปรความหมายข้อมูลด้วยเเผนภูมิเเท่ง
คลิปวิดีโอนี้ได้รวบรวมวิธี การนำเสนอข้อมูลและแปลความหมายข้อมูลด้วยแผนภูมิแท่ง ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยความรู้ เเละเทคนิครวมถึงการอธิบาย ตัวอย่าง เเละสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย