อสมการ

อสมการ คือการไม่เท่ากัน ซึ่งการไม่เท่ากันนั้น สามารถเป็นไปได้ทั้ง มากกว่า, น้อยกว่า , มากกว่าหรือเท่ากับ และน้อยกว่าหรือเท่ากับ เนื้อหาในบทความนี้จะเกี่ยวข้องกับเรื่องช่วงของจำนวนจริงด้วย น้องๆสามารถดูบทความเรื่องช่วงของจำนวนจริงเพิ่มเติมได้ที่ >>>ช่วงของจำนวนจริง<<<

การแก้อสมการจะทำคล้ายๆกับสมการ มีเป้าหมายเดียวกันก็คือ หาค่าตัวแปรตัวแปรหนึ่งสมมติให้เป็น x แต่คำตอบจะต่างกับสมการ การแก้สมการหาค่า x เราจะได้ค่า x มา โดยระบุชัดเจนเลยว่า x มีค่าเท่ากับเท่านี้ แต่สำหรับอสมการคำตอบจะเป็นช่วง เช่น แก้อสมการแล้วได้คำตอบว่า x > 3 แสดงว่า x ที่มากกว่า 3 นั้นเป็นคำตอบของอสมการทั้งหมดเลย

สมบัติที่ควรรู้ของอสมการ

ให้ a, b เป็นจำนวนจริงใดๆ

1.) ถ้า a > b แล้ว -a < -b

คำอธิบายเพิ่มเติม ถ้า เรามีจำนวนจริงที่ 2 ตัว ที่ไม่เท่ากัน เมื่อคูณด้วยจำนวนจริงลบเข้าไปทั้งสองฝั่งของอสมการ จะทำให้เครื่องหมายของอสมการเปลี่ยนไป

ตัวอย่าง  2 < 3  สมมติคูณด้วย -3 ทั้งสองข้างของอสมการ จะได้ว่า 2(-3) > 3(-3)  ⇒ -6 > -9

เห็นได้ชัดเลยว่า เมื่อคูณลบไปแล้ว เครื่องหมายจะเปลี่ยน

ตัวอย่างการแก้อสมการ

1.) จงหาค่า x เมื่อ x + 5 > 2x -2  พร้อมกับวาดเส้นจำนวน

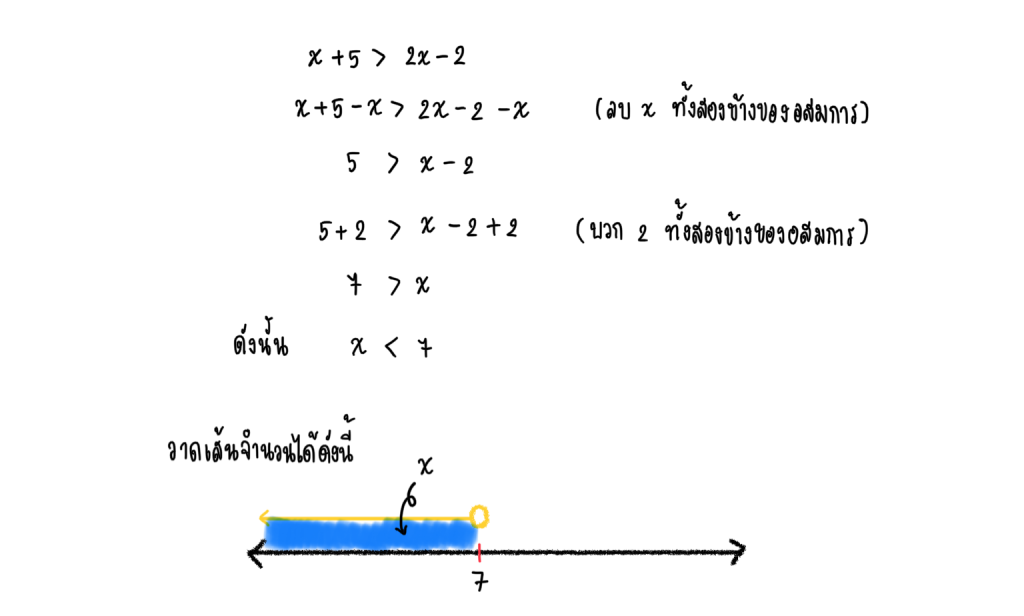
2.) จงหาค่า x เมื่อ x² -3 > 1 พร้อมกับวาดเส้นจำนวน

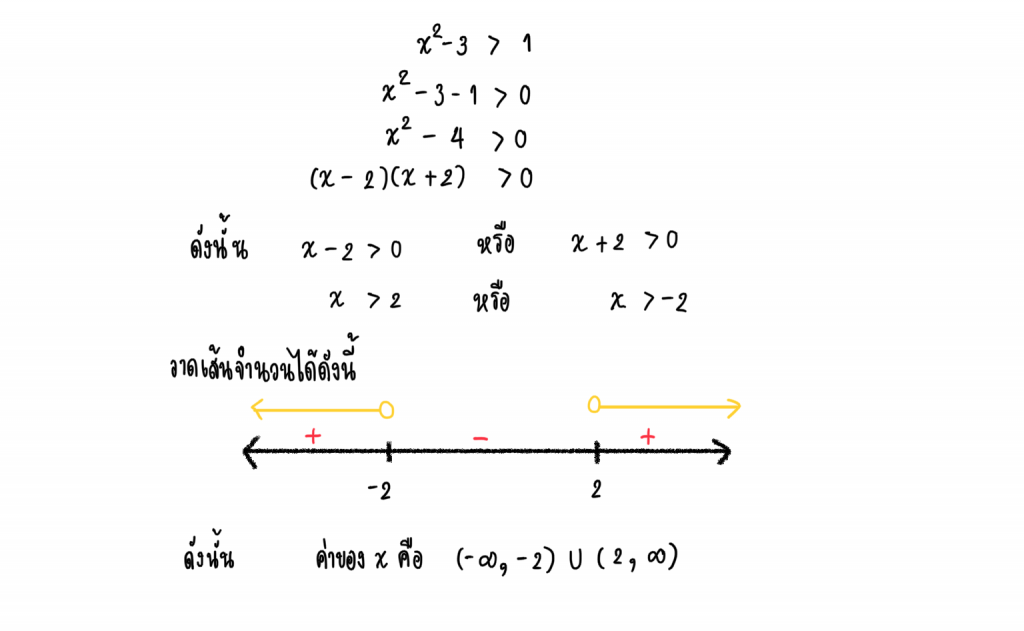
กรณีที่มีสองวงเล็บที่มากกว่า 0

เราจะเห็นว่าเส้นจำนวนแบ่งออกเป็น 3 ช่วง ถ้าเจอแบบนี้ให้น้องๆ

1.)ทดเครื่องหมายบวกไว้ที่ช่องขวาสุด ช่องถัดไปเป็นลบสลับแบบนี้ไปเรื่อยๆ (เริ่มจากขวาเสมอ) 

2.)พิจารณาเครื่องหมายของอสมการ จะเห็นว่าเป็นเครื่องหมายมากกว่า ดังนั้น ต้องลากเส้นไปทางเครื่องหมายบวกดังรูป

กลับกันถ้าเป็นกรณีน้อยกว่าให้ลากเส้นไปทางเครื่องหมายลบ ดังรูปในข้อ 4

3.) นำค่า x ของทั้งสองช่วงมา ยูเนียนกัน 

3.) จงหาค่า x เมื่อ x² + 3x – 18 ≥ 0 พร้อมกับวาดเส้นจำนวน

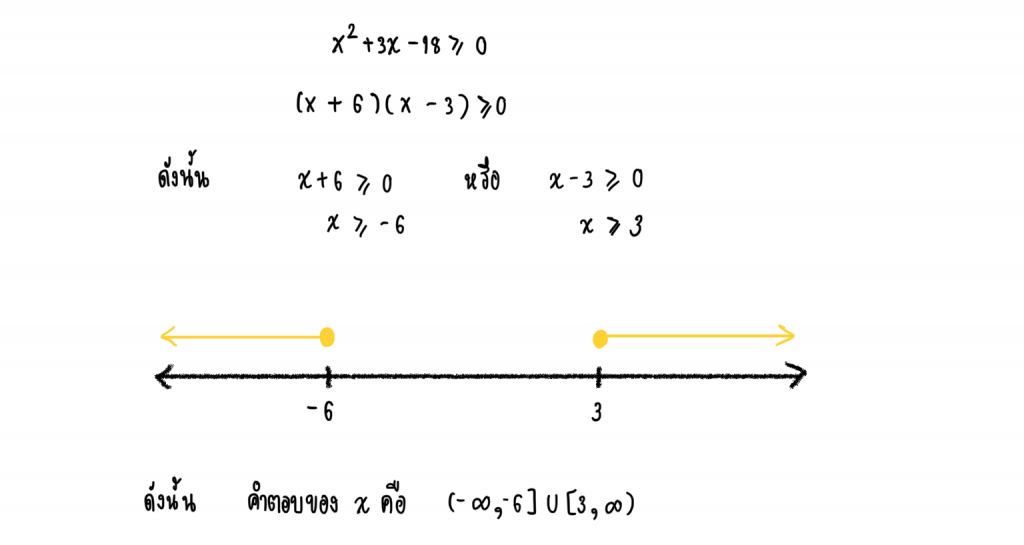
4.) (O-Net) กำหนดให้ I แทนเซตของจำนวนเต็ม และ A = {x : x ∈ I และ  2x² – 3x – 14 ≤ 0}

ผลรวมของสมาชิกในเซต A เท่ากับเท่าใด

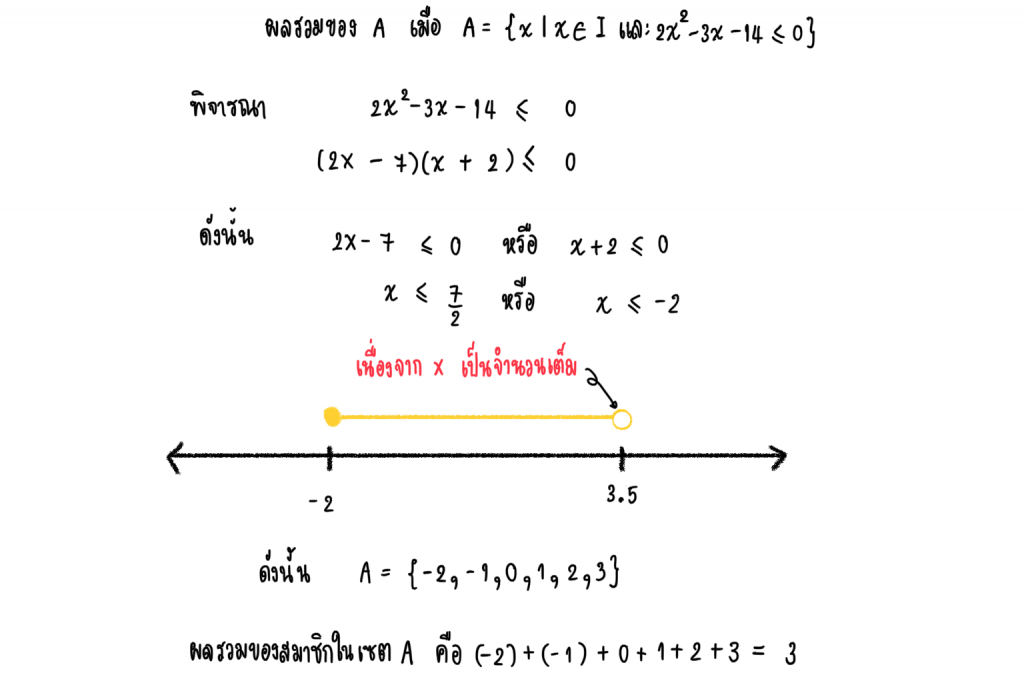
วีดิโอ อสมการ