รากที่ n ของจำนวนจริง และจำนวนจริงในรูปกรณฑ์

supanaree

คณิตศาสตร์, คณิตศาสตร์ เพิ่มเติม, ม.4

Add LINE friends for one click to find article.

รากที่ n ของจำนวนจริง

รากที่ n ของจำนวนจริง คือจำนวนจริงตัวหนึ่งยกกำลัง n แล้วเท่ากับ x เมื่อ n > 1 เราสามารถตรวจสอบรากที่ n ได้ง่ายๆ โดยนิยามดังนี้

นิยาม

ให้ x, y เป็นจำนวนจริง และ n เป็นจำนวนเต็มที่มากกว่า 1 เราจะบอกว่า y เป็นรากที่ n ของ x ก็ต่อเมื่อ $รากที่ n ของจำนวนจริง$

เช่น 5 เป็นรากที่ 3 ของ 125 หรือไม่

จากที่เรารู้ว่า 5×5×5 = 125 ดังนั้น เราจึงสรุปได้ว่า 5 เป็นรากที่ 3 ของ 125 หรือสามารถพูดได้อีกแบบคือ รากที่ 3 ของ 125 คือ 5 เขียนให้สั้นลงได้เป็น $\sqrt[3]{125}=5$ นั่นเอง

ในกรณีที่ x = 0 จะได้ว่า $\sqrt[n]{x}$ = 0

แต่ถ้า x > 0 จะได้ว่า n จะเป็นเลขคู่หรือคี่ก็ได้

**เมื่อ n เป็นจำนวนเต็มคู่ จะได้ว่า รากที่ n ของ x เป็นได้ทั้งจำนวนบวกและจำนวนลบ

เช่น -2, 2 เป็นรากที่ 4 ของ 16 เพราะ $รากที่ n ของจำนวนจริง$ และ $รากที่ n ของจำนวนจริง$

ในกรณีที่ x < 0 ในระบบจำนวนจริง n ควรจะเป็นเลขคี่

สมมติว่า n เป็นเลขคู่

$\sqrt[4]{-16}$ จะเห็นว่าไม่มีจำนวนจริงใดยกกำลัง 4 แล้วได้ -16 เพราะปกติแล้วยกกำลังคู่ต้องได้จำนวนบวก ดังนั้นจึงไม่มีคำตอบในระบบจำนวนจริง (แต่มีคำตอบในจำนวนเชิงซ้อน ซึ่งน้องๆจะได้เรียนในบทจำนวนเชิงซ้อน)

สมมติว่า n เป็นเลขคี่

$\sqrt[3]{-125}$ = -5 เพราะ (-5)×(-5)×(-5) = (-5)³ = -125

จำนวนจริงในรูปกรณฑ์

กรณฑ์ หรือค่าหลักของราก มีนิยามดังนี้

นิยาม

ให้ x, y เป็นจำนวนจริง และ n เป็นจำนวนเต็มที่มากกว่า 1 จะบอกว่า y เป็นค่าหลักของรากที่ n ของ x ก็ต่อเมื่อ

y เป็นรากที่ n ของ x
xy ≥ 0

จากนิยามจะเห็นว่า ถ้า y จะเป็นค่าหลักของรากที่ n ของ x ได้ จะได้ต้องมีคูณสมบัติครบทั้งสองข้อ มีข้อใดข้อหนึ่งไม่ได้

และเราจะเขียน $\sqrt[n]{x}$ แทนค่าหลักของรากที่ n ของ x อ่านได้อีกอย่างว่า กรณฑ์ที่ n ของ x

ตัวอย่าง

-3 เป็นกรณฑ์ที่ 3 ของ -27 เพราะว่า

-3 เป็นรากที่ 3 ของ 3 (เนื่องจาก $รากที่ n ของจำนวนจริง$ )
(-27)(-3) = 81 ≥ 0

-2 เป็นรากที่ 4 ของ 16 แต่ -2 นั้นไม่เป็นกรณฑ์ที่ 4 ของ 16 เพราะว่า (-2)(16) = -32 < 0

สมบัติที่ควรรู้

ให้ a, b เป็นจำนวนจริง และ m, n เป็นจำนวนเต็มที่มากกว่า 1

$จำนวนจริงในรูปกรณฑ์$
$\sqrt[n]{1}=1$
$\sqrt[n]{0}=0$
$(\sqrt[n]{a})^n=a$
$\sqrt[n]{ab}=\sqrt[n]{a}\times \sqrt[n]{b}$
$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}},b\neq 0$
$\sqrt[n]{a^{n}}$ = a เมื่อ n เป็นจำนวนเต็มคี่ เช่น $\sqrt[3]{(-3)^3} = -3$ , $\sqrt[5]{2^{5}}=2$
$\sqrt[n]{a^{n}}$ = $\left | a \right |$ เมื่อ n เป็นจำนวนเต็มคู่ เช่น $\sqrt[4]{2^{4}}= \left | 2 \right |=2$ , $\sqrt[4]{(-3)^4}=\left | -3 \right |=3$

สูตรลัดในการหารากที่ 2

$รากที่ n ของจำนวนจริง$

ตัวอย่าง

1.) $รากที่ n ของจำนวนจริง$

2.) $\sqrt[3]{4\sqrt[3]{4\sqrt[3]{4...}}}= \sqrt[3-1]{4}=\sqrt[2]{4}=2$

การหาผลบวก และผลต่างของจำนวนจริงในรูปกรณฑ์

วิธีการหาคือ

อันดับของกรณฑ์ต้องเหมือนกัน
เลขข้างในต้องเหมือนกันด้วย โดยอาจจะทำให้เป็นจำนวนเฉพาะหรืออาจจะทำให้เป็นจำนวนที่ต่ำที่สุด

ตัวอย่าง

1.) $3\sqrt{8}-\sqrt{2}+\sqrt{32}$

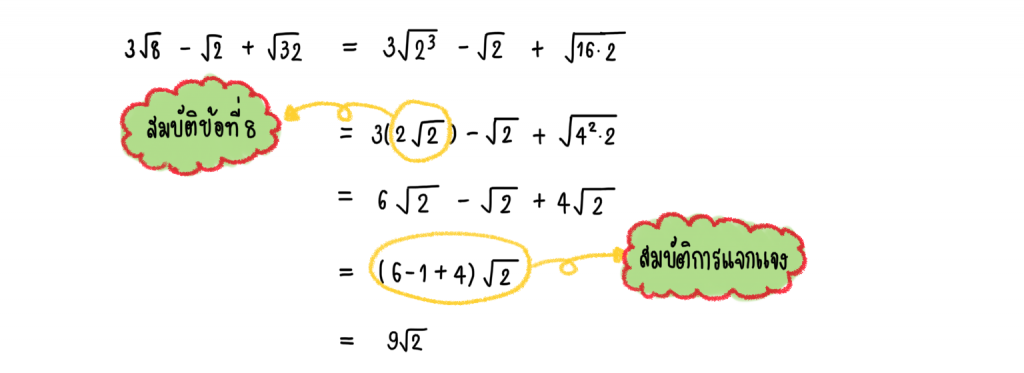
การหาผลคูณและผลหารของจำนวนจริงในรูปกรณฑ์

หลักการก็คือ

อันดับของกรณฑ์ต้องเหมือนกัน
ถ้าอันดับของกรณฑ์ไม่เหมือนกันจะต้องทำให้อันดับเหมือนกันก่อน โดยใช้สมบัติ

ตัวอย่าง

จะเขียน $\sqrt[3]{8}\sqrt{6}$ ให้อยู่ในรูปอย่างง่าย

วิดีโอ รากที่ n ของจำนวนจริง และจำนวนจริงในรูปกรณฑ์

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

เรียนรู้และประเมินคุณค่าบทประพันธ์ อิศรญาณภาษิต

หลังจากครั้งที่แล้ว ที่เราได้เรียนรู้ประวัติความเป็นมา ลักษณะคำประพันธ์ และตัวบทที่สำคัญในเรื่องกันแล้ว ครั้งนี้เรื่องที่น้อง ๆ จะได้เรียนรู้ต่อไปก็คือคุณค่าที่อยู่ใน อิศรญาณภาษิต นั่นเองค่ะ อย่างที่รู้กันว่าวรรณคดีเรื่องนี้อัดแน่นไปด้วยคำสอนและข้อคิดเตือนใจต่าง ๆ มากมาย เพราะงั้นเราไปเรียนรู้กันให้ลึกขึ้นดีกว่านะคะว่าคุณค่าในเรื่องนี้จะมีด้านใดบ้าง ไปดูกันเลยค่ะ คุณค่าในเรื่องอิศรญาณภาษิต คุณค่าด้านเนื้อหา อิศรญาณภาษิต มีเนื้อหาที่เป็นคำสอน ข้อคิดเตือนใจ เพื่อให้คนในสังคมได้ตระหนักถึงการกระทำของตน ว่าทำอย่างไรจึงจะอยู่ร่วมกับผู้อื่นอย่างเป็นปกติสุขได้

ตัวผกผันของความสัมพันธ์

ตัวผกผันของความสัมพันธ์ ตัวผกผันของความสัมพันธ์ r คือความสัมพันธ์ใหม่ที่เกิดจากการสลับตำแหน่งของสมาชิกตัวหน้ากับสมาชิกตัวหลังของคู่อันดับทุกคู่ในความสัมพันธ์ r เขียนแทนด้วย ซึ่ง = {(y, x) : (x, y ) ∈ r} เช่น r = {(1, 2), (3, 4), (5,

ฟังก์ชันประกอบ

ฟังก์ชันประกอบ ฟังก์ชันประกอบ คือฟังก์ชันที่เกิดจากการหาค่าฟังก์ชันที่ส่งจากเซต A ไปเซต C โดยที่ f คือฟังก์ชันที่ส่งจาก A ไปยัง B และ g เป็นฟังก์ชันที่ส่งจาก B ไปยัง C เราเรียกฟังก์ชันที่ส่งจาก A ไป C นี้ว่า gof จากรูป

กาพย์ห่อโคลงประพาสธารทองแดง ที่มาของวรรณคดีเชิงสารคดี

กาพย์ห่อโคลงประพาสธารทองแดง มีมาตั้งแต่สมัยอยุธยา เป็นวรรณคดีที่สำคัญในฐานะสารคดี เหตุใดจึงเป็นเช่นนั้น บทเรียนในวันนี้จะพาน้อง ๆ ไปหาคำตอบของวรรณคดีเรื่องดังกล่าวว่ามีประวัติความเป็นมาอย่างไร ใครเป็นผู้แต่ง พร้อมเรียนรู้ความหมายของกาพย์ห่อโคลงและเนื้อเรื่องโดยสรุปของเรื่องด้วย ไปเรียนรู้เรื่องนี้พร้อมกันเลยค่ะ ความเป็นมาของ กาพย์ห่อโคลงประพาสธารทองแดง กาพย์ห่อโคลงประพาสธารทองแดงเป็นบทชมธรรมชาติที่แต่งเพื่อความเพลิดเพลินระหว่างการเดินทางของกระบวนเสด็จทางสถลมารคจากท่าเจ้าสนุกถึงธารทองแดง ซึ่งธารทองแดงในที่นี้ เป็นชื่อลำน้ำที่เขาพระพุทธบาท ซึ่งเป็นบริเวณที่ตั้งของพระตำหนักธารเกษมที่มีมาตั้งแต่สมัยสมเด็จพระเจ้าปราสาททอง โดยเจ้าฟ้าธรรมธิเบศรทรงพระนิพนธ์วรรณคดีเรื่องนี้ขึ้นเมื่อครั้งตามเสด็จสมเด็จพระเจ้าอยู่หัวบรมโกศไปนมัสการพระพุทธบาท ที่จังหวัดสระบุรี ประวัติเจ้าฟ้าธรรมธิเบศร เจ้าฟ้าธรรมธิเบศร

แบบฝึกหัดการให้เหตุผล

แบบฝึกหัดการให้เหตุผล แบบฝึกหัดการให้เหตุผล ประกอบไปด้วยการให้เหตุผลแบบอุปนัยและการให้เหตุผลแบบนิรนัย ซึ่งแบบฝึกหัดนี้จะช่วยให้น้องๆได้ฝึกฝนการทำโจทย์จนน้องๆเชี่ยวชาญและส่งผลให้น้องๆทำข้อสอบได้แบบไม่ผิดพลาด ถ้าเรารู้เฉยๆเราอาจจะทำข้อสอบได้แต่การที่เราฝึกทำโจทย์ด้วยจะทำให้เราทำข้อสอบได้แน่นอนค่ะ แบบฝึกหัดเพิ่มเติมและข้อสอบ O-Net ตัวอย่างต่อไปนี้เป็นข้อสอบ O-Net ของปีก่อนๆ 1.) พิจารณาการอ้างเหตุผลต่อไปนี้ ก. เหตุ 1. ถ้าฝนไม่ตกแล้วเดชาไปโรงเรียน 2. ฝนตก ผล

ศึกษาประวัติความเป็นมาและเรื่องย่อของเรื่องราชาธิราช ตอน สมิงพระรามอาสา

ราชาธิราช เป็นวรรณคดีประเภท พงศาวดาร ที่มีการแปลมาจากพงศาวดารมอญ น้อง ๆ หลายคนคงจะทราบกันดีอยู่แล้วว่าพงศาวดารก็คือเรื่องราวหรือเหตุการณ์ที่เกี่ยวกับประเทศชาติหรือพระมหากษัตริย์ แต่ทราบกันหรือไม่คะว่าทำไมในแบบเรียนภาษาไทยของเรานั้นถึงต้องเรียนเรื่องราชาธิราช ที่เป็นพงศาวดารมอญด้วย วันนี้เราจะพาน้อง ๆ ทุกคนไปเรียนรู้ประวัติความเป็นมาของเรื่องราชาธิราชรวมไปถึงเรื่องย่อ ซึ่งในบทที่เราจะเรียนนี้คือตอน สมิงพระรามอาสา เรื่องราวจะเป็นอย่างไรบ้าง ไปศึกษาเรื่องนี้พร้อม ๆ กันเลยค่ะ ราชาธิราช ประวัติความเป็นมา ราชาธิราชเป็นวรรณคดีร้อยแก้วที่พระบาทสมเด็จพระพุทธยอดฟ้าจุฬาโลกมหาราชโปรดเกล้าฯ

รากที่ n ของจำนวนจริง และจำนวนจริงในรูปกรณฑ์

สารบัญ

รากที่ n ของจำนวนจริง

จำนวนจริงในรูปกรณฑ์

สมบัติที่ควรรู้

การหาผลบวก และผลต่างของจำนวนจริงในรูปกรณฑ์

การหาผลคูณและผลหารของจำนวนจริงในรูปกรณฑ์

วิดีโอ รากที่ n ของจำนวนจริง และจำนวนจริงในรูปกรณฑ์

แค่ 10 นาที ก็เข้าใจได้

แนะนำ

แชร์

เรียนรู้และประเมินคุณค่าบทประพันธ์ อิศรญาณภาษิต

ตัวผกผันของความสัมพันธ์

ฟังก์ชันประกอบ

กาพย์ห่อโคลงประพาสธารทองแดง ที่มาของวรรณคดีเชิงสารคดี

แบบฝึกหัดการให้เหตุผล

ศึกษาประวัติความเป็นมาและเรื่องย่อของเรื่องราชาธิราช ตอน สมิงพระรามอาสา

NockAcademy

ติดต่อ

เกี่ยวกับเรา

ความช่วยเหลือ

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1