ความเท่ากันทุกประการของรูปเรขาคณิตเกิดจากการสะท้อน การเลื่อนขนาน และการหมุน ซึ่งเป็นตัวอย่างของการเคลื่อนที่รูปเรขาคณิตซึ่งเป็นการแปลงตำแหน่งของรูปเรขาคณิตบนระนาบโดยที่ระยะระหว่างจุดสองจุดใด ๆของรูปนั้นไม่เปลี่ยนแปลง หมายความถึงว่า รูปร่างและขนาดของรูปเรขาคณิตที่เคลื่อนที่นั้นไม่เปลี่ยนแปลง
ความเท่ากันทุกประการของรูปเรขาคณิต
พิจารณารูปต่อไปนี้
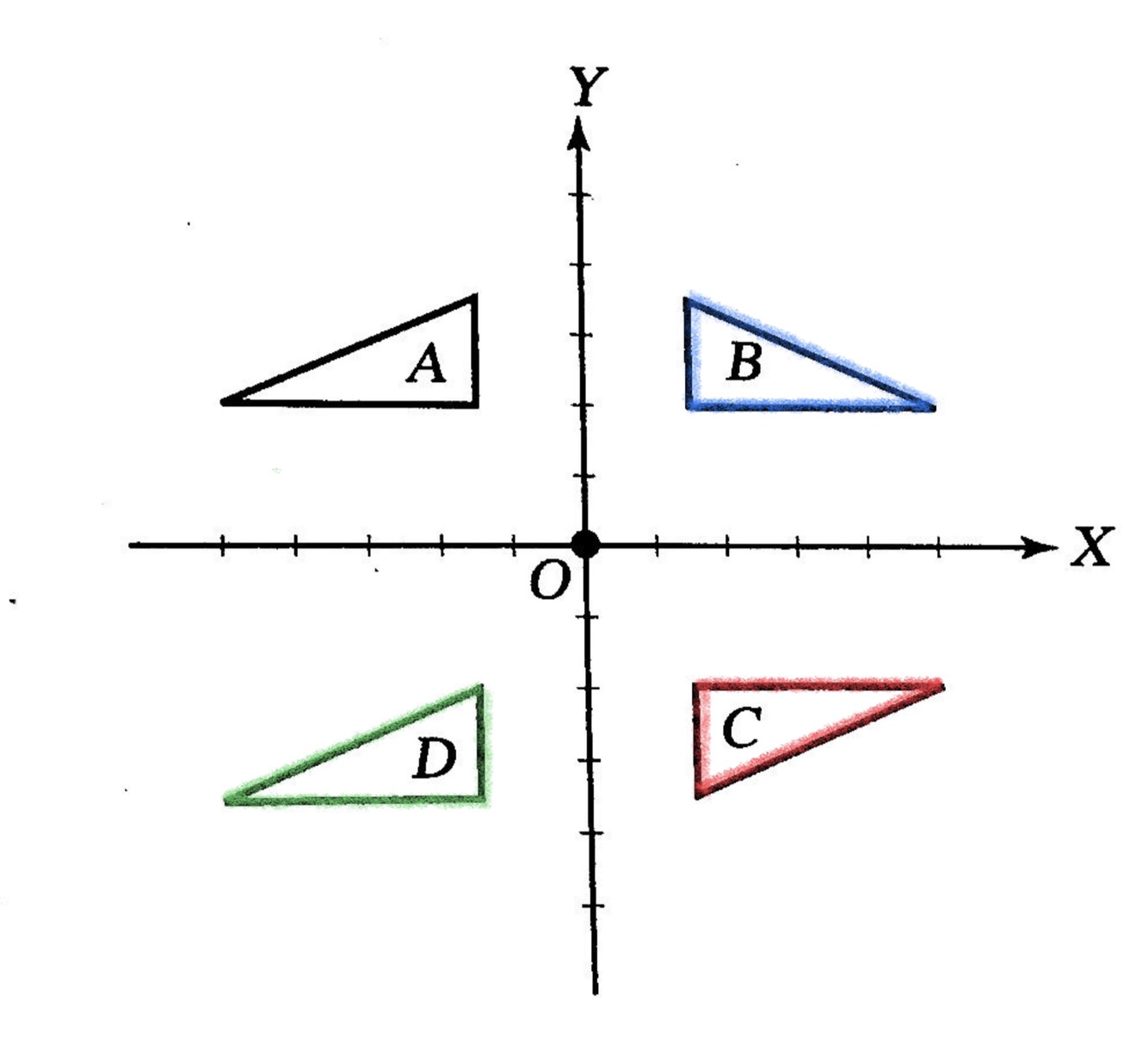
ถ้าเรากำหนดให้ A เป็นรูปต้นแบบ และ A เกิดการแปลงไปเป็นรูป B C และ D ซึ่งเกิดจากการ “เคลื่อนที่” รูป A ดังนี้
รูป B เกิดจากการสะท้อนที่แกน Y
รูป D เกิดจากการเลื่อนขนานไปตามแกน Y
รูป C เกิดจากการหมุนรูป A ไป 180 °รอบจุด O
การเคลื่อนที่รูปเรขาคณิตจากการแปลงดังกล่าวข้างต้น เป็นตัวอย่างหนึ่งของการเปลี่ยนตำแหน่งของรูปเรขาคณิตบนระนาบ โดยที่ระยะระหว่างจุดสองจุดใด ๆ ของรูปนั้นไม่เปลี่ยนแปลง
แสดงว่ารูปร่างและขนาดของรูปเรขาคณิตที่เคลื่อนที่นั้นไม่เปลี่ยนแปลง และถ้าเราเคลื่อนรูป A B C และ D มาทับกัน รูปทั้งหมดก็สามารถทับกันได้สนิท เราถือว่ารูปทั้งหมดนั้นเท่ากันทุกประการ
บทนิยาม “รูปเรขาคณิตสองรูปเท่ากันทุกประการก็ต่อเมื่อเคลื่อนที่รูปหนึ่งไปทับอีกรูปหนึ่งได้สนิท”

การตรวจสอบว่ารูปเรขาคณิตสองรูปใดเท่ากันทุกประการหรือไม่อาจทำได้โดยใช้กระดาษลอกลายลอกรูปหนึ่งแล้วยกไปทับอีกรูปหนึ่งถ้าทับกันได้สนิทแสดงว่ารูปเรขาคณิตเท่ากันทุกประการ
ความเท่ากันทุกประการของส่วนของเส้นตรง
ส่วนของเส้นตรงสองเส้นเท่ากันทุกประการก็ต่อเมื่อส่วนของเส้นตรงทั้งสองนั้นยาวเท่ากัน
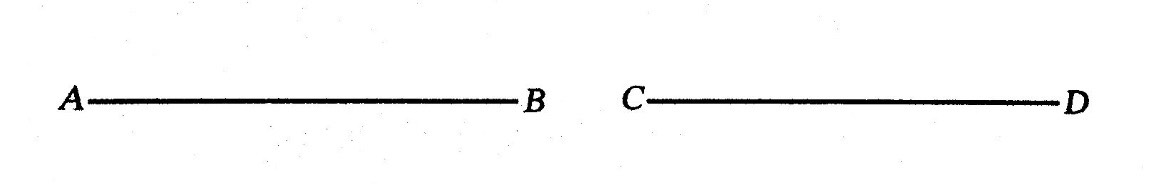
จากรูป AB เท่ากันทุกประการกับ CD แต่เวลาเขียนเป็นสัญลักษณ์ไม่นิยมเขียนว่า AB = CD จะเขียนเพียง AB = CD เท่านั้น
ความเท่ากันทุกประการของมุม
มุมสองมุมเท่ากันทุกประการก็ต่อเมื่อมุมทั้งสองมุมนั้นมีขนาดเท่ากัน
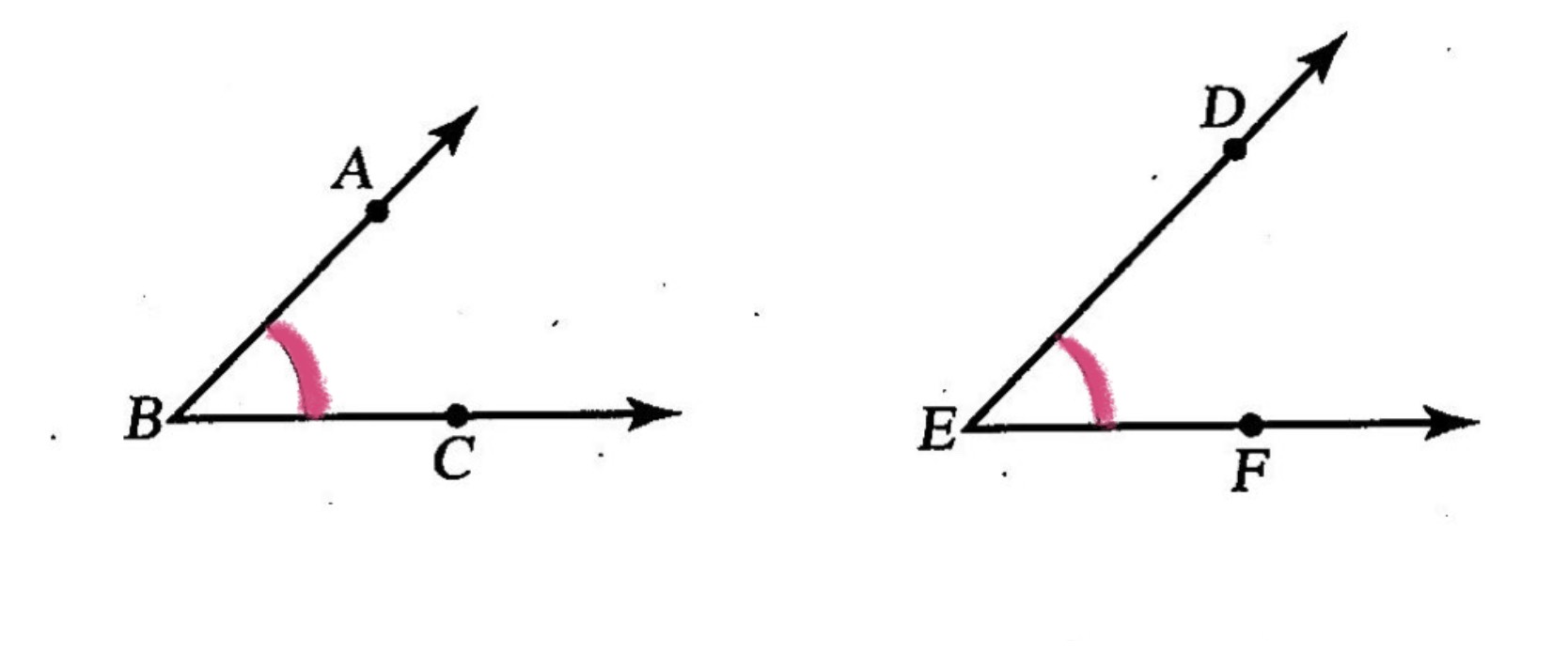
จากรูป ถ้า <ABC = <DEF แล้ว <ABC = <DEF และการเขียนสัญลักษณ์แทนการเท่ากันทุกประการของมุมจะเขียนเพียง <ABC = <DEF เท่านั้น
ข้อสังเกต
- เส้นตรงสองเส้นตัดกันจะเกิดมุมที่เท่ากันทุกประการ 2 คู่เรียกว่า “มุมตรงข้าม”
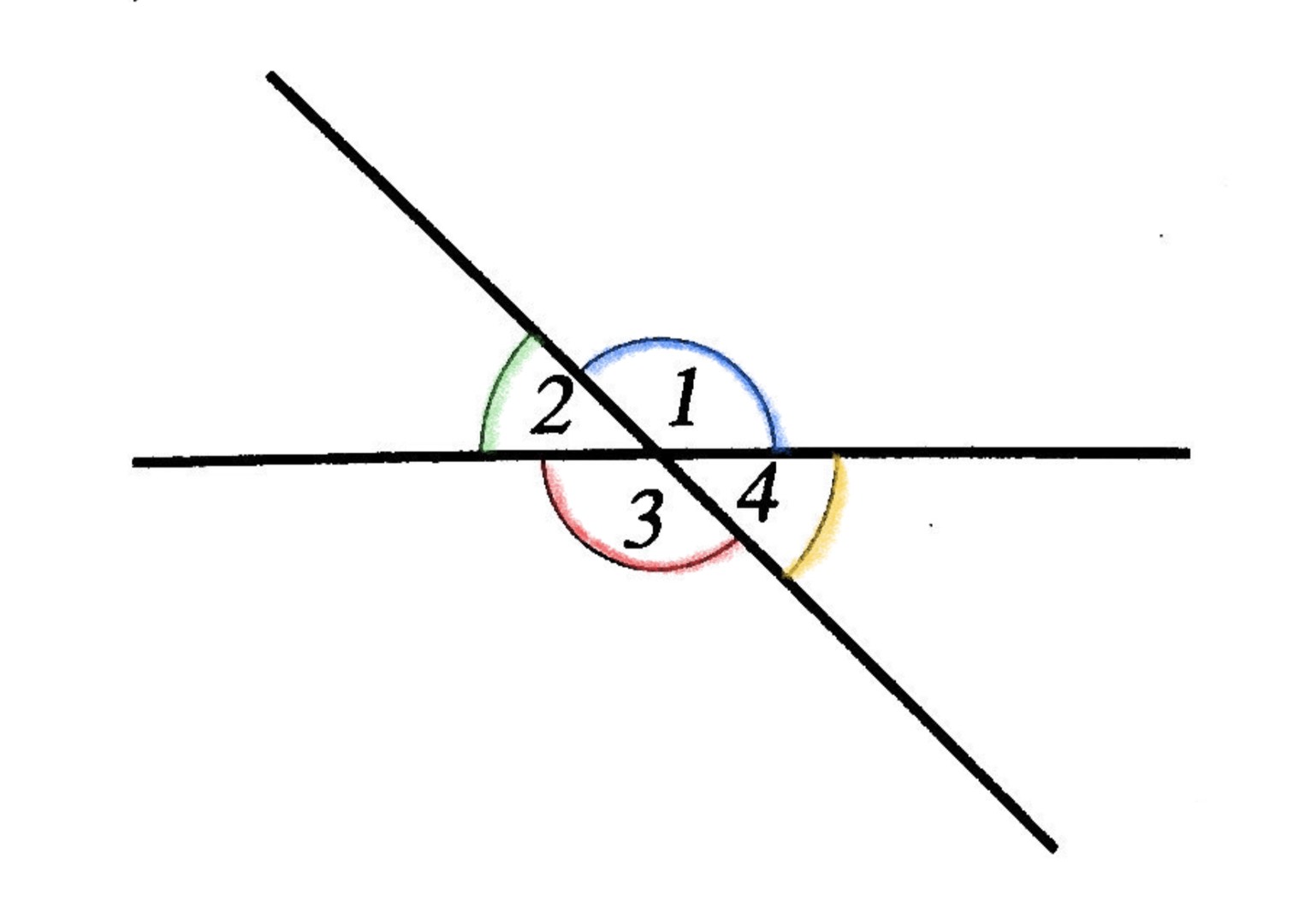
- ถ้ากำหนดให้รูป A = B และรูป B = C แล้วจะได้ว่ารูป A = รูป C
- รูปสี่เหลี่ยมผืนผ้าที่มีพื้นที่เท่ากัน อาจจะไม่เท่ากันทุกประการ เช่น รูปทั้งสองมี พื้นที่ 18 ตารางหน่วย รูปแรกอาจจะมีขนาด 2×9 ตารางหน่วยและรูปที่ 2 อาจจะมีขนาด 3 X 6 ตารางหน่วยเป็นต้น
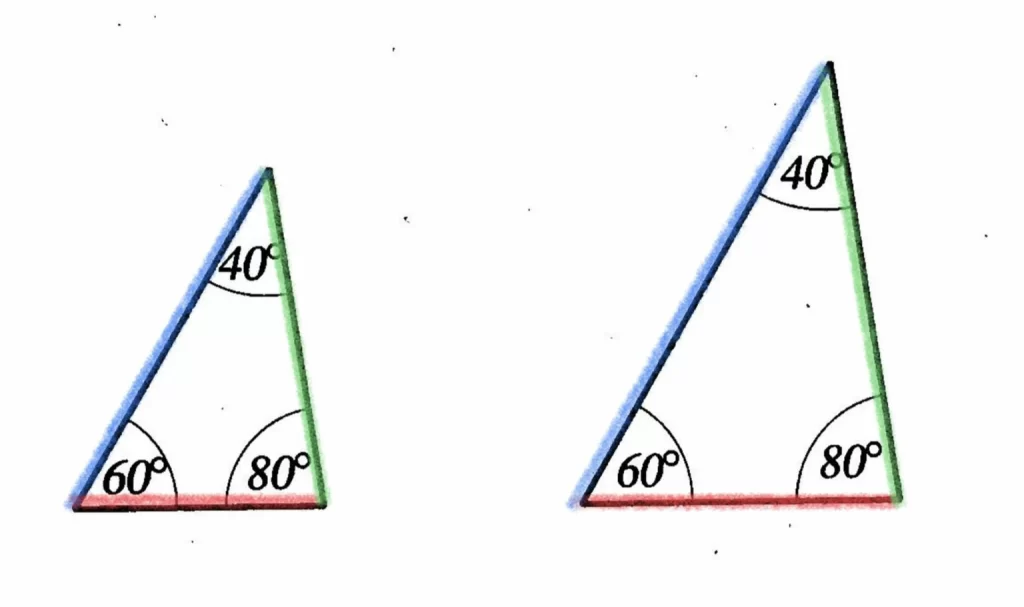
- รูปสามเหลี่ยมสองรูปที่มีมุมเท่ากัน 3 คู่อาจจะไม่เท่ากันทุกประการ เช่น
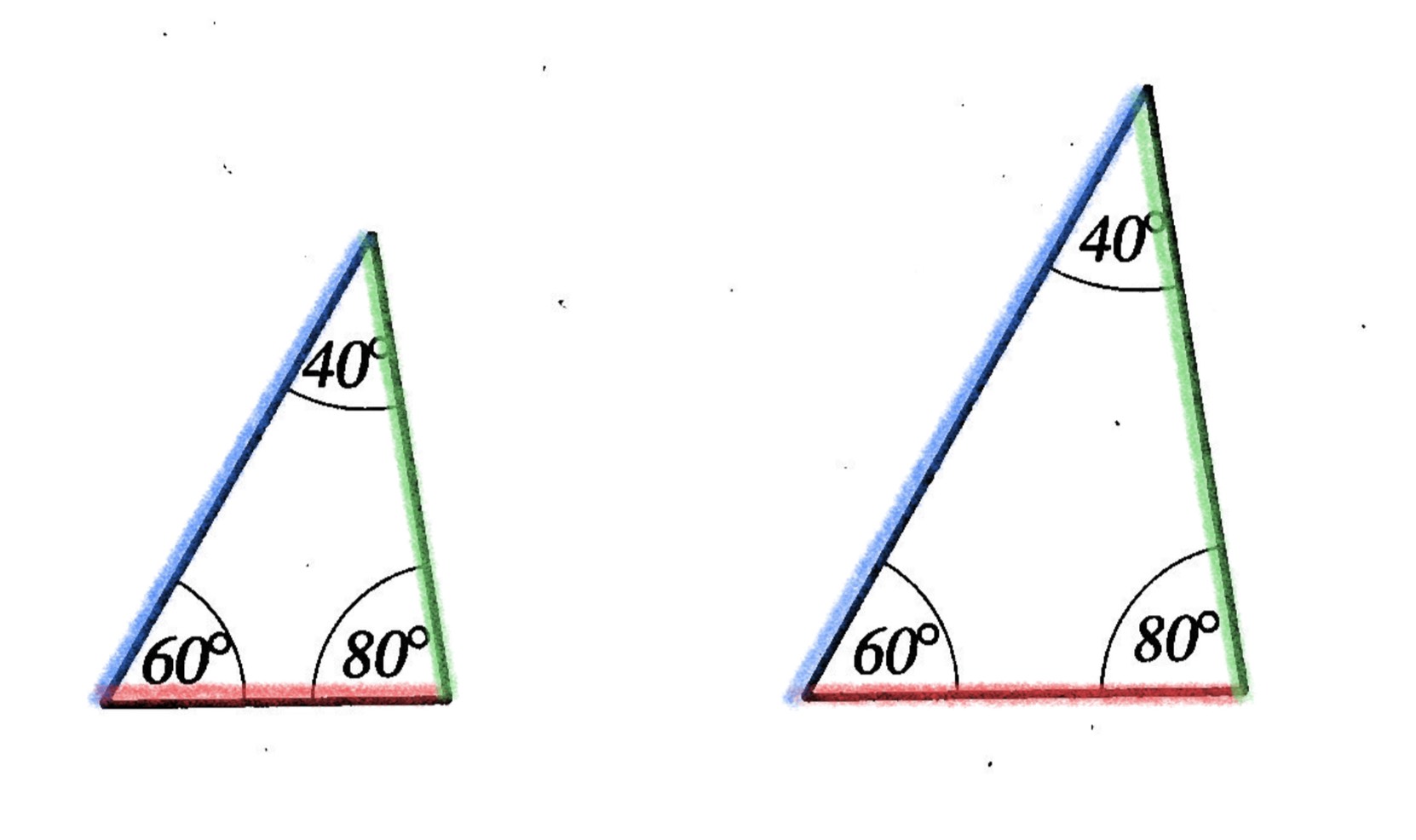
- วงกลม 2 วงที่มีรัศมียาวเท่ากันจะเท่ากันทุกประการ
- รังสี 2 เส้นใด ๆ จะเท่ากันทุกประการ
- รูปสี่เหลี่ยมจัตุรัส 2 รูปที่มีพื้นที่เท่ากันจะเท่ากันทุกประการ