เรนจ์ของความสัมพันธ์

เรนจ์ของความสัมพันธ์ r คือ สมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย

กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหลัง

เช่น = {(2, 2), (3, 5), (8, 10)}

จะได้ว่า  = {2, 5, 10}

กรณีที่ r เขียนในรูปแบบที่บอกเงื่อนไข เราอาจจะสามารถนำมาเขียนแบบแจกแจงสมาชิกได้

เช่น ให้ A = {1, 2, 3} และ = {(x, y) ∈ A × A : y = 2x}

x = 1 ; y = 2(1) = 2

x = 2 ; y = 2(2) = 4

x = 3 ; y = 2(3) = 6

ได้คู่อันดับ ดังนี้ (1, 2), (2, 4), (3, 6) เนื่องจาก (x, y) ต้องเป็นสมาชิกใน A × A

และจาก (1, 2) ∈ A × A

(2, 4) ∉ A × A

(3, 6) ∉ A × A

ดังนั้น สามารถเขียน r ในรูปแจกแจงสมาชิกได้ดังนี้  = {(1, 2)} จากเรนจ์ของความสัมพันธ์คือสมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r

สรุปได้ว่า = {2}

แต่บางกรณีเราไม่สามารถแจกแจงสมาชิกได้ เช่น ให้ x, y เป็นจำนวนจริงใดๆ และ = {(x, y) : y = }

พิจารณากราฟของสมการ y =

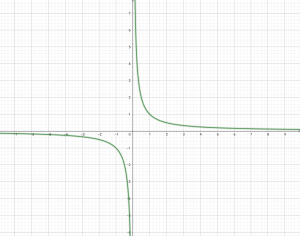
จะเห็นว่ากราฟของ y = ไม่ตัดแกน x นั่นคือ y ≠ 0

และจาก เรนจ์ของความสัมพันธ์คือ สมาชิกตัวหลังของคู่อันดับ ซึ่งก็คือ y นั่นเอง 

หรืออาจจะสังเกตจากสมการก็ได้ เนื่องจาก x เป็น 0 ไม่ได้ นั่นก็แปลว่ายังไง y ก็ไม่เป็น 0 แน่นอน

ดังนั้น = {y : y  เป็นจำนวนจริง และ y ≠ 0}

ตัวอย่างการหาเรนจ์ของความสัมพันธ์

1.) ให้ A = {1, 2, 3} และ r = {(x, y) : y = 2x , x ∈ A}

จาก x เป็นสมาชิกใน A 

x = 1 ; y = 2(1) = 2

x = 2 ; y = 4

x = 3 ; y = 6

r = {(1, 2), (2, 4), (3, 6)}

ดังนั้น = {2, 4, 6}

2.) ให้ r = {(x, y) ∈ : y = x²}

เงื่อนไขของ (x, y) ∈  

พิจารณากราฟ y = x²

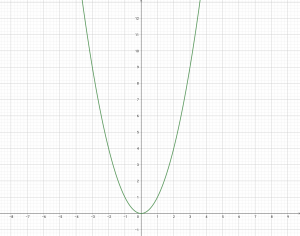
จากเรนจ์คือสมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r นั่นก็คือ y นั่นเอง

และจากกราฟจะเห็นว่า ค่า y มีค่าตั้งแต่ 0 ทำให้ได้ว่า y เป็นจำนวนจริงที่มากกว่าหรือเท่ากับ 0 

หรือจะสังเกตจากสมการเลยก็ได้ จาก y = x²  จากที่เรารู้อยู่แล้วว่า จำนวนจริงยกกำลังสองยังไงก็ไม่เป็นลบแน่นอน เราเลยรู้ว่า y ยังไงก็ต้องเป็นบวกหรือ 0 

ดังนั้น = {y : y เป็นจำนวนจริง และ y ≥ 0}

3.) ให้ r = {(x, y) : y = } และ x, y เป็นจำนวนจริงใดๆ

พิจารณากราฟของ y = จะได้

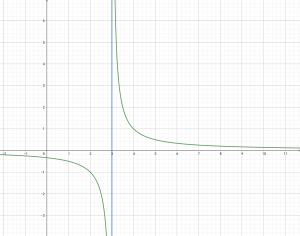
จากเรนจ์คือสมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r นั่นก็คือ y นั่นเอง

และจากกราฟจะเห็นว่า กราฟไม่ตัดแกน x เลย (จุดที่กราฟตัดแกน x คือจุดที่ y = 0) นั่นคือ y เป็นอะไรก็ได้แต่ไม่มีทางเป็น 0 

หรือจะสังเกตจากสมการ y = จากที่รู้ว่า x นั้นเป็น 3 ไม่ได้ (เพราะจะทำให้ y หาค่าไม่ได้) แต่เมื่อแทน x เป็นจำนวนจริงอื่น ยังไง y ก็ไม่มีทางเป็น 0 เพราะตัวเศษเป็นค่าคงที่

ดังนั้น = {y : y เป็นจำนวนจริง และ y ≠ 0}

4.) ให้ r = {(x, y) : y = } และ x, y เป็นจำนวนจริงใดๆ

พิจารณากราฟของสมการ y =

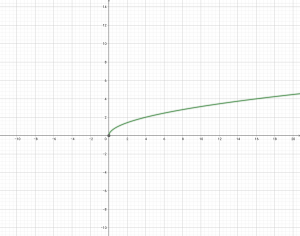
จากเรนจ์คือสมาชิกตัวหลังของคู่อันดับในความสัมพันธ์ r นั่นก็คือ y นั่นเอง

และจากกราฟจะเห็นว่า y ไม่เป็นลบเลย นั่นคือ y มากกว่าหรือเท่ากับ 0

หรือจะสังเกตจากสมการก็ได้ จากสมการ y = จากที่เรารู้ว่าโดเมนหรือ x เป็นลบ ไม่ได้ นั่นคือ x มากกว่าหรือเท่ากับ 0 ทำให้ได้ว่า y ไม่มีทางเป็นลบเหมือนกัน

ดังนั้น = {y : y ∈ R และ y ≥ 0}

วิดีโอ เรนจ์ของความสัมพันธ์

https://youtu.be/dHYXyKemluc

เนื้อหาที่ควรรู้และเกี่ยวข้องกับเรนจ์ของความสัมพันธ์

1. กราฟของความสัมพันธ์
2. โดเมนของความสัมพันธ์