สัจนิรันดร์ คือรูปแบบของประพจน์ที่มีค่าความจริงเป็นจริงเสมอ
วิธีการพิสูจน์การเป็นสัจนิรันดร์
การพิสูจน์ทำได้หลายวิธีไม่ว่าจะเป็น มองจากตารางค่าความจริง หรืออาจจะหาข้อขัดแย้งก็ได้
1) วิธีพิสูจน์จากตารางค่าความจริง
ถ้าเรามองจากตารางค่าความจริงประพจน์ที่เราพิจารณาจะต้องเป็น “จริงทุกกรณี” ถ้าเป็นเท็จแค่กรณีเดียวถือว่าไม่เป็นสัจนิรันดร์
เช่น พิจารณาประพจน์ (p→q)∨p ว่าเป็นสัจนิรันดร์หรือไม่
วิธีพิสูจน์ เราจะใช้วิธีสร้างตารางค่าความจริง ของประพจน์ (p→q)∨p
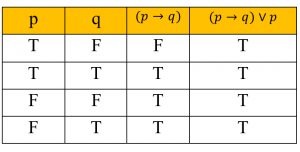
จากตารางจะเห็นว่าทุกกรณีมีค่าความจริงทั้งหมด ดังนั้นประพจน์ (p→q)∨p
เป็นสัจนิรันดร์
ลองมาดูตัวอย่างกรณีที่ไม่เป็นสัจนิรันดร์
พิจารณาประพจน์ (p∨q)→q ว่าเป็นสัจนิรันดร์หรือไม่
เราจะสร้างตารางค่าความจริง ดังนี้
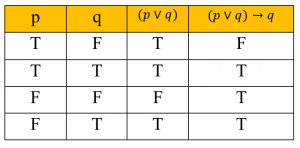
จากตารางจะได้ว่า ประพจน์ (p→q)∨p ไม่เป็นสัจนิรันดร์ เพราะว่ามีกรณีที่ทำให้ประพจน์มีค่าความจริงเป็นเท็จ
จากตัวอย่าง 2 ตัวอย่างนี้ จะเห็นว่าการใช้ตารางค่าความจริงจะทำให้เราเห็นภาพง่าย แต่ก็มีข้อเสียอยู่ คือ ในกรณีที่มีตัวแปร(p,q,r,s)มากกว่า 2 เราจะต้องหาทุกกรณีซึ่งจะทำให้เสียเวลามาก ดังนั้น การใช้ตารางค่าความจริงอาจจะไม่เหมาะกับโจทย์บางรูปแบบ
แต่ข้อดีของการใช้ตารางก็คือ สำหรับคนที่ไม่ค่อยแม่นจะทำให้เราเข้าใจและเห็นภาพได้ง่าย
2.) พิสูจน์ด้วยวิธีสมมติว่าเป็นเท็จ
ก็คือการสมมติว่าประพจน์มีค่าความจริงเป็นเท็จ จากนั้นเราก็จะพิจารณาว่า ประพจน์ดังกล่าว จะเป็นเท็จในกรณีไหนบ้าง ถ้าเกิดการขัดแย้งแสดงว่าประพจน์ดังกล่าวเป็นสัจนิรันดร์ แต่ถ้าไม่ขัดแย้งกันแสดงว่าประพจน์ดังกล่าวไม่เป็นสัจนิรันดร์ อ่านแล้วอาจจะงงๆ ลองมาดูตัวอย่างดีกว่าค่ะ
เช่น พิจารณาประพจน์ (p→q)∨p ว่าเป็นสัจนิรันดร์หรือไม่
วิธีพิสูจน์

3.) วิธียกตัวอย่างค้าน
วิธีจะเหมาะกับกรณีที่ไม่เป็นสัจนิรันดร์ เราจะยกตัวอย่างที่ทำให้ประพจน์ไม่เป็นสัจนิรันดร์
เช่น จงตรวจสอบว่า p→(p∧q) เป็นสัจนิรันดร์หรือไม่ ถ้าไม่จงยกตัวอย่าง
วิธีทำ กำหนดให้ p มีค่าความจริงเป็น จริง และ q มีค่าความจริงเป็นเท็จ
พิจารณาประพจน์ p→(p∧q)
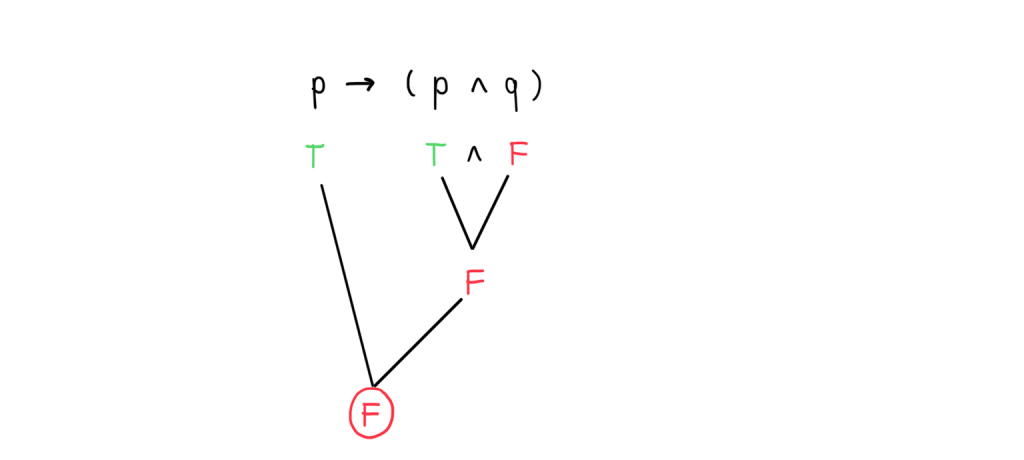
จะเห็นว่าเมื่อให้ p มีค่าความจริงเป็นจริง และ q มีค่าความจริงเป็นเท็จ เราจะได้ประพจน์ที่มีค่าความจริงเป็นเท็จ เมื่อมีกรณีที่เป็นเท็จอยู่ ทำให้ไม่เป็นสัจนิรันดร์
จำไว้ว่า สัจนิรันด์คือต้องเป็นจริงเสมอ ถ้ามีกรณีที่ทำให้เป็นเท็จ ประพจน์นั้นจะไม่เป็นสัจนิรันดร์ทันที!!
ตัวอย่าง
1.) จงพิสูจน์ว่าประพจน์ (p→q)↔(∼p∨q) เป็นสัจนิรันดร์
วิธีพิสูจน์ สร้างตารางค่าความจริงได้ดังนี้
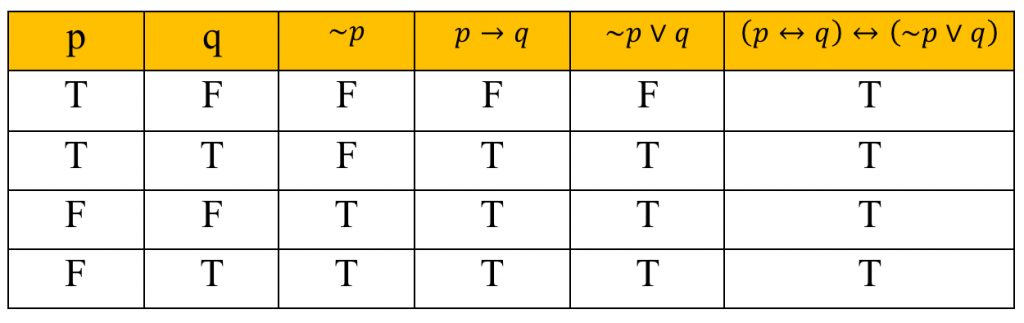
เนื่องจาก ค่าความจริงของประพจน์(p→q)↔(∼p∨q)มีความความจริงเป็นจริงทุกกรณี ดังนั้นประพจน์(p→q)↔(∼p∨q)เป็นสัจนิรันดร์
2.) จงแสดงว่าประพจน์ [(p→q)∧(q→r)]→(p→r) เป็นสัจนิรันดร์
วิธีทำ เราจะสมมติให้ ประพจน์[(p→q)∧(q→r)]→(p→r)มีค่าความจริงเป็นเท็จ
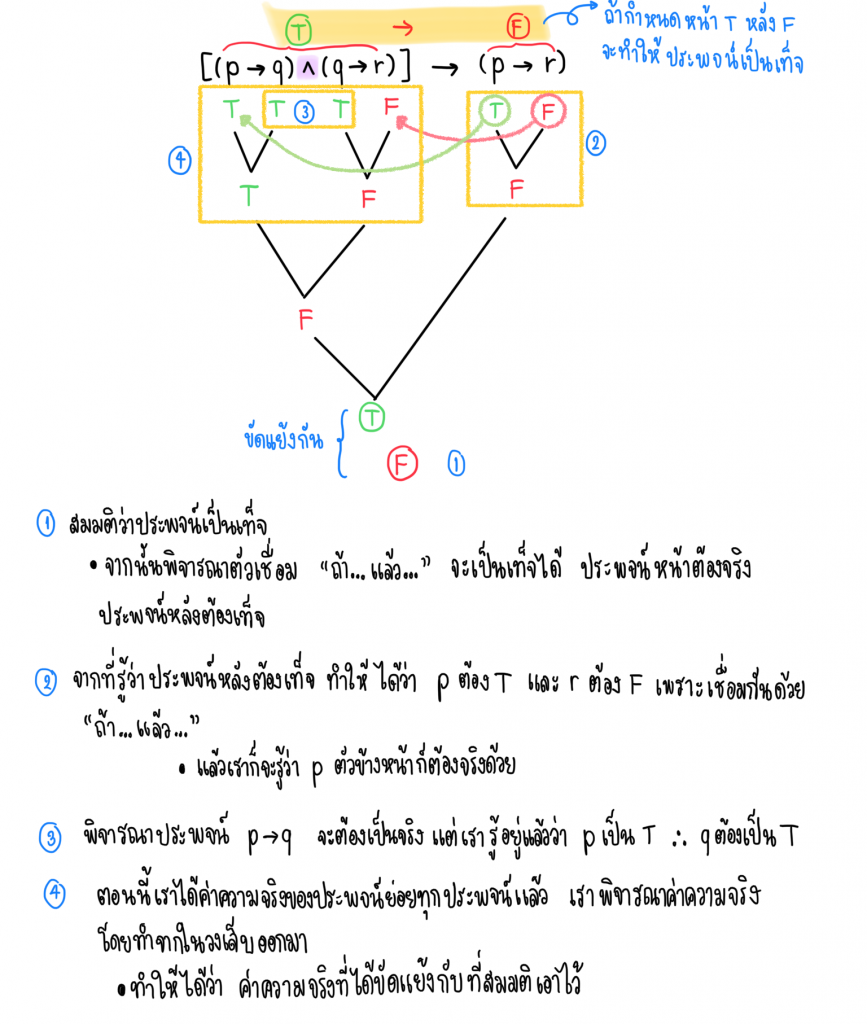
ดังนั้น [(p→q)∧(q→r)]→(p→r) เป็นสัจนิรันดร์
วิธีการเลือกใช้วิธีพิสูจน์ ให้ดูจากตัวเชื่อมระหว่างประพจน์2ประพจน์ ถ้าเป็น “→” และ “∨” มักจะใช้วิธีสมมติขัดแย้งได้ แต่ถ้าเป็นอย่างอื่นอาจจะต้องใช้วิธีการยกตัวอย่างกรณีที่ทำให้เป็นเท็จ หรือจำเป็นที่จะต้องทำตารางค่าความจริง
หลังจากศึกษาดูตัวอย่างแล้วน้องๆอาจจะยังเลือกไม่ค่อยได้ว่ากรณีไหนควรใช้วิธีแบบไหน แต่หากน้องๆหมั่นทำโจทย์จะทำให้น้องเชี่ยวชาญการใช้วิธีพิสูจน์มากขึ้น และจะทำให้น้องๆได้ทวนเรื่องค่าความจริงของประพจน์ไปด้วย
ไม่มีใครเข้าใจตั้งแต่ครั้งแรกที่เรียน ถ้าน้องเปิดใจให้วิชาคณิตศาสตร์และขยันทำโจทย์ คณิตศาสตร์ก็เป็นอีกวิชาที่สนุก สู้ๆนะคะ❤️❤️



















