การวัดความยาวส่วนโค้ง
การวัดความยาวส่วนโค้ง ในบทความนี้จะเป็นการวัดความยาวของวงกลม 1 หน่วย
วงกลมหนึ่งหน่วย คือวงกลมที่มีจุดศูนย์กลางที่จุดกำเนิด และมีรัศมียาว 1 หน่วย
จากสูตรของเส้นรอบวง คือ 2r ดังนั้นวงกลมหนึ่งหน่วย จะมีเส้นรอบวงยาว 2
และครึ่งวงกลมยาว
จุดปลายส่วนโค้ง
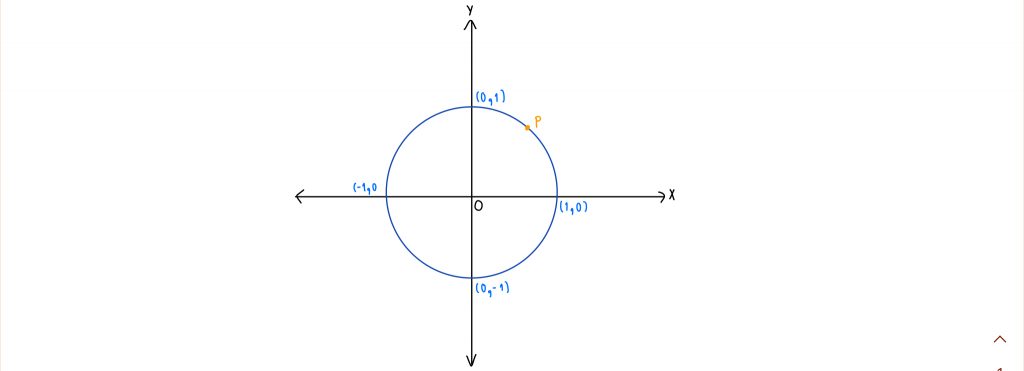
จากรูป จะได้ว่าจุด P เป็นจุดปลายส่วนโค้ง
จากที่เราได้ทำความรู้จักกับวงกลมหนึ่งหน่วยและจุดปลายส่วนโค้งแล้ว ต่อไปเราจะมาทำความเข้าใจเรื่องการวัดความยาวส่วนโค้งกันนะคะ
การวัดความยาวส่วนโค้ง ของวงกลมหนึ่งหน่วย
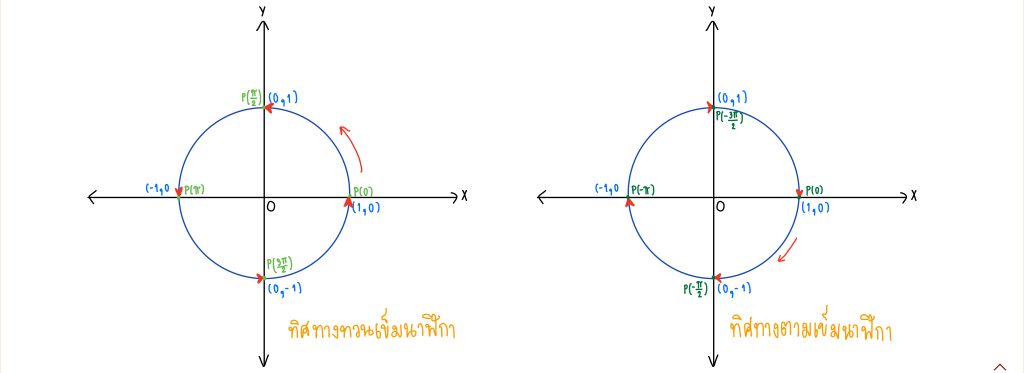
กำหนดให้ θ ∈ จะบอกว่า P(θ) เป็นจุดปลายส่วนโค้งที่ยาว |θ| หน่วย โดยวัดจาก (1,0) ไปตามส่วนโค้งของวงกลม ซึ่งจะมีทั้งทิศทวนเข็มนาฬิกา และตามเข็มนาฬิกา
ต่อไปเราจะมาพิจารณา θ นะคะ
ถ้า θ ≥ 0 จะได้ว่าเป็นการวัดไปในทิศทางทวนเข็มนาฬิกา
ถ้า θ < 0 จะได้ว่าเป็นการวัดไปในทิศทางตามเข็มนาฬิกา
และเราจะให้ส่วนโค้งวงกลมหนึ่งหน่วยที่ยาว θ หน่วย มีโคออร์ดิเนทจุดปลายส่วนโค้งเป็น (x, y) นั่นคือ P(θ) = (x, y)
ตอนนี้เราก็รู้วิธีการวัดความยาวของวงกลมหนึ่งหน่วยแล้วนะคะ ต่อไปเราจะมาลองทำแบบฝึกการเขียนกราฟวงกลมหนึ่งหน่วยแสดงจุดปลายส่วนโค้ง
พิกัดจุดปลายส่วนโค้ง
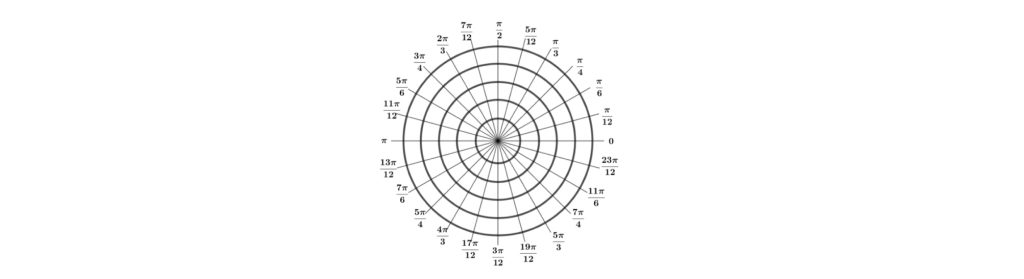
ในหัวข้อนี้พี่มาบอกวิธีการดูพิกัดจุด ว่าทำไมความยาวส่วนโค้งแต่ละพิกัดจุดที่เริ่มจากจุด(1, 0) ถึงเป็นดังรูป
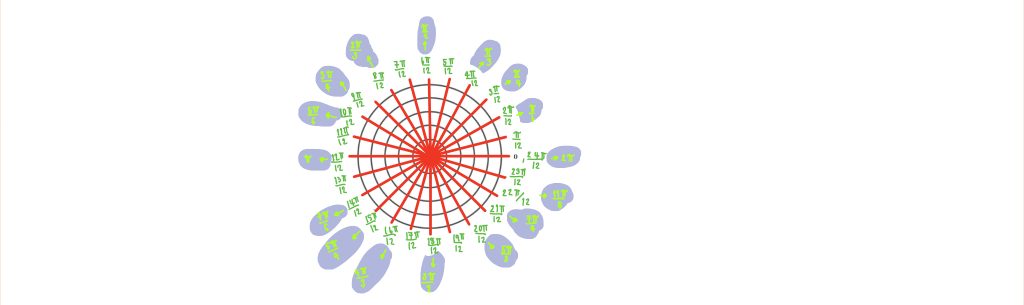
เมื่อเราแบ่งวงกลมหนึ่งหน่วยออกเป็น 24 ส่วนเท่าๆกัน จะได้ว่า พิกัดจุดปลายส่วนแรกมีความยาวเป็น =
คือ ความยาวเส้นรอบวงของวงกลมหนึ่งหน่วย แต่เรามองความยาวถึงแค่ 1 ส่วน ใน 24 ส่วน จึงต้องหารด้วย 24)
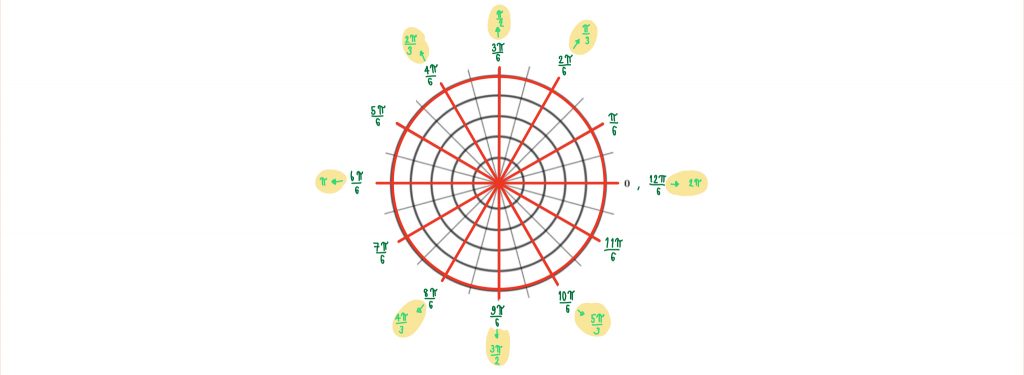
เมื่อแบ่งวงกลมหนึ่งหน่วยออกเป็น 12 ส่วนเท่าๆกัน จะได้ว่าจุดปลายส่วนแรกมีความยาวเป็น และจุดต่อไปก็จะเป็น
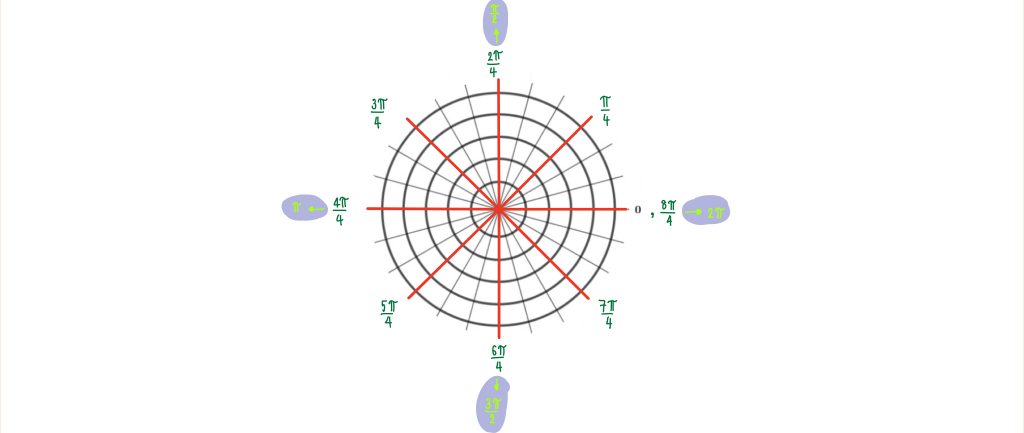
เมื่อเราแบ่งวงกลมออกเป็น 8 ส่วนเท่าๆกัน จะได้ว่า จุดปลายส่วนแรกมีความยาวเป็น
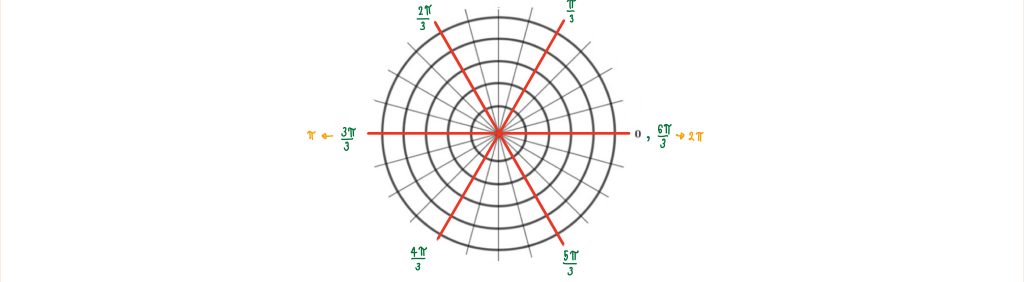
เมื่อเราแบ่งวงกลมออกเป็น 6 ส่วนเท่าๆกัน จะได้ว่าจุดปลายส่วนแรกมีความยาวเป็น
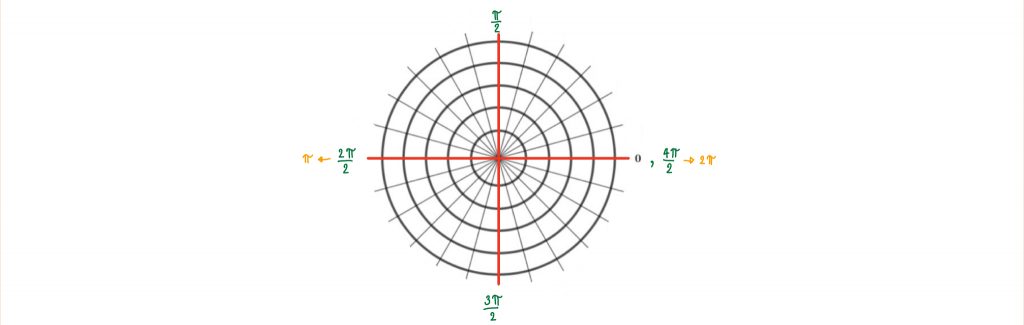
เมื่อเราแบ่งวงกลมออกเป็น 4 ส่วนเท่าๆกัน จะได้ว่าจุดปลายส่วนแรกมีความยาวเป็น
นอกจากนี้เรายังสามารถแบ่งวงกลมเป็นส่วนให้เล็กลงไปอีกนอกเหนือจากที่กล่าวมาได้ เช่น อาจจะแบ่งเป็น 28 ส่วนเท่าๆกัน ก็จะได้จุดแรกมีความยาวเป็น
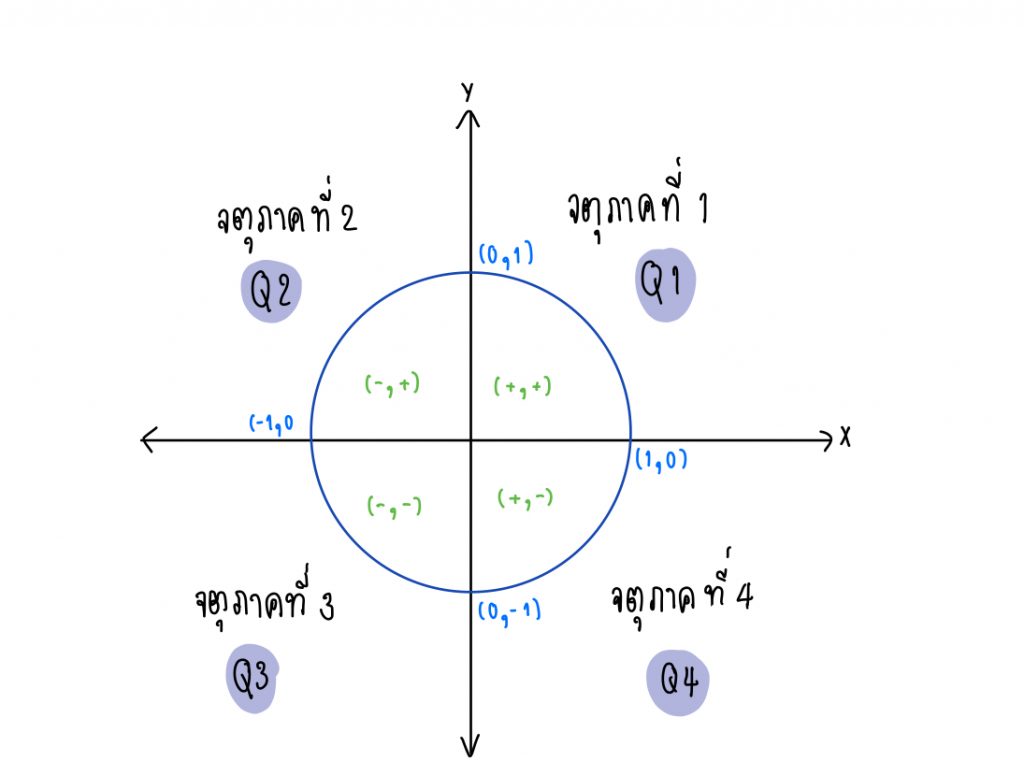
นอกจากน้องๆจะต้องรู้ความยาวส่วนปลายแล้ว สิ่งที่ต้องรู้อีกอย่างหนึ่งคือ จตุภาค (quadrant) ซึ่งจะแบ่งเป็น 4 จตุภาค

(+, +) คือ ค่า x และ y เป็นจำนวนบวก
(-, -) คือ ค่า x และ y เป็นจำนวนลบ
(-, +) คือ ค่า x เป็นจำนวนลบ ค่า y เป็นจำนวนบวก
(+, -) คือ ค่า x เป็นจำนวนบวก ค่า y เป็นจำนวนลบ
เรามาดูตัวอย่างกันนะคะ

จากรูป เราจะได้ว่า จุด P() อยู่ควอดรันต์ที่ 1
จุด P() อยู่ควอดรันต์ที่ 2
จุด P() อยู่ควอดรันต์ที่ 3
จุด P() อยู่ควอดรันต์ที่ 4



















