สถิติ (ค่ากลางของข้อมูล/การกระจายของข้อมูล)

Nidtaya

การกระจายของข้อมูล, คณิตศาสตร์, คณิตศาสตร์ ม.3, ค่ากลางของข้อมูล, ค่าเฉลี่ยเลขคณิต, ฐานนิยม, มัธยฐาน, สถิติ, ส่วนเบี่ยงเบนมาตรฐาน

Add LINE friends for one click to find article.

บทความนี้ได้รวบรวมความรู้เรื่อง ค่ากลางของข้อมูลและการกระจายของข้อมูล ซึ่งค่ากลางของข้อมูลจะประกอบด้วย ค่าเฉลี่ยเลขคณิต มัธยฐาน และฐานนิยม ส่วนการวัดการกระจายของข้อมูลจะศึกษาในเรื่องการหาส่วนเบี่ยงเบนมาตรฐาน ซึ่งน้องๆสามารถทบทวน การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ ได้ที่ ⇒⇒ การนำเสนอข้อมูลในรูปตารางแจกแจงความถี่ ⇐⇐

หมายเหตุ ค่าเฉลี่ยในทางคณิตศาสตร์มีหลายชนิด แต่ที่นิยมใช้คือค่าเฉลี่ยเลขคณิต

การวัดค่ากลางของข้อมูล เป็นการหาค่ากลางมาเป็นตัวแทนของข้อมูลแต่ละชุด ซึ่งมีวิธีการหาได้หลายวิธีที่นิยมกัน ได้แก่

ค่าเฉลี่ยเลขคณิต
มัธยฐาน
ฐานนิยม

ค่าเฉลี่ยเลขคณิต (Arithmetic mean)

ค่าเฉลี่ยเลขคณิต คือ ค่าของผลรวมของค่าสังเกตของข้อมูลทั้งหมดหารด้วยจำนวนข้อมูลทั้งหมด เรียกสั้นๆ ว่า ค่าเฉลี่ย ซึ่งในการหาค่าเฉลี่ยเลขคณิตจะประกอบด้วยการหาค่าเฉลี่ยของข้อมูลที่ไม่ได้แจกแจงความถี่ และ การหาค่าเฉลี่ยของข้อมูลที่แจกแจงความถี่

การหาค่าเฉลี่ยเลขคณิตของข้อมูลที่ไม่แจกแจงความถี่

(ข้อมูลไม่ได้จัดอยู่ในรูปตารางแจกแจงความถี่) มีสูตร ดังนี้

ค่าเฉลี่ยเลขคณิต = ผลรวมของข้อมูลทั้งหมด ⁄จำนวนของข้อมูล

หรือ ผลรวมของข้อมูล = ค่าเฉลี่ยเลขคณิต x จำนวนของข้อมูล

หรือ จำนวนข้อมูลทั้งหมด = ผลรวมของข้อมูลทั้งหมด ⁄ ค่าเฉลี่ยเลขคณิต

ตัวอย่างที่ 1 จงหาค่าเฉลี่ยเลขคณิตของข้อมูล 20 22 25 27 24 28 26 28

วิธีทำ ค่าเฉลี่ยเลขคณิต = ผลรวมของข้อมูลทั้งหมด ⁄จำนวนของข้อมูล

ค่าเฉลี่ยเลขคณิต = $\frac{20+22+25+27+24+28+26+28}{8}$

= $\frac{200}{8}$

= 25

ดังนั้น ค่าเฉลี่ยเลขคณิต คือ 25

ตัวอย่างที่ 2 อนันต์ทดสอบเก็บคะแนนวิชาคณิตศาสตร์ 3 ครั้ง คือ 18 15 16 อยากทราบว่าอนันต์ทดสอบเก็บคะแนนได้คะแนนเฉลี่ยเท่าไร

วิธีทำ อนันต์ได้คะแนนเฉลี่ย = $\frac{18+15+16}{3}$

= $\frac{49}{3}$

≈ 16.33

ดังนั้น อนันต์ทดสอบเก็บคะแนนได้คะแนนเฉลี่ยประมาณ 16.33

ตัวอย่างที่ 3 ในค่ายมวยแห่งหนึ่งมีนักมวยทั้งหมด 6 คน โดยที่นักมวยแต่ละคนมีน้ำหนักคิดเป็น

ปอนด์ ดังนี้ 125, 303, 163, 175, 181, 220 จงหาค่าเฉลี่ยเลขคณิตของน้ำหนักของนักมวยในค่ายนี้

วิธีทำ น้ำหนักเฉลี่ยต่อคน = $\frac{125+330+163+175+181+220}{6}$

= $\frac{1194}{6}$

= 199

ดังนั้น ค่าเฉลี่ยเลขคณิตของน้ำหนักของนักมวยในค่ายนี้เท่ากับ 199 ปอนด์

ตัวอย่างที่ 4 เลือกนักเรียนในชนบทแห่งหนึ่งมาจำนวน 10 คน ปรากฏว่ามีรายได้ต่อวันคิดเป็นบาทดังนี้ 85, 70, 10, 75, 44, 80, 42, 45, 40, 36 จงหาค่าเฉลี่ยเลขคณิตของรายได้ของนักเรียนดังกล่าว

วิธีทำ รายได้เฉลี่ยต่อวัน = $\frac{85+70+10+75+44+80+42+45+40+36}{10}$

= $\frac{567}{10}$

= 56.7

ดังนั้น ค่าเฉลี่ยเลขคณิตของรายได้ของนักเรียนเท่ากับ 56.7 บาทต่อวัน

ตัวอย่างที่ 5 ข้อมูลชุดหนึ่งมี 9 จำนวน ถ้าค่าเฉลี่ยเลขคณิตของข้อมูลชุดนี้เท่ากับ 4.5 ผลรวมของ

ข้อมูลชุดนี้เท่ากับเท่าใด

วิธีทำ จากสูตร ผลรวมของข้อมูล = ค่าเฉลี่ยเลขคณิต x จำนวนของข้อมูล

จะได้ ผลรวมของข้อมูล = 9 x 4.5

= 40.5

ดังนั้น ผลรวมของข้อมูลชุดนี้เท่ากับ 40.5

ตัวอย่างที่ 6 ในการทดสอบเก็บคะแนน อาริสาสอบได้ 76, 84 และ 73 คะแนน ตามลำดับ จงหาว่าในการสอบครั้งที่ 4 อาริสาจะต้องสอบให้ได้กี่คะแนนจึงจะทำให้ค่าเฉลี่ยเลขคณิตของคะแนนสอบทั้งสี่ครั้งเป็น 80 คะแนน

วิธีทำ จาก ค่าเฉลี่ย = $\frac{X_{1}+X_{2}+X_{3}+X_{4}}{n}$

จะได้ 80 = $\frac{76+84+73+X_{4}}{4}$

80 x 4 = 233 + X₄

320 = 233 + X₄

X₄ = 320 – 233

X₄ = 87

ดังนั้น ในการสอบครั้งที่ 4 อาริสาจะต้องสอบได้ 87 คะแนน

การหาค่าเฉลี่ยเลขคณิตของข้อมูลที่แจกแจงความถี่

(ในรูปตารางที่เป็นช่วงหรืออันตรภาคชั้น) มีสูตร ดังนี้

ค่าเฉลี่ยเลขคณิต = ∑fX ⁄ N

เมื่อ ∑ คือผลรวม , X คือ ข้อมูล , N คือ จำนวนข้อมูลหรือความถี่

ตัวอย่างที่ 7 ผลการสอบวิชาคณิตศาสตร์ของนักเรียน 20 คน เป็นดังนี้

คะแนน	15	18	20	21	25	27	30
จำนวนนักเรียน	2	3	2	4	2	1	1

จงหาค่าเฉลี่ยเลขคณิตของคะแนนสอบครั้งนี้

วิธีทำ สร้างตารางเพื่อคำนวณหาค่าเฉลี่ยเลขคณิตดังนี้

คะแนน (X)	จำนวนนักเรียน (f)	fX
15	2	15 x 2
18	3	18 x 3
20	2	20 x 2
21	4	21 x 4
25	2	25 x 2
27	1	27 x 1
30	1	30 x 1
รวม	N = 15	∑fX = 315

จาก ค่าเฉลี่ยเลขคณิต = ∑fX ⁄ N

จะได้ ค่าเฉลี่ยเลขคณิตของคะแนนสอบ = ³¹⁵⁄₁₅ = 21

ดังนั้น ค่าเฉลี่ยเลขคณิตของคะแนนสอบครั้งนี้ เท่ากับ 21 คะแนน

ตัวอย่างที่ 8 จงหาค่าเฉลี่ยของอายุชาวบ้านในชุมชนแห่งหนึ่งจำนวน 20 คน

อายุ (ปี)	จำนวนคน
11 – 15	4
16 – 20	3
21 – 25	2
26 – 30	4
31 – 35	5
36 – 40	2

วิธีทำ สร้างตารางเพื่อคำนวณหาค่าเฉลี่ยเลขคณิตดังนี้

อายุ (ปี)	จำนวนคน(f)	จุดกึ่งกลาง (X)	fX
11 – 15	4	13	52
16 – 20	3	18	54
21 – 25	2	23	46
26 – 30	4	28	112
31 – 35	5	33	165
36 – 40	2	38	76
	N = 20		∑fX = 505

จาก ค่าเฉลี่ยเลขคณิต = ∑fX ⁄ N

จะได้ ค่าเฉลี่ยเลขคณิตของคะแนนสอบ = ⁵⁰⁵⁄₂₀ = 25.25

ดังนั้น ค่าเฉลี่ยเลขคณิตของคะแนนสอบครั้งนี้ เท่ากับ 25.25 คะแนน

มัธยฐาน (Median)

มัธยฐาน คือ ค่าที่มีตำแหน่งอยู่กึ่งกลางของข้อมูลทั้งหมด เมื่อได้เรียงข้อมูลตามลำดับ ไม่ว่าจากน้อยไปมาก หรือจากมากไปน้อย แทนด้วยสัญลักษณ์ Me หรือ Med

การหามัธยฐานของข้อมูลที่ไม่ได้แจกแจงความถี่

1) เรียงข้อมูลที่มีอยู่ทั้งหมดจากน้อยไปมาก หรือมากไปน้อยก็ได้

2) ตำแหน่งมัธยฐาน คือ ตำแหน่งกึ่งกลางข้อมูลทั้งหมด

ดังนั้น ตำแหน่งของมัธยฐาน คือ เมื่อ N คือ จำนวนข้อมูลทั้งหมด

3) มัธยฐาน คือ ค่าที่มีตำแหน่งอยู่กึ่งกลางของข้อมูลทั้งหมด

ตัวอย่างที่ 9 จงหามัธยฐานของข้อมูล 2, 6, 4, 8, 12, 14, 10

วิธีทำ เรียงข้อมูลจากน้อยไปมาก จะได้ 2, 4, 6, 8, 10, 12, 14

ตำแหน่งของค่ามัธยฐาน คือ $\frac{N+1}{2}$ = $\frac{7+1}{2}$ = 4

ดังนั้น ค่ามัธยฐาน คือ 8

ตัวอย่างที่ 10 จงหามัธยฐานของข้อมูล 1, 7, 5, 11, 13, 15, 17, 9

วิธีทำ เรียงข้อมูลจากน้อยไปมาก จะได้ 1, 5, 7, 9, 11, 13, 15, 17

ตำแหน่งของค่ามัธยฐาน คือ $\frac{N+1}{2}$ = $\frac{8+1}{2}$ = 4.5

ค่ามัธยฐานของข้อมูลอยู่ระหว่างตำแหน่งที่ 4 และ 5

ดังนั้น ค่ามัธยฐาน เท่ากับ $\frac{9+11}{2}$ = ²⁰⁄₂ = 10

ฐานนิยม (Mode)

ฐานนิยม คือ ข้อมูลที่มีความถี่สูงสุดหรือปรากฏบ่อยครั้งที่สุด จะใช้กับข้อมูลเชิงคุณภาพมากกว่าเชิงปริมาณ เช่น ขนาดรองเท้า ขนาดยางรถยนต์

ตัวอย่างที่ 11 จงหาฐานนิยมของขนาดรองเท้าของนักเรียนจำนวน 15 คน ซึ่งมีขนาด 4, 4, 4, 5, 5, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9

ตอบ ฐานนิยมของขนาดรองเท้าของนักเรียนจำนวน 15 คน คือ 5 เพราะมีรองเท้าขนาด 5 มากที่สุด คือ 4 คน กล่าวคือ นักเรียนส่วนใหญ่ใช้รองเท้าขนาด 5

ตัวอย่างที่ 12 ข้อมูลชุดหนึ่งประกอบด้วย 3, 5, 8, 10, 12, 15, 16 จงหาฐานนิยม

ตอบ ไม่มีฐานนิยม เพราะ ข้อมูลแต่ละค่ามีความถี่เท่ากันหมด

ตัวอย่างที่ 13 ข้อมูลซึ่งประกอบด้วย 5, 4, 6, 6, 6, 7, 8, 8, 8, 9, 9, 9 จงหาฐานนิยม

ตอบ ไม่มีฐานนิยม เพราะ ข้อมูลมีความถี่สูงสุดเท่ากันสามค่า คือ 6, 8 และ 9

ตัวอย่างที่ 14 ข้อมูลต่อไปนี้แสดงจำนวนนักศึกษาสาขาวิชาต่างๆ ของสถาบันการศึกษาแห่งหนึ่ง

สาขาวิชา

จำนวนนักศึกษา

ศึกษาศาสตร์

นิติศาสตร์

บริหารธุรกิจ

มนุษยศาสตร์

ศิลปกรรมศาสตร์

500

400

450

350

300

จากตารางนี้ จงหาฐานนิยม

ตอบ ฐานนิยมของข้อมูลนี้ คือ สาขาวิชาศึกษาศาสตร์ เพราะ มีความถี่มากที่สุด เท่ากับ 500

ส่วนเบี่ยงเบนมาตรฐาน

ส่วนเบี่ยงเบนมาตรฐาน เป็นการวัดการกระจายของข้อมูลที่ใช้ข้อมูลทุกค่ามาคำนวณ ซึ่งเป็นวิธีการวัดการกระจายที่นิยมและเชื่อถือได้มากที่สุด การหาส่วนเบี่ยงเบนมาตรฐานของข้อมูลหาได้โดยใช้สูตรดังนี้

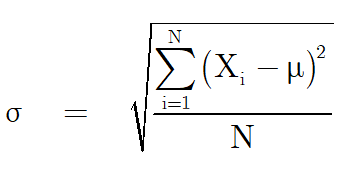
ตัวอย่างที่ 15 อุณหภูมิในจังหวัดเชียงใหม่ ซึ่งวัดทุกเช้าวันที่ 1 ของทุก ๆ เดือน ในปีที่ผ่านมาเป็นดังนี้

เดือน	ม.ค.	ก.พ.	มี.ค.	เม.ย.	พ.ค.	มิ.ย.	ก.ค.	ส.ค.	ก.ย.	ต.ค.	พ.ย.	ธ.ค.
อุณหภูมิ	2	6	10	24	23	23	22	21	21	20	14	6

จงหาส่วนเบี่ยงเบนมาตรฐานของข้อมูลชุดนี้

วิธีทำ จากโจทย์ต้องการหาส่วนเบี่ยงเบนมาตรฐานของข้อมูล

สูตรที่ใช้ในการคำนวณ คือ

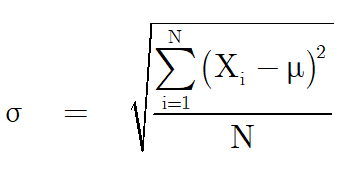
ขั้นแรก หาค่าเฉลี่ย (μ) และเราทราบจำนวนข้อมูล (N) เท่ากับ 12

ค่าเฉลี่ย (μ) = $\frac{2+6+10+24+23+23+22+21+21+20+14+6}{12}$

= ¹⁹²⁄ ₁₂ = 16

ขั้นที่สอง หาค่าของ ได้ดังนี้

X – µ

(X – µ)²

-14

-10

-6

-2

-10

196

100

= 700

จะได้ = 700

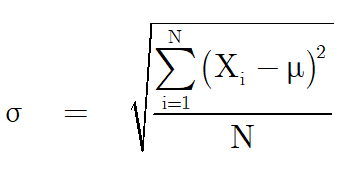และ = $\frac{\sqrt{700}}{12}$ ≈ 2.23

ดังนั้น ส่วนเบี่ยงเบนมาตรฐานของข้อมูลชุดนี้ มีค่าประมาณ 2.23

คลิปวิดีโอ

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

Preposition & Gerund เรื่องเล็กๆ ที่เจอบ๊อยบ่อย

สวัสดีน้องๆ ม. ปลายทุกคนโดยเฉพาะน้องๆ ม. 6 รุ่นโควิดนะครับ วันนี้เรามาทบทวนไวยากรณ์จุดเล็กๆ แต่สำคัญเอาเรื่องอยู่เหมือนกัน นั่นก็คือการใช้ Gerund ตามหลัง Preposition นั่นเอง ว่าแล้วก็เริ่มกันเลยดีกว่าครับ!

การวัดและความเป็นมาของการวัด

ในบทความนี้เราจะได้เรียนรู้ความเป็นมาของการวัดในหลายๆมิติ จนกระทั่งวิวัฒนาการที่ทำให้ได้ความแม่นยำในการวัดอย่างเป็นมาตรฐานมากขึ้นเรื่อยๆ

โดเมนของความสัมพันธ์

โดเมนของความสัมพันธ์ โดเมนของความสัมพันธ์ r คือ สมาชิกตัวหน้าของคู่อันดับในความสัมพันธ์ r เขียนแทนด้วย กรณีที่ r เขียนแบบแจกแจงสมาชิก เราสามารถหาโดเมนได้เลยโดย คือสมาชิกตัวหน้า เช่น = {(2, 2), (3, 4), (8, 9)} จะได้ว่า = {2, 3, 8}

อสมการ

จากบทความที่ผ่านมาได้พูดถึงเรื่องช่วงของจำนวนจริงไปแล้ว บทความนี้เราจะนำความรู้เกี่ยวกับช่วงของจำนวนจริงมาใช้ในการแก้อสมการเพื่อหาคำตอบกันนะคะ ถ้าน้องๆได้อ่านบทความนี้แล้วรับรองว่าพร้อมทำข้อสอบแน่นอนค่ะ

การให้เหตุผลแบบนิรนัย

จากบทความที่แล้วเราได้เรียนเรื่องการให้เหตุผลแบบอุปนัยไปแล้ว บทความนี้พี่จะพูดถึงการให้เหตผลแบบนิรนัย ซึ่งแน่นอนว่ามักจะเจอในข้อสอบ O-Net แต่น้องๆไม่ต้องกังวลว่าจะทำไม่ได้ หากน้องได้อ่านบทความนี้แล้วน้องๆจะทำข้อสอบเกี่ยวกับการให้เหตุผลได้แน่นอนค่ะ

แผนภูมิแท่ง และการเปรียบเทียบข้อมูล

บทความนี้จะพูดถึงการนำเสนอข้อมูลในรูปแบบของแผนภูมิแท่งไม่ว่าจะเป็นการเปรียบเทียบข้อมูล 2 จำนวน และ 3 จำนวน น้องๆจะสามารถนำข้อมูลที่สำรวจมาเขียนเป็นแผนภูมิแท่งได้และจะง่ายต่อการนำเสนอมากยิ่งขึ้น