ความน่าจะเป็นของเหตุการณ์

Nidtaya

คณิต, คณิตศาสตร์, คณิตศาสตร์ ม.3, ความน่าจะเป็น, ม.3, เหตุการณ์

Add LINE friends for one click to find article.

ความน่าจะเป็นของเหตุการณ์

บทความนี้ได้รวบรวมความรู้เรื่อง ความน่าจะเป็นของเหตุการณ์ ซึ่งได้กล่าวถึงขั้นตอนและวิธีการหาความน่าจะเป็นของเหตุการณ์ และยกตัวอย่างประกอบ อธิบายอย่างละเอียด ซึ่งก่อนจะเรียนเรื่อง ความน่าจะเป็นของเหตุการณ์น้องๆสามารถทบทวน การทดลองสุ่มและเหตุการณ์ ได้ที่ ⇒⇒ การทดลองสุ่มและเหตุการณ์ ⇐⇐

ความน่าจะเป็นของเหตุการณ์ (probability) คือ อัตราส่วนระหว่างจำนวนเหตุการณ์ที่สนใจ (n(E)) กับจำนวนแซมเปิลสเปซ (n(S)) ที่มีโอกาสเกิดขึ้นได้พร้อม ๆ กัน ใช้สัญลักษณ์ “P(E)” แทนความน่าจะเป็นของการเกิดเหตุการณ์ที่สนใจ

โดยที่ n(E) แทน จำนวนผลลัพธ์ทั้งหมดของเหตุการณ์ที่เราสนใจ

n(S) แทน จำนวนผลลัพธ์ทั้งหมดที่จะเกิดขึ้นได้

P(E) แทน ความน่าจะเป็นของเหตุการณ์

ดังนั้น P(E) = $\frac{n(E)}{n(S)}$

ข้อควรจำ

0 ≤ P(E) ≤ 1
ถ้า P(E) = 0 เหตุการณ์นั้นๆ จะไม่มีโอกาสเกิดขึ้นเลย
ถ้า P(E) = 1 เหตุการณ์นั้นๆ เกิดขึ้นแน่นอน

ตัวอย่างที่ 1

ตัวอย่างที่ 1 จากการโยนลูกเต๋า 2 ลูก 1 ครั้ง จงหาความน่าจะเป็นของเหตุการณ์ต่อไปนี้

1) เหตุการณ์ที่ได้ผลรวมของแต้มมากกว่าหรือเท่ากับ 11

2) เหตุการณ์ที่ได้ผลรวมของแต้มเป็นจำนวนคู่

3) เหตุการณ์ที่ลูกเต๋าขึ้นแต้ม 1 อย่างน้อยหนึ่งลูก

วิธีทำ หา S จากการทอดลูกเต๋า 2 ลูก 1 ครั้ง ได้ดังนี้

S = { (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

n(S) = 36

1) เหตุการณ์ที่ได้ผลรวมของแต้มมากกว่าหรือเท่ากับ 11

อธิบายเพิ่มเติม : ผลรวมของแต้มมากกว่าหรือเท่ากับ 11 หมายความว่า เมื่อนำแต้มของลูกเต๋า 2 ลูกมาบวกกัน แล้วได้ผลลัพธ์เท่ากับ 11 และมากกว่า 11

ให้ E₁ แทน เหตุการณ์ที่ได้ผลรวมของแต้มมากกว่าหรือเท่ากับ 11

E₁ = { (5, 6) , (6, 5 ) , ( 6, 6) }

n (E₁) = 3

P (E₁) = $\frac{n(E_{1})}{n(S)}$ = $\frac{3}{36}$ = $\frac{1}{12}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่ได้ผลรวมของแต้มมากกว่าหรือเท่ากับ 11 เท่ากับ $\frac{1}{12}$

2) เหตุการณ์ที่ได้ผลรวมของแต้มเป็นจำนวนคู่

อธิบายเพิ่มเติม : ผลรวมของแต้มเป็นจำนวนคู่ จะต้องเกิดจากแต้มคี่ทั้งสองลูกและแต้มคู่ทั้งสองลูก

ให้ E₂ แทน เหตุการณ์ที่ได้ผลรวมของแต้มเป็นจำนวนคู่

E₂ = { (1,1) , (1,3) , (1,5) , (2,2) , (2,4) , (2,6) , (3,1) , (3,3) , (3,5) , (4,2) , (4,4) , (4,6) ,

(5,1) ,(5,3) ,(5,5),(6,2) ,(6,4) ,(6,6) }

n(E₂) = 18

P(E₂) = $\frac{18}{36}$ = $\frac{1}{2}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่ได้ผลรวมของแต้มเป็นจำนวนคู่ เท่ากับ $\frac{1}{2}$

3) เหตุการณ์ที่ลูกเต๋าขึ้นแต้ม 1 อย่างน้อยหนึ่งลูก

อธิบายเพิ่มเติม : ลูกเต๋าขึ้นแต้ม 1 อย่างน้อยหนึ่งลูก หมายความว่า ขึ้นแต้ม 1 หนึ่งลูกหรือสองลูกก็ได้

ให้ E₃ แทน เหตุการณ์ที่ลูกเต๋าขึ้นแต้ม 1 อย่างน้อยหนึ่งลูก

E₃ = { (1,1) ,(1,2) ,((1,3) ,(1,4) ,(1,5) ,(1,6) ,(2,1) ,(3,1) ,(4,1) ,(5,1) ,(6,1) }

n(E₃) = 11

P(E₃) = $\frac{11}{36}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่ลูกเต๋าขึ้นแต้ม 1 อย่างน้อยหนึ่งลูก เท่ากับ $\frac{11}{36}$

ตัวอย่างที่ 2

ตัวอย่างที่ 2 ครอบครัวครอบครัวหนึ่ง มีบุตร 2 คน จงหาความน่าจะเป็นของเหตุการณ์ต่อไปนี้

1) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรคนแรกเป็นชาย บุตรคนที่สองเป็นหญิง

2) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นหญิง 1 คน

3) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นชาย 3 คน

4) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรทั้งสองคนเป็นชายหรือหญิงก็ได้

วิธีทำ ให้ ช แทน บุตรชาย

ญ แทน บุตรหญิง

S = {(ช, ช), (ช, ญ), (ญ, ช), (ญ, ญ)}

n(S) = 4

โดยที่ สมาชิกตัวแรกของคู่อันดับแสดงผลลัพธ์ที่อาจจะเกิดขึ้นได้ของการมีบุตรคนแรก และสมาชิกตัวที่สองของคู่อันดับแสดงผลลัพธ์ที่อาจจะเกิดขึ้นได้ของการมีบุตรคนที่สอง

1) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรคนแรกเป็นชาย บุตรคนที่สองเป็นหญิง

ให้ E₁ แทน เหตุการณ์ที่ครอบครัวนี้จะมีบุตรคนแรกเป็นชาย บุตรคนที่สองเป็นหญิง

E₁ = {(ช, ญ)}

n (E₁) = 1

P (E₁) = $\frac{n(E_{1})}{n(S)}$ = $\frac{1}{4}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่ครอบครัวนี้จะมีบุตรคนแรกเป็นชาย บุตรคนที่สองเป็นหญิง เท่ากับ $\frac{1}{4}$

2) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นหญิง 1 คน

ให้ E₂ แทน เหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นหญิง 1 คน

E₂ = { (ช, ญ) , (ญ, ช)) }

n(E₂) = 2

P(E₂) = $\frac{2}{4}$ = $\frac{1}{2}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นหญิง 1 คน เท่ากับ $\frac{1}{2}$

3) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นชาย 3 คน

เนื่องจากครอบครัวนี้มีบุตรเพียง 2 คนเท่านั้น เหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นชาย 3 คน จึงเป็น 0

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่ครอบครัวนี้จะมีบุตรเป็นชาย 3 คน เท่ากับ 0

4) เหตุการณ์ที่ครอบครัวนี้จะมีบุตรทั้งสองคนเป็นชายหรือหญิงก็ได้

ให้ E₃ แทน เหตุการณ์ที่ครอบครัวนี้จะมีบุตรทั้งสองคนเป็นชายหรือหญิงก็ได้

E₃ = {(ช, ช), (ช, ญ), (ญ, ช), (ญ, ญ)}

n(E₃) = 4

P(E₃) = $\frac{4}{4}$ = 1

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่ครอบครัวนี้จะมีบุตรทั้งสองคนเป็นชายหรือหญิงก็ได้ เท่ากับ 1

ตัวอย่างที่ 3

ตัวอย่างที่ 3 โยนเหรียญ 1 เหรียญ 3 ครั้ง จงหาความน่าจะเป็นของเหตุการณ์ต่อไปนี้

1) เหตุการณ์ที่เหรียญออกหัวมากกว่าออกก้อย

2) เหตุการณ์ที่เหรียญออกก้อยติดต่อกัน

3) เหตุการณ์ที่เหรียญออกหัวอย่างน้อย 1 เหรียญ

วิธีทำ ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้จากการทดลองสุ่มนี้มี 8 แบบ ดังนี้

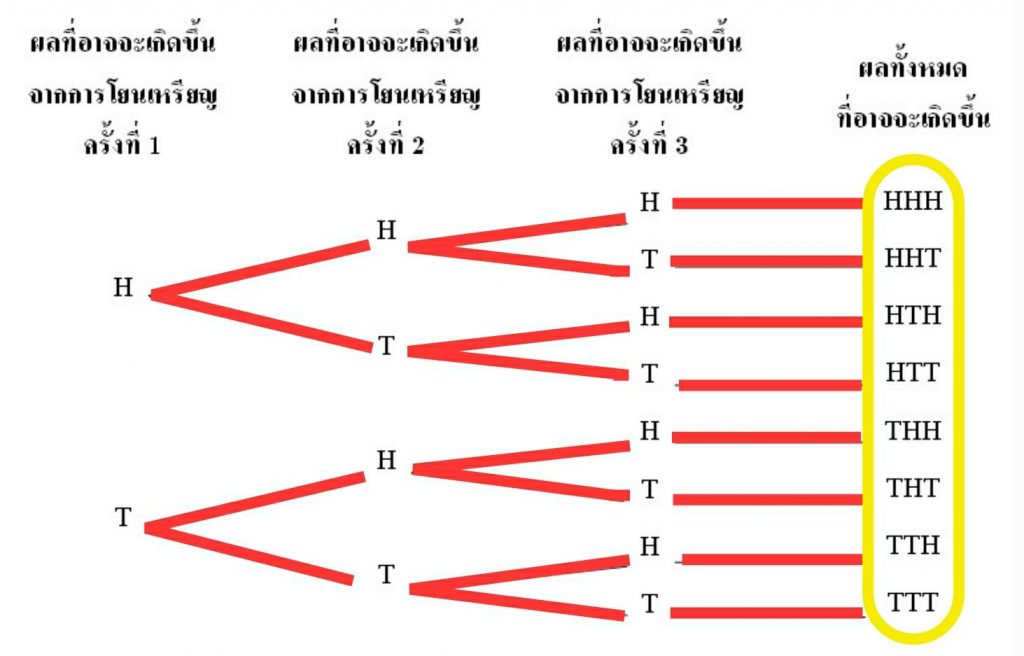
S = {HHH, HHT, HTH, HTT, THH, THT, TTH , TTT}

n(S) = 8

1) เหตุการณ์ที่เหรียญออกหัวมากกว่าออกก้อย

ให้ E₁ แทน เหตุการณ์ที่เหรียญออกหัวมากกว่าออกก้อย

E₁ = {HHH, HHT, HTH , THH}

n (E₁) = 4

P (E₁) = $\frac{n(E_{1})}{n(S)}$ = $\frac{4}{8}$ = $\frac{1}{2}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่เหรียญออกหัวมากกว่าออกก้อย เท่ากับ $\frac{1}{2}$

2) เหตุการณ์ที่เหรียญออกก้อยติดต่อกัน

ให้ E₂ แทน เหตุการณ์ที่เหรียญออกก้อยติดต่อกัน

E₂ = { HTT, TTH , TTT }

n(E₂) = 3

P(E₂) = $\frac{3}{8}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่เหรียญออกก้อยติดต่อกัน เท่ากับ $\frac{3}{8}$

3) เหตุการณ์ที่เหรียญออกหัวอย่างน้อย 1 เหรียญ

อธิบายเพิ่มเติม : เหรียญออกหัวอย่างน้อยหนึ่งเหรียญ หมายความว่า เหรียญออกหัวหนึ่งเหรียญ สองเหรียญหรือสามเหรียญก็ได้

ให้ E₃ แทน เหตุการณ์ที่ออกหัวอย่างน้อย 1 เหรียญ

E₃ = {HHH, HHT, HTH, HTT, THH, THT , TTH}

n(E₃) = 7

P(E₃) = $\frac{7}{8}$

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่เหรียญออกหัวอย่างน้อย 1 เหรียญ เท่ากับ $\frac{7}{8}$

ตัวอย่างที่ 4

ตัวอย่างที่ 4 สุ่มหยิบลูกบอล 1 ลูก จากกล่องที่มีลูกบอลสีขาว 5 ลูก จงหาความน่าจะเป็นของเหตุการณ์ต่อไปนี้

1) เหตุการณ์ที่หยิบได้ลูกบอลสีขาว

2) เหตุการณ์ที่หยิบได้ลูกบอลสีน้ำเงิน

วิธีทำ กำหนดให้ ข₁, ข₂, ข₃, ข₄ และ ข₅ แทนลูกบอลสีขาวทั้ง 5 ลูก

ผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้จากการทดลองสุ่มมี 5 แบบ คือ ข₁, ข₂, ข₃, ข₄ หรือ ข₅

นั่นคือ จำนวนผลลัพธ์ทั้งหมดที่อาจจะเกิดขึ้นได้ เท่ากับ 5 หรือ n(S) = 5

1) เหตุการณ์ที่หยิบได้ลูกบอลสีขาว

เหตุการณ์ที่หยิบได้ลูกบอลสีขาว มีผลลัพธ์ คือ ข₁, ข₂, ข₃, ข₄ หรือ ข₅

จะได้ จำนวนผลลัพธ์ของเหตุการณ์เป็น 5 หรือ n(E) = 5

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่หยิบได้ลูกบอลสีขาว เท่ากับ $\frac{5}{5}$ = 1 หรือ P(E) = 1

2) เหตุการณ์ที่หยิบได้ลูกบอลสีน้ำเงิน

เนื่องจากไม่มีลูกบอลสีน้ำเงินอยู่ภายในกล่อง

จะได้ จำนวนผลลัพธ์ที่หยิบได้ลูกบอลสีน้ำเงิน เป็น 0

ดังนั้น ความน่าจะเป็นของเหตุการณ์ที่หยิบได้ลูกบอลสีน้ำเงิน เท่ากับ 0

จาก ตัวอย่างที่ 4 จะสังเกตเห็นว่าเหตุการณ์ที่หยิบได้ลูกบอลสีขาวเป็น เหตุการณ์ที่เกิดขึ้นแน่นอน มีความน่าจะเป็นของเหตุการณ์ เท่ากับ 1 และเหตุการณ์ที่หยิบได้ลูกบอลสีน้ำเงินเป็น เหตุการณ์ที่ไม่เกิดขึ้นแน่นอน มีความน่าจะเป็น เท่ากับ 0

วิดีโอ ความน่าจะเป็นของเหตุการณ์

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

Gerund

สวัสดีค่ะนักเรียนชั้นม.5 ที่น่ารักทุกคน วันนี้เราจะไปเรียนเรื่อง “Gerund” และฝึกวิเคราะห์โจทย์ข้อสอบเข้ามหาวิทยาลัยกันจร้า พร้อมแล้วก็ไปลุยกันโลดเด้อ ความหมายของ Gerund อธิบายแบบง่ายๆ เลยว่า Gerund หรือ Ing-form ในบริติชอิงลิช ที่จริงแล้ว มันก็คือ คำกริยาเติม ing (V-ing) แล้วหน้าที่เป็นคำนาม ในภาษาไทยถูกนำมาใช้ในไวยากรณ์เรียกว่า กริยานาม นั่นเองจร้า

สมการเชิงเส้นตัวแปรเดียว

สมการเชิงเส้นตัวแปรเดียว สมการ คือ ประโยคสัญลักษณ์ที่กล่าวถึงความสัมพันธ์ของจำนวนโดยมีสัญลักษณ์ “ = ” บอกความสัมพันธ์ระหว่างจำนวน อาจมีตัวแปร หรือไม่มีตัวแปร เช่น สมการที่ไม่มีตัวแปร

การแก้อสมการเชิงเส้นตัวแปรเดียว

บทความนี้จะเป็นการสอนวิธี การแก้อสมการเชิงเส้นตัวแปรเดียว ซึ่งสามารถทำได้โดยการจัดรูปของตัวแปรให้อยู่ด้านเดียวกันและตัวเลขอยู่อีกด้าน เพื่อหาค่าของตัวแปรนั้นๆ แต่ก่อนที่น้องๆจะได้เรียนรู้การแก้อสมการนั้น น้องๆสามารถทบทวน อสมการเชิงเส้นตัวแปรเดียวเพิ่มเติมได้ที่ ⇒⇒ แนะนำอสมการเชิงเส้นตัวแปรเดียว ⇐⇐ หลักการแก้อสมการเชิงเส้นตัวแปรเดียว ในการแก้อสมการเชิงเส้นตัวแปรเดียว จะทำคล้ายๆกับการแก้สมการ โดยมีหลักการ ดังนี้ จัดตัวแปรให้อยู่ข้างเดียวกัน และจัดตัวเลขไว้อีกฝั่ง (นิยมจัดตัวแปรไว้ด้านซ้ายของสัญลักษณ์อสมการ และจัดตัวเลขไว้ด้านขวาของสัญลักษณ์อสมการ) ถ้านำจำนวนลบ มาคูณ หรือ หาร สัญลักษณ์ของอสมการจะเปลี่ยนเป็นสัญลักษณ์ตรงกันข้าม ดังนี้

$หลักการเบื้องต้นของอัตราส่วน$

หลักการเบื้องต้นของอัตราส่วน

“อัตราส่วน คือ ปริมาณ อย่างหนึ่งที่แสดงถึง จำนวน หรือ ขนาด ตามสัดส่วนเมื่อเปรียบเทียบกับอีก ปริมาณ หนึ่งที่เกี่ยวข้องกัน ที่อาจมีได้ตั้งแต่สองปริมาณขึ้นไป”

สมบัติการคูณจำนวนจริง

จากบทความก่อนหน้านี้น้องๆได้เรียนเรื่องสมบัติการบวกจำนวนจริงไปแล้ว บทความนี้พี่ก็จะพูดถึงสมบัติการคูณจำนวนจริงซึ่งมีเนื้อหาคล้ายๆกันกับการบวก และมีเพิ่มสมบัติการแจกแจงเข้ามา เนื้อหาเหล่านี้ล้วนเป็นพื้นฐานสำคัญที่จะใช้ในการเรียนเนื้อหาบทต่อๆไป เมื่อน้องๆอ่านบทความนี้แล้วน้องๆจะเรียนเนื้อหาบทต่อๆไปได้ง่ายขึ้นแน่นอนค่ะ

ป.6 Possessive pronoun โดยใช้ Whose_ Which ร่วมด้วย

การใช้ Possessive pronoun โดยใช้ Whose/ Which ร่วมด้วย

สวัสดีค่ะนักเรียนชั้นป.6 ที่น่ารักทุกคนค่ะ วันนี้เราจะไปเรียนรู้เรื่อง การใช้ Possessive pronoun โดยใช้ Whose/ Which ร่วมด้วย Let’s go! ไปลุยกันเลยจ้า Possessive pronoun คืออะไร What’s mine is yours, my dear.

ความน่าจะเป็นของเหตุการณ์

สารบัญ

ความน่าจะเป็นของเหตุการณ์

ตัวอย่างที่ 1

ตัวอย่างที่ 2

ตัวอย่างที่ 3

ตัวอย่างที่ 4

แค่ 10 นาที ก็เข้าใจได้

แนะนำ

แชร์

Gerund

สมการเชิงเส้นตัวแปรเดียว

การแก้อสมการเชิงเส้นตัวแปรเดียว

หลักการเบื้องต้นของอัตราส่วน

สมบัติการคูณจำนวนจริง

การใช้ Possessive pronoun โดยใช้ Whose/ Which ร่วมด้วย

NockAcademy

ติดต่อ

เกี่ยวกับเรา

ความช่วยเหลือ

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1

ทดลองฟรี!

เข้าใจได้ทันที NockAcademy ไลฟ์สดอันดับ 1