สามเหลี่ยมที่เท่ากันทุกประการแบบ ด้าน-มุม-ด้าน

ในบทความนี้จะกล่าวถึงหลักการของการพิสูจน์ความเท่ากันทุกประการของสามเหลี่ยมแบบ ด้าน-มุม-ด้าน

tucksaga

คณิตศาสตร์, คณิตศาสตร์ ม.2, ม.2

Add LINE friends for one click to find article.

เมื่อเราต้องการจะพิสูจน์ถึงสิ่งของใดๆว่ามีความเท่ากันทุกประการ เราจำเป็นต้องมีหลักการที่นำมาใช้ได้จริง ดังเช่นในบทความนี้ที่กล่าวถึงรูปสามเหลี่ยมที่เท่ากันทุกประการโดยใช้ความยาวของด้าน 2ด้าน และ มุม 1มุม ในการพิสูจน์

ความเท่ากันทุกประการของรูปสามเหลี่ยม

บทนิยาม รูปสามเหลี่ยม ABC คือรูปที่ประกอบด้วยส่วนของเส้นตรงสามเส้น AB, BC และ AC เชื่อมต่อจุด A, B และ C ที่ไม่อยู่บนเส้นตรงเดียวกัน เรียกจุด A, B และ C ว่า “จุดยอดมุมรูปสามเหลี่ยม ABC”

สามเหลี่ยมที่เท่ากันทุกประการ

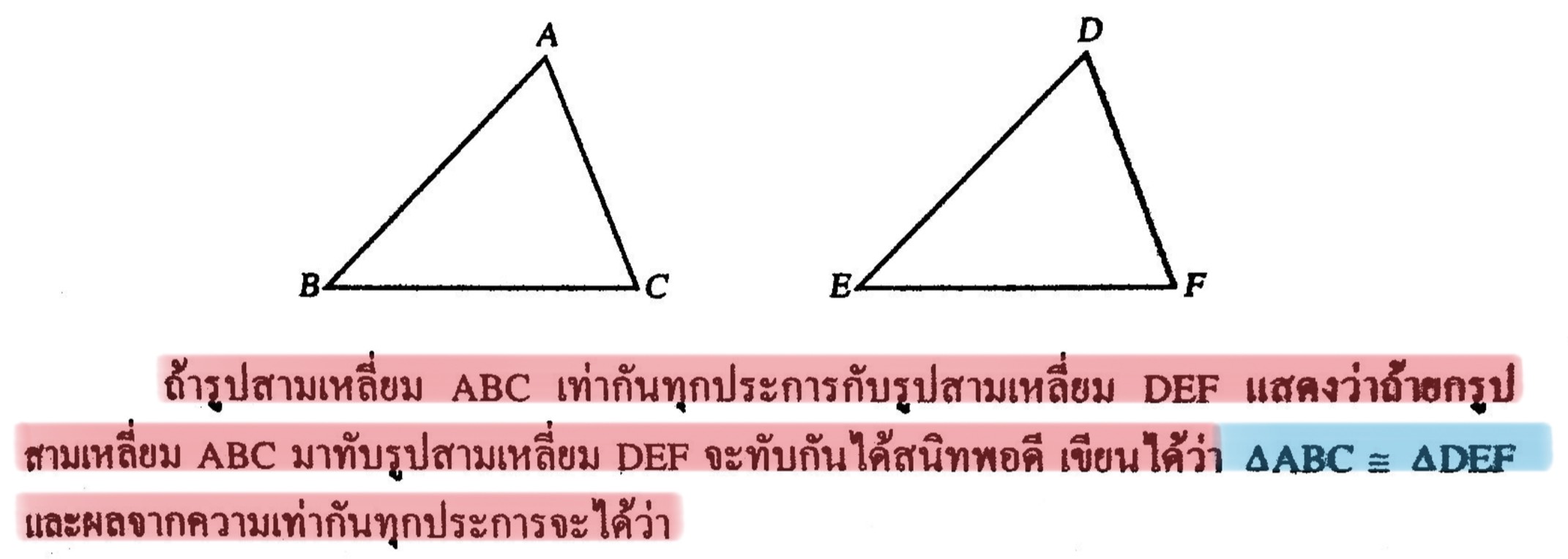
AB = DE, AC = DF และ BC = EF
<A = <D, <B = <E และ <C = <F

ลักษณะดังนี้คือ ด้านที่ยาวเท่ากัน มุมที่มีขนาดเท่ากัน หรือจุดที่ทับกันได้ เรียกว่า “สมนัยกัน”

ดังนั้น จะได้ว่ารูปสามเหลี่ยมสองรูปเท่ากันทุกประการเมื่อด้านและมุมของรูปสามเหลี่ยมมีขนาดเท่ากันเป็นคู่ๆ

ในทางกลับกัน เมื่อรูปสามเหลี่ยม ABC และรูปสามเหลี่ยม DEF มีด้านคู่ที่สมนัยกันยาวเท่ากันคือ AB = DE,
BC = EF และ CA = FD และมุมที่สมนัยกันมีขนาดเท่ากันคือ <A = <D, <B = <E และ <C= <F ดังรูป

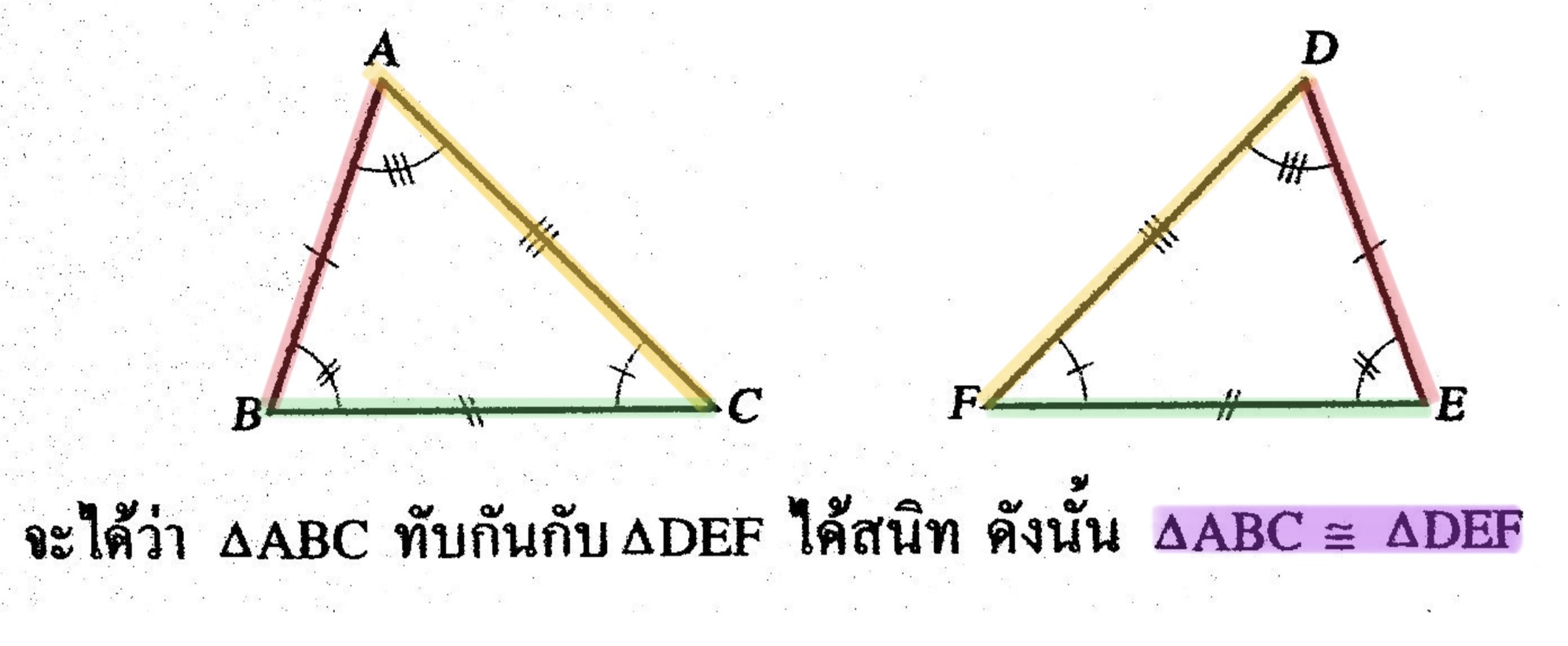
สรุปได้ว่า รูปสามเหลี่ยมสองรูปเท่ากันทุกประการก็ต่อเมื่อด้านคู่ที่สมนัยกันและมุมคู่ที่สมนัยกันของรูปสามเหลี่ยมทั้งสองรูปนั้นมีขนาดเท่ากันเป็นคู่ ๆ

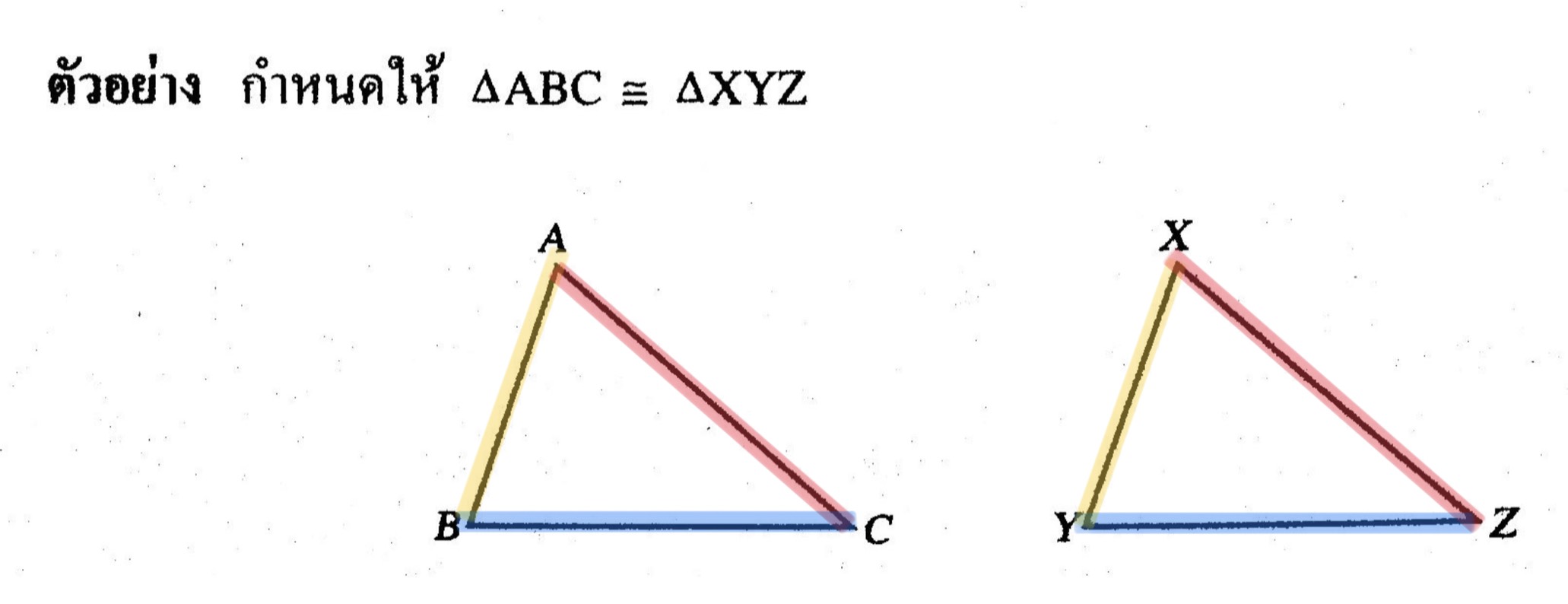
จากรูปจะได้ว่า AB สมนัยกับ XY

AC สมนัยกับ XY

BC สมนัยกับ YZ

<A สมนัยกับ <X

<B สมนัยกับ <Y

<C สมนัยกับ <Z

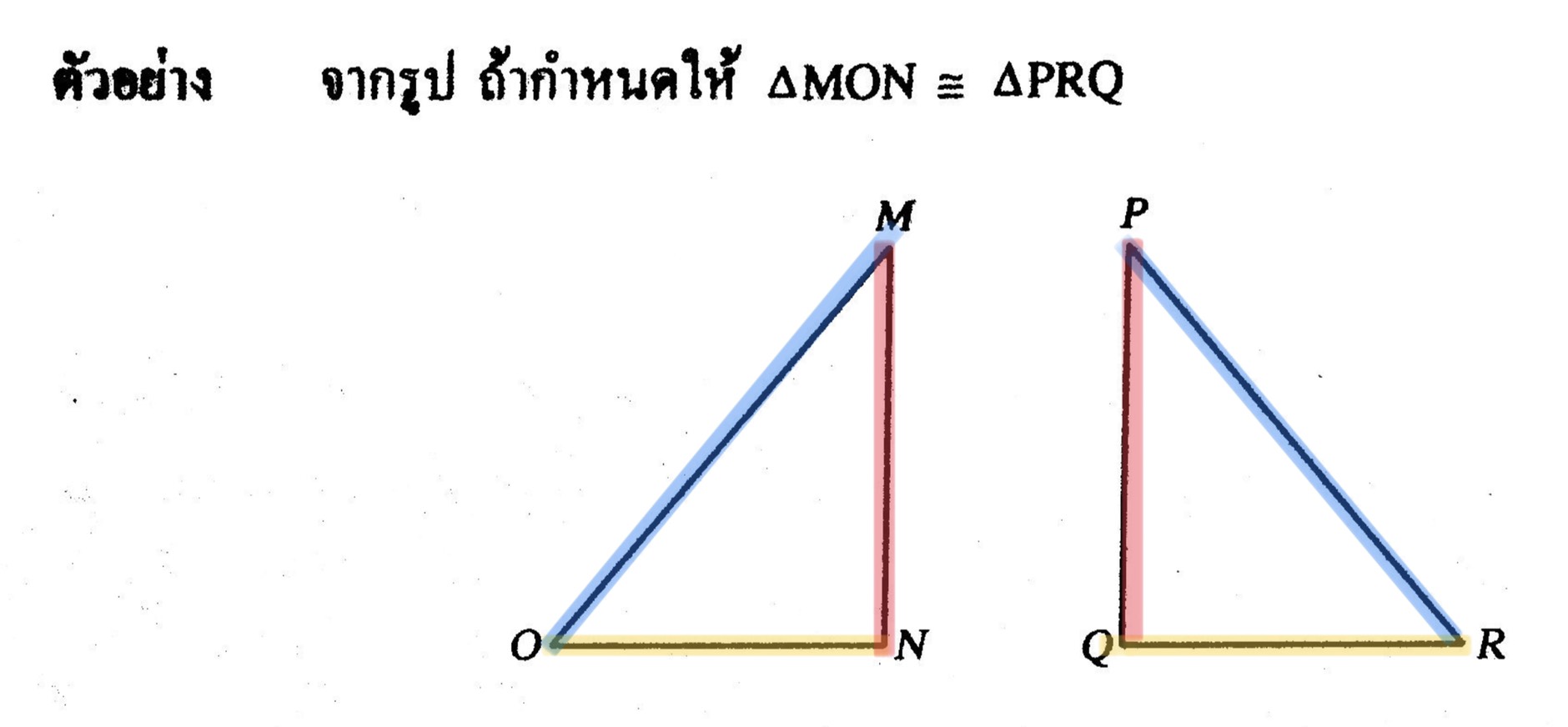
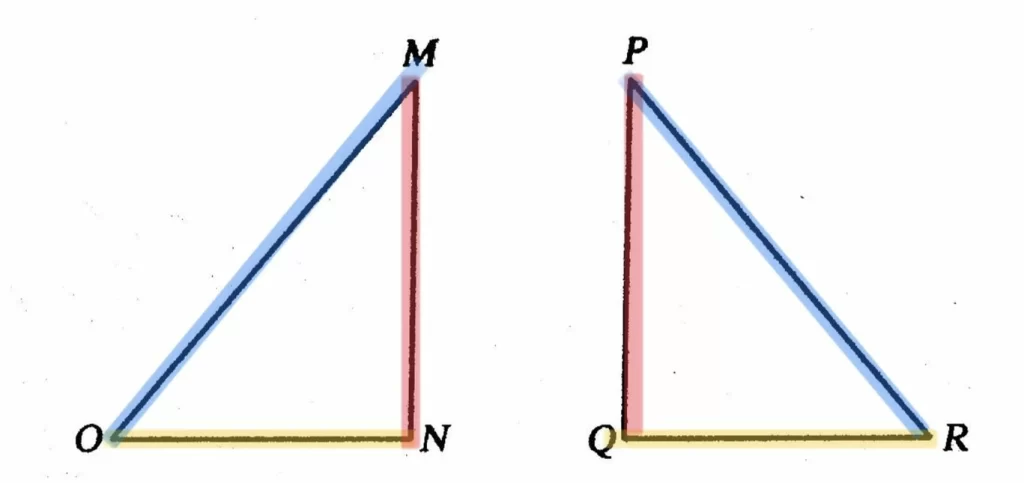
จากรูปจะได้ว่า MN = PQ

MO = PR

ON = QR

<M = <P

<O = <R

<N = <Q

รูปสามเหลี่ยมที่สัมพันธ์กันแบบด้าน-มุม-ด้าน

ในกรณีที่ต้องการทราบว่าสามเหลี่ยมสองรูปใดเท่ากันทุกประการโดยไม่จำเป็นต้องยกมาทับกัน เราสามารถใช้หลักการทางเรขาคณิตในการพิสูจน์ โดยอาศัยค้านกับมุมที่เท่ากันสามคู่ทั้งนี้ต้องขึ้นอยู่กับกรณีที่เป็นไปได้และถือเป็นสัจพจน์ ดังต่อไปนี้

ถ้ารูปสามเหลี่ยมสองรูปใด ๆ มีด้านยาวเท่ากันสองคู่และมุมในระหว่างด้านคู่ที่ยาวเท่ากันมีขนาดเท่ากันแล้ว ผลที่ตามมาคือ ด้านที่สมนัยที่เหลืออีก 1 คู่จะยาวเท่ากัน และมุมที่สมนัยกันที่เหลืออีก 2 คู่จะมีขนาดเท่ากันเป็นคู่ ๆ

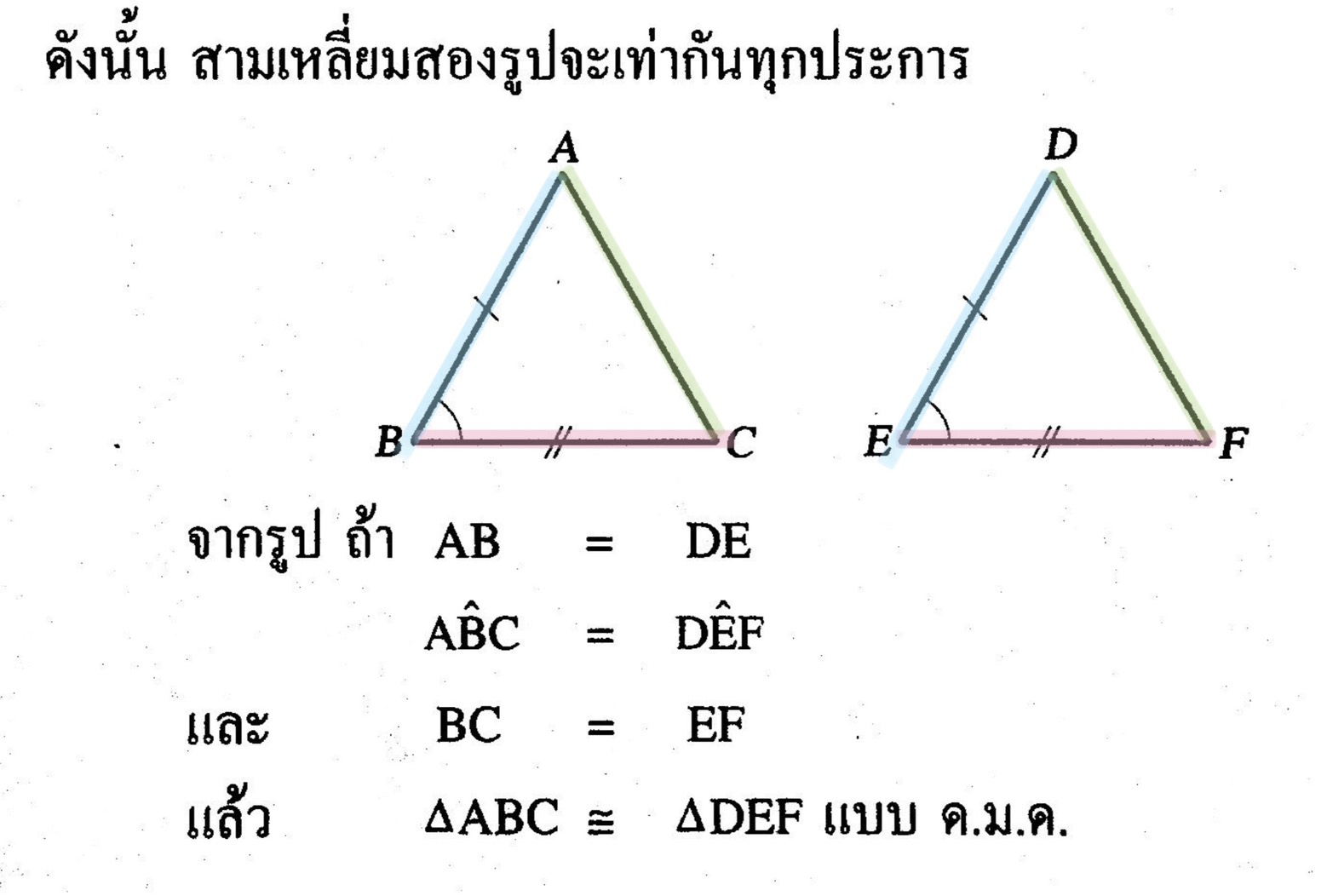
สรุปได้ว่า

ถ้ารูปสามเหลี่ยมสองรูปมีความสัมพันธ์กันแบบด้าน-มุม-ด้าน (ด.ม.ด. ) กล่าวคือ มีด้านยาวเท่ากันสองคู่ และมุมในระหว่างด้านคู่ที่ยาวเท่ากันมีขนาดเท่ากัน แล้วรูปสามเหลี่ยมสองรูปนั้นเท่ากันทุกประการ

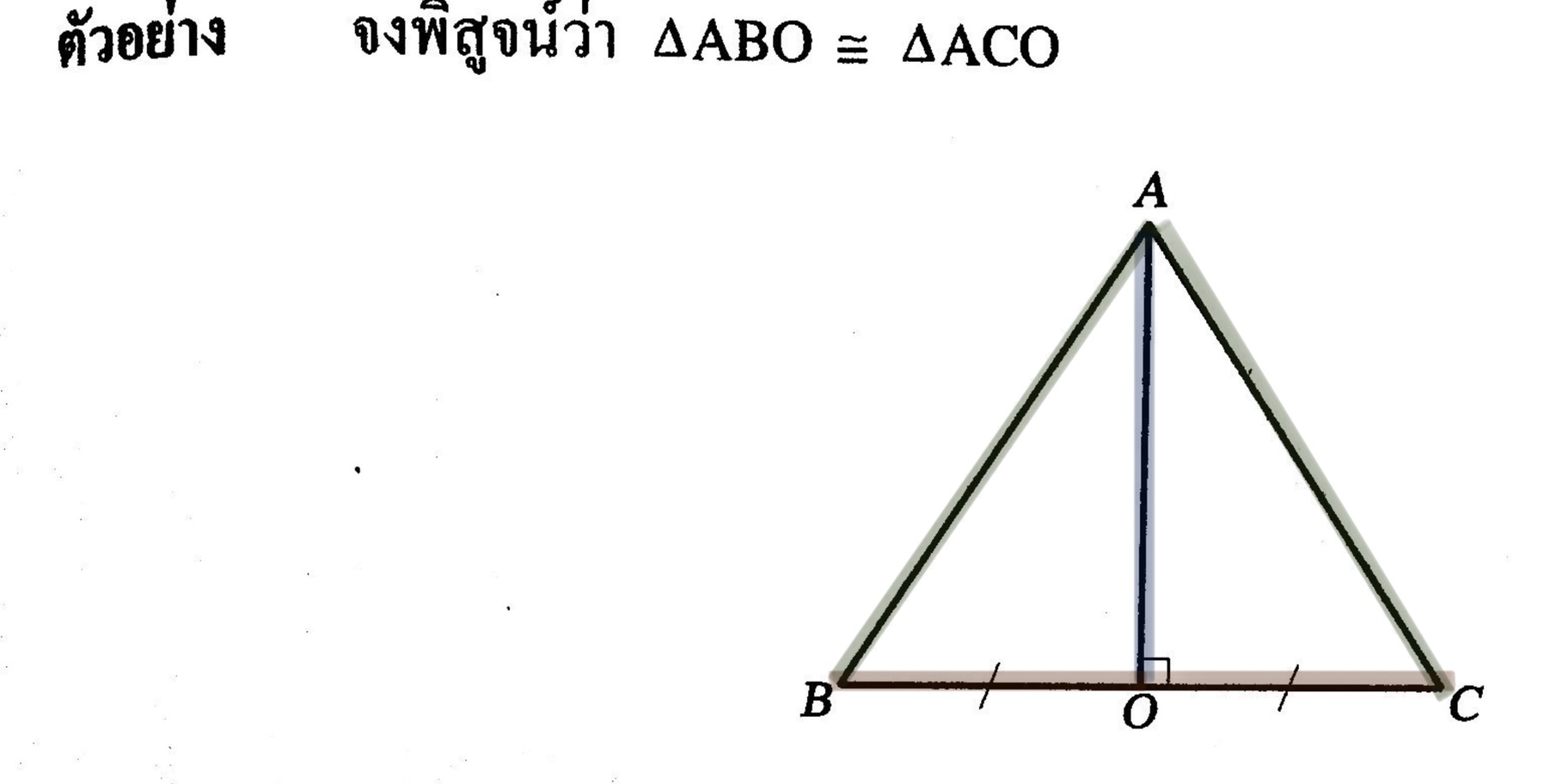
พิสูจน์ เนื่องจาก 1) ด้าน BO = ด้าน OC (กำหนดให้)

2) มุม AOB =มุม AOC (ต่างเท่ากับ 90องศา)
3) ด้าน AO = ด้าน OA (เป็นด้านร่วม)

ดังนั้น สามเหลี่ยมABO เท่ากันทุกประการกับสามเหลี่ยมACO (ด.ม.ด.)

คลิปตัวอย่างเรื่องสามเหลี่ยมที่เท่ากันทุกประการแบบ ด้าน-มุม-ด้าน

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

ทริคสังเกต ประโยคในภาษาไทย รู้ไว้ไม่สับสน

น้อง ๆ หลายคนคงจะเคยสับสนและมีข้อสงสัยเกี่ยวกับประโยคในภาษาไทยกันมาไม่มากก็น้อย ทำไมอยู่ดี ๆ เราถึงไม่เข้าใจประโยคภาษาไทยที่พูดกันอยู่ทุกวันไปได้นะ? แต่ไม่ต้องกังวลไปนะคะ บทเรียนภาษาไทยในวันนี้จะพาน้อง ๆ กลับไปทบทวนเกี่ยวกับเรื่องประโยคอีกครั้ง พร้อมเรียนรู้เคล็ดลับการสังเกตประโยคง่าย ๆ จะเป็นอย่างไร ไปดูพร้อมกันเลยค่ะ ความหมายของประโยค ประโยค เป็นหน่วยทางภาษาที่เกิดจากการนำคำหลาย ๆ คำ หรือกลุ่มคำ มาเรียงต่อกันอย่างเป็นระบบ มีความสัมพันธ์กัน

เรียนรู้บทร้องกรองสุภาษิต ตนเป็นที่พึ่งแห่งตน

การนำสุภาษิตมาแต่งเป็นบทร้อยกรอง เรียกว่า บทประพันธ์ร้อยกรองสุภาษิต ซึ่งบทที่น้อง ๆ จะได้เรียนกันในวันนี้คือบทร้อยกรองสุภาษิตเรื่อง ตนเป็นที่พึ่งแห่งตน เราไปดูกันเลยค่ะว่าที่มจากของบทร้อยกรองนี้จะเป็นอย่างไร มาจากสุภาษิตอะไร รวมไปถึงถอดความหมายตัวบท ศึกษาคำศัพท์ที่น่ารู้และศึกษาคุณค่าที่อยู่ในเรื่องด้วยค่ะ ถ้าพร้อมแล้วเราไปดูพร้อมกันเลย ความเป็นมา ตนเป็นที่พึ่งแห่งตน ตนเป็นที่พึ่งแห่งตน ผู้แต่งคือ นายเพิ่ม สวัสดิ์วรรณกิจ เป็นบทร้อยกรองประเภทกลอนแปด พิมพ์รวมอยู่ในหนังสือบทประพันธ์อธิบายสุภาษิตของวรรณคดีสมาคมแห่งประเทศไทย

โจทย์ปัญหาบวก ลบ ทศนิยม

บทความนี้จะยกตัวอย่างโจทย์ปัญหาการบวกลบทศนิยม เพื่อให้น้องๆได้ทำความเข้าใจและศึกษาการแสดงวิธีคิด หากต้องไปเจอการแก้โจทย์ปัญหาในห้องเรียนจะสามารถนำความรู้จากบทความนี้ไปใช้ให้เกิดประโยชน์อย่างสูงสุด

สัดส่วน

บทความนี้ได้รวบรวมความรู้เรื่อง สัดส่วน รวมทั้งโจทย์ปัญหาเกี่ยวกับสัดส่วน ซึ่งได้รวบรวมเนื้อหาและเขียนอธิบายไว้อย่างชัดเจน รวมถึงมีคลิปวิดีโอการสอน เพื่ออำนวยความสะดวกให้กับน้องๆ สามารถเรียนรู้ได้ทุกที่ทุกเวลา แต่ก่อนจะเรียนรู้เรื่องสัดส่วนนั้น น้องๆจำเป็นต้องมีความรู้ในเรื่อง อัตราส่วนของจำนวนหลายๆจำนวน สามารถศึกษาเพิ่มเติมได้ที่ ⇒⇒ อัตราส่วนของจำนวนหลายๆจำนวน ⇐⇐ สัดส่วน สัดส่วน คือ ประโยคที่แสดงการเท่ากันของอัตราส่วนสองอัตราส่วน อัตราส่วนทั้งสองมีความสัมพันธ์ไปในทิศทางเดียวกันหรือในทิศทางตรงกันข้ามก็ได้ ชนิดของสัดส่วน สัดส่วนมี 2 ชนิด คือ สัดส่วนตรง และ สัดส่วนผกผัน

M2 V. to be + ร่วมกับ Who WhatWhere + -Like + infinitive

การใช้ V. to be ร่วมกับ Who/ What/Where และ Like +V. infinitive

สวัสดีค่ะนักเรียนชั้นม.2 ทุกคน วันนี้เราจะไปเรียนรู้เรื่อง การใช้ V. to be + ร่วมกับ Who/ What/Where + -Like + infinitive ซึ่งเป็นโครงสร้างที่สับสนบ่อย แต่ที่จริงแล้วง่ายมากๆ ไปลุยกันเลยจ้า Let’s go ความหมาย Verb to be

อัตราส่วนของจำนวนหลายๆ จำนวน

ในบทความนี้เราจะได้เรียนรู้หลักการเขียนอัตราส่วนแทนการเปรียบเทียบปริมาณของสิ่งต่างๆที่มากกว่า 2 สิ่งขึ้นไปได้ โดยใช้ความรู้เกี่ยวกับอัตราส่วนของจํานวนหลายๆจํานวนในการแก้ปัญหาหรือสถานการณ์ต่าง ๆได้

สามเหลี่ยมที่เท่ากันทุกประการแบบ ด้าน-มุม-ด้าน

สารบัญ