เมื่อเราต้องการจะพิสูจน์ถึงสิ่งของใดๆว่ามีความเท่ากันทุกประการ เราจำเป็นต้องมีหลักการที่นำมาใช้ได้จริง ดังเช่นในบทความนี้ที่กล่าวถึงรูปสามเหลี่ยมที่เท่ากันทุกประการโดยใช้ความยาวของด้าน 3 ด้าน ในการพิสูจน์
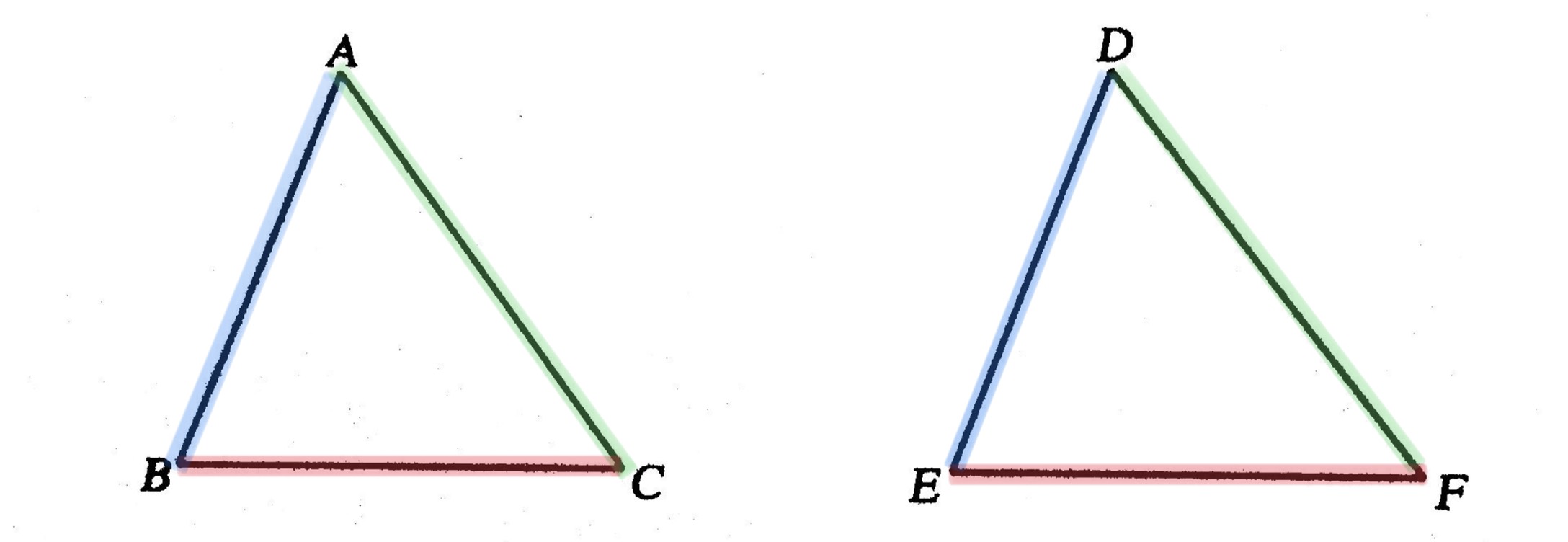
สามเหลี่ยมที่เท่ากันทุกประการแบบ ด้าน-ด้าน-ด้าน
ในทางคณิตศาสตร์เมื่อสามารถเคลื่อนที่รูปเรขาคณิตรูปหนึ่งไปทับรูปเรขาคณิตอีกรูปหนึ่งได้สนิท จะกล่าวว่ารูปเรขาคณิตสองรูปนั้น เท่ากันทุกประการ
ถ้ารูปสามเหลี่ยมสองรูปใดๆ มีด้านยาวเท่ากันสามคู่แล้ว รูปสามเหลี่ยมสองรูปนั้นจะเท่ากันทุกประการ

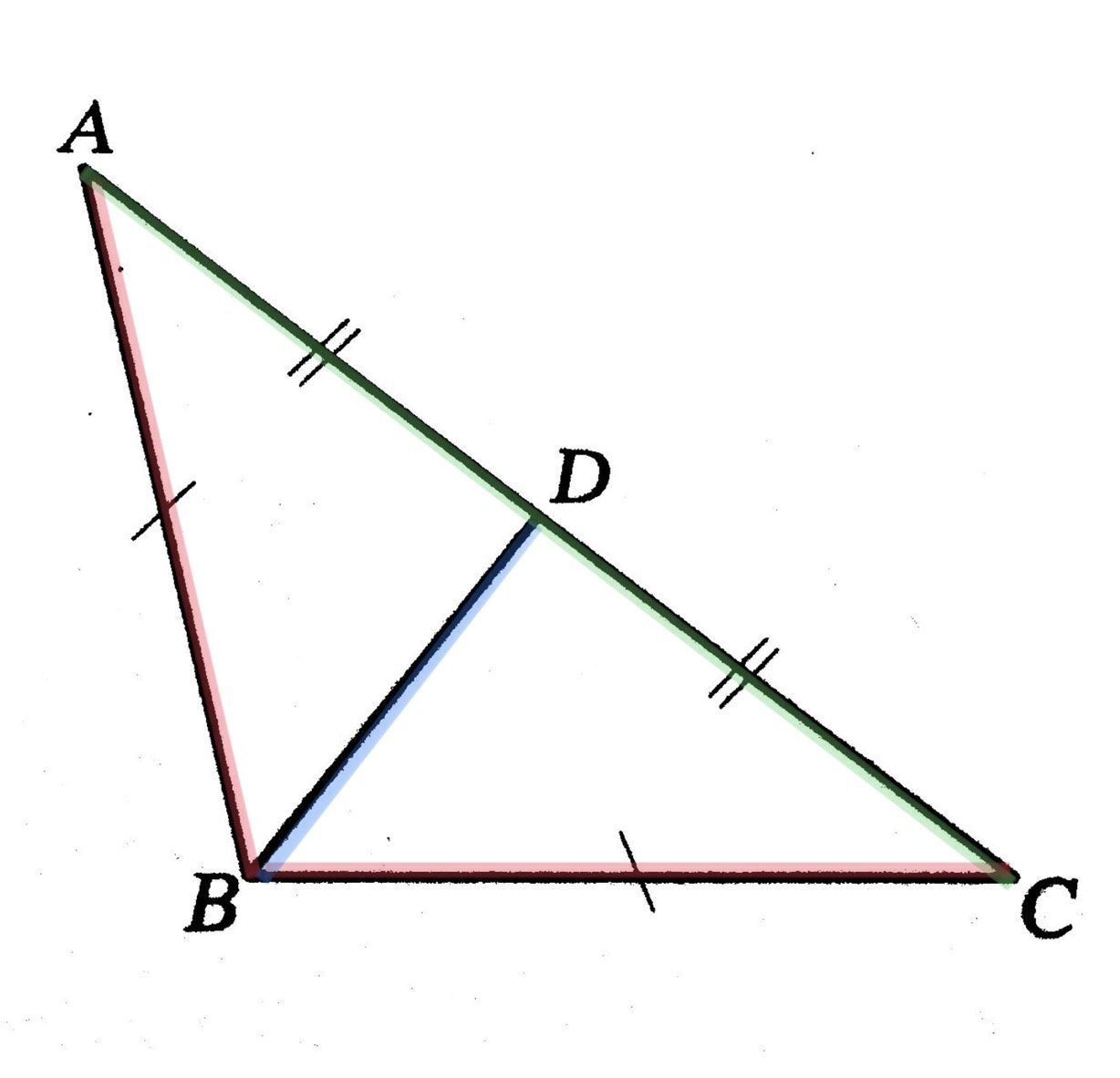
ตัวอย่างที่ 1
จากรูป จงพิสูจน์ว่า BD แบ่งครึ่ง มุมABC

ตัวอย่างที่ 2
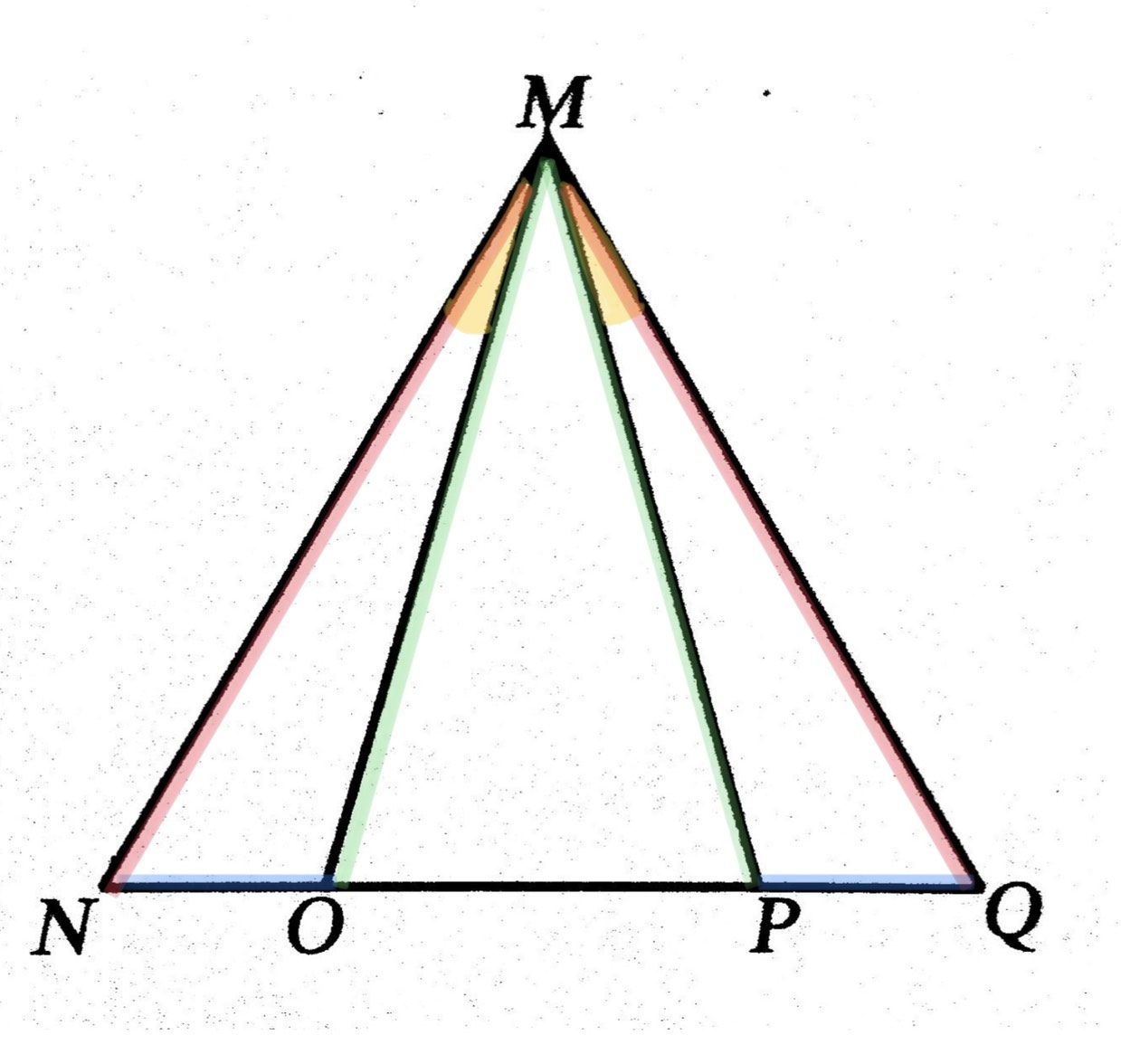
กำหนดให้สามเหลี่ยมMNQ และสามเหลี่ยมMOP เป็นรูปสามเหลี่ยมหน้าจั่ว 2รูป ที่ NO = PQ ให้พิสูจน์ว่า มุมNMO = มุมPMQ โดยใช้ความสัมพันธ์แบบ ด้าน-ด้าน-ด้าน
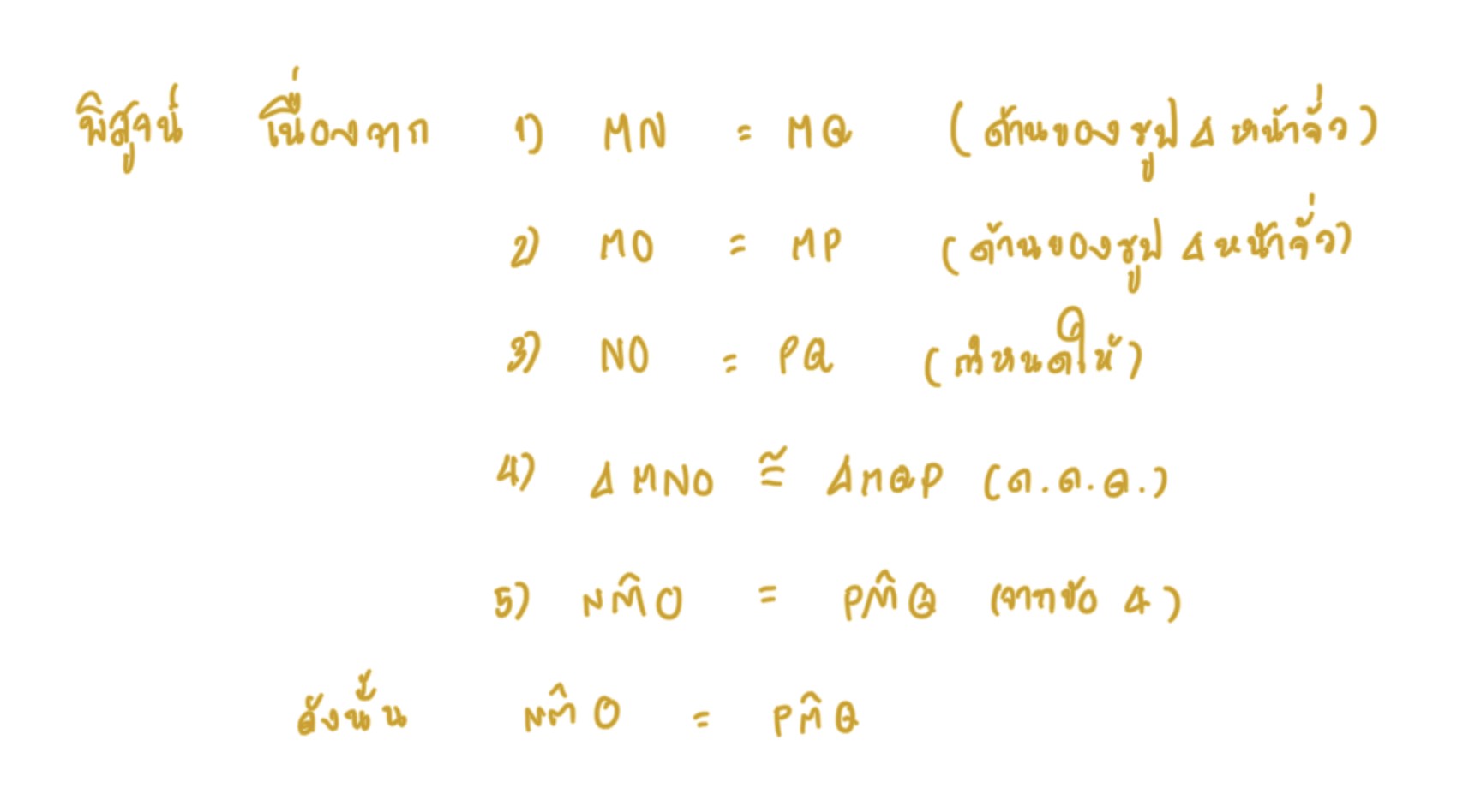
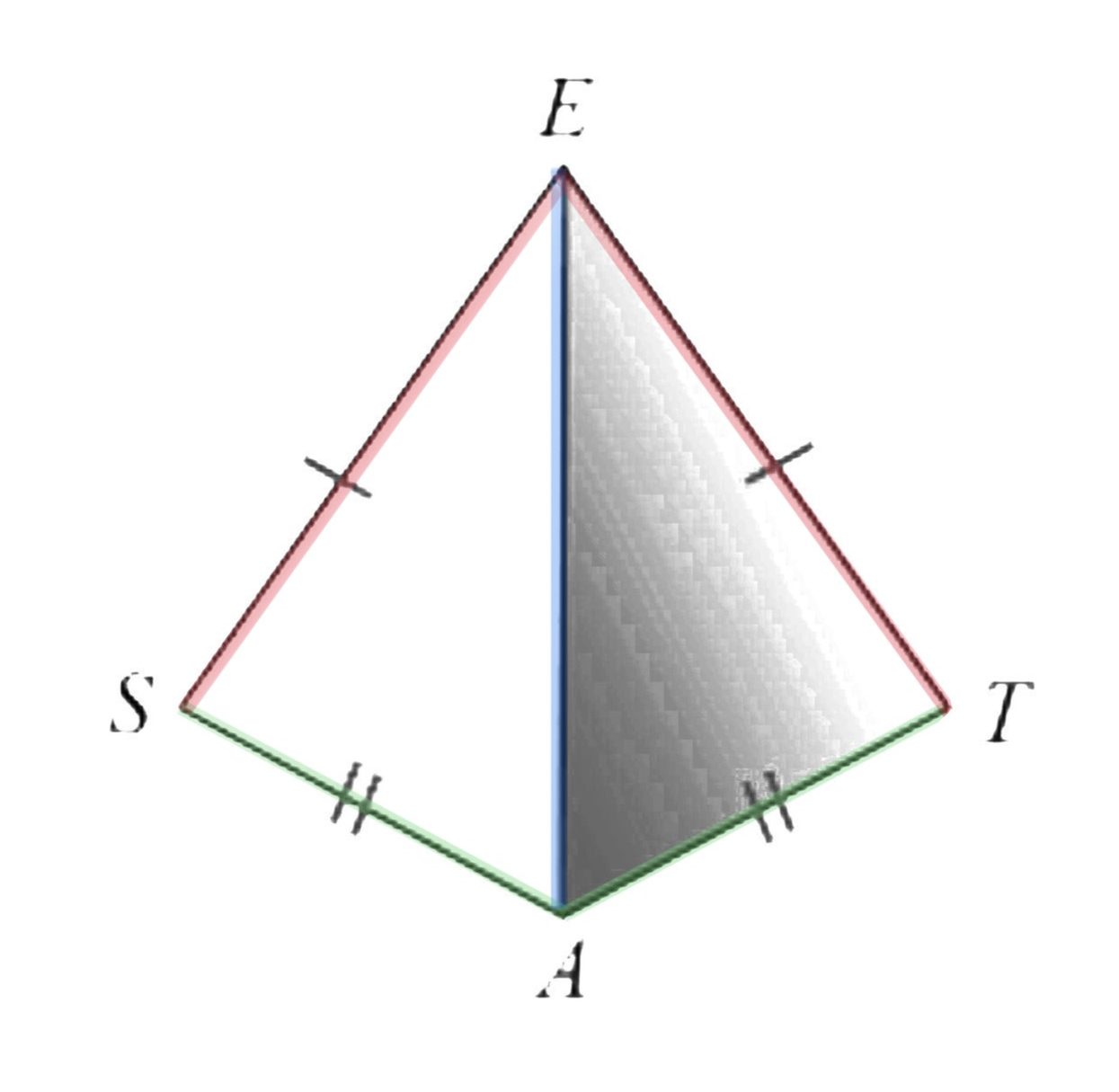
ตัวอย่างที่ 3
จากรูปกำหนดให้ SE = TE และ SA = TA จงพิสูจน์ว่า สามเหลี่ยมSEA และ สามเหลี่ยมTEA เป็นรูปสามเหลี่ยมสองรูปที่เท่ากันทุกประการ