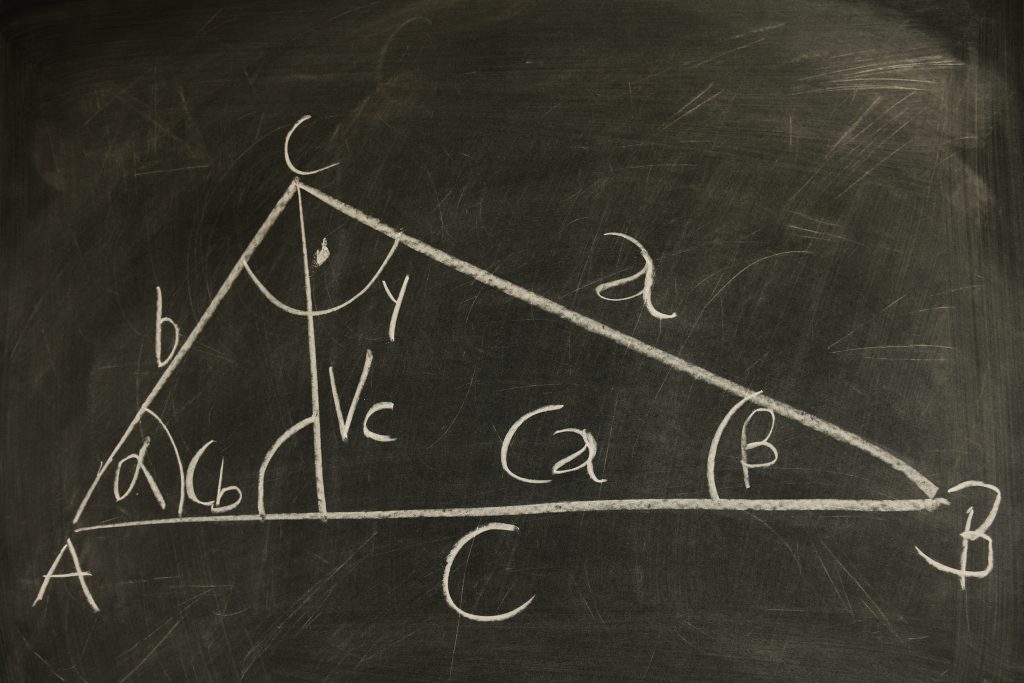ทฤษฎีบทพีทาโกรัส คือ ทฤษฎีความสัมพันธ์ของรูปสามเหลี่ยมมุมฉาก ถือเป็นพื้นฐานในการคำนวณต่าง ๆ ที่มีการประยุกต์ออกไปอย่างกว้างขวาง ซึ่งจำเป็นสำหรับการทำโจทย์ประยุกต์ต่อไป เพราะฉะนั้นจึงควรตั้งใจศึกษาและทำโจทย์ตัวอย่างด้วยการใช้สูตรพีทาโกรัสเป็นประจำ
ทฤษฎีบทพีทาโกรัส
ความสัมพันธ์ของความยาวด้านทั้งสามของรูปสามเหลี่ยมมุมฉากมีความสัมพันธ์กันดังนี้ “ กำลังสองของความยาวของด้านตรงข้ามมุมฉากเท่ากับผลบวกของกำลังสองของความยาวของด้านประกอบมุมฉาก”
ซึ่งความสัมพันธ์ดังกล่าวมีมานานในรูปของทฤษฎีบทพีทาโกรัส ซึ่งเห็นความสัมพันธ์ดังกล่าวในรูปของพื้นที่ดังนี้ “ สำหรับรูปสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านตรงข้ามมุมฉากเท่ากับผลบวกของพื้นที่ของรูปสี่เหลี่ยมจัตุรัสบนด้านประกอบมุมฉาก”
ถ้า สามเหลี่ยม ABC เป็นรูปสามเหลี่ยมมุมฉากที่มี <B เป็นมุมฉาก ความสัมพันธ์ตามทฤษฎีบทพีทาโกรัสมีลักษณะดังรูป
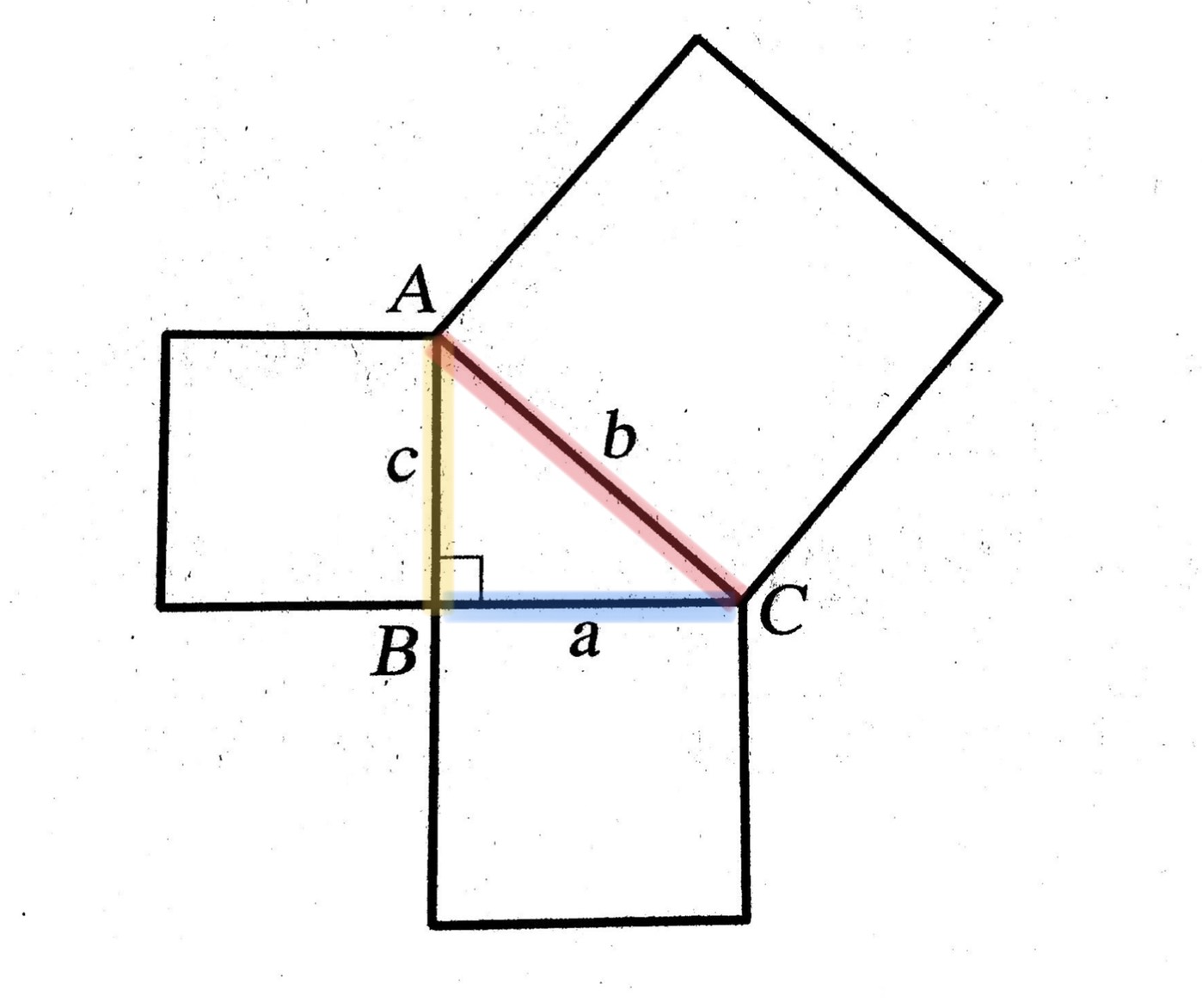

การพิสูจน์ทฤษฎีบทพีทาโกรัส
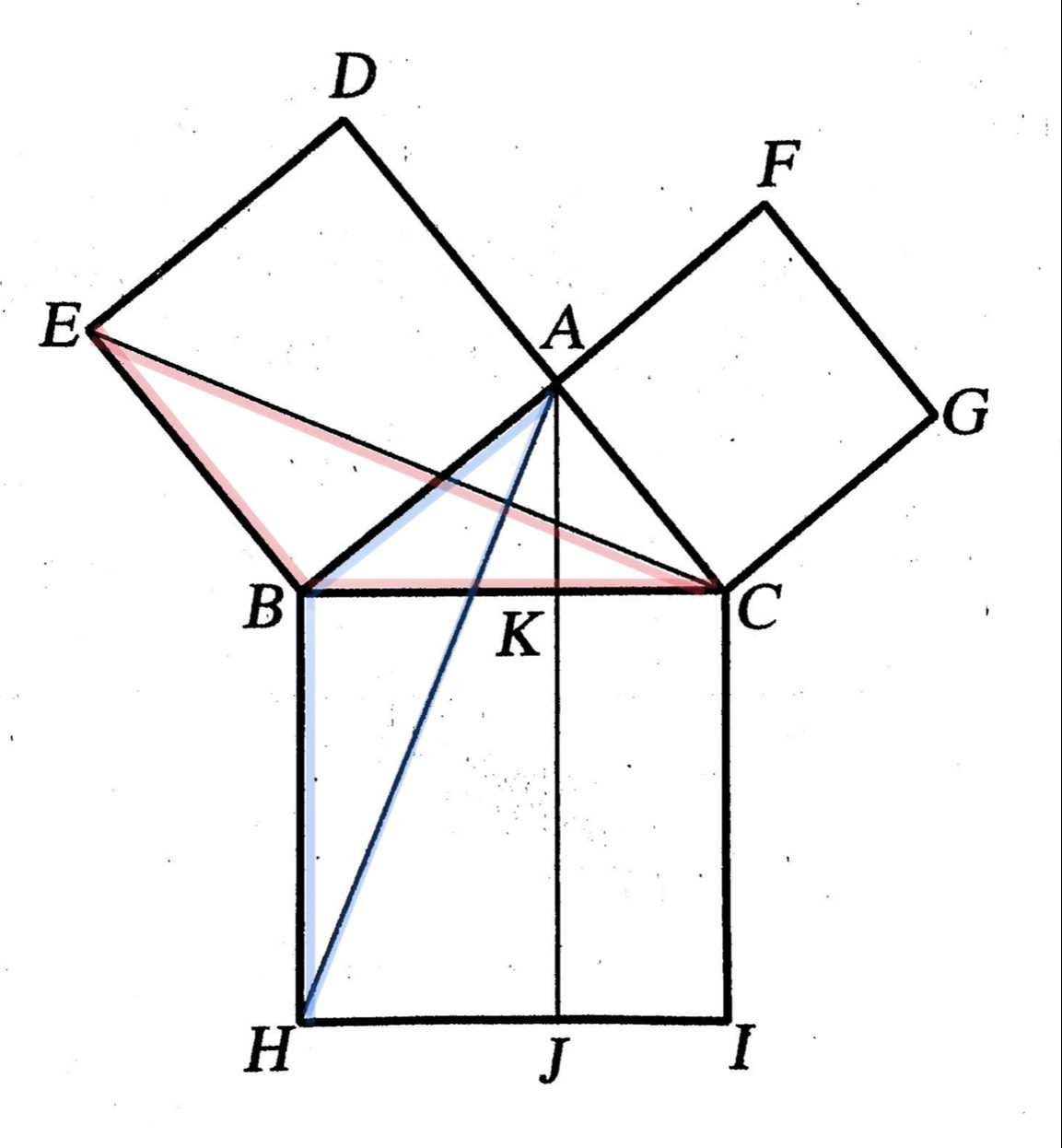
การพิสูจน์ทฤษฎีบทพีทาโกรัสมีได้หลายวิธี และที่จะกล่าวถึงเป็นวิธีการหนึ่งสามารถพิสูจน์ทฤษฎีบทพีทาโกรัสได้การพิสูจน์ สร้างรูปสี่เหลี่ยมจัตุรัส ABED, ACGF และ BCIH บนด้าน AB, AC และ BC ตามลำดับ


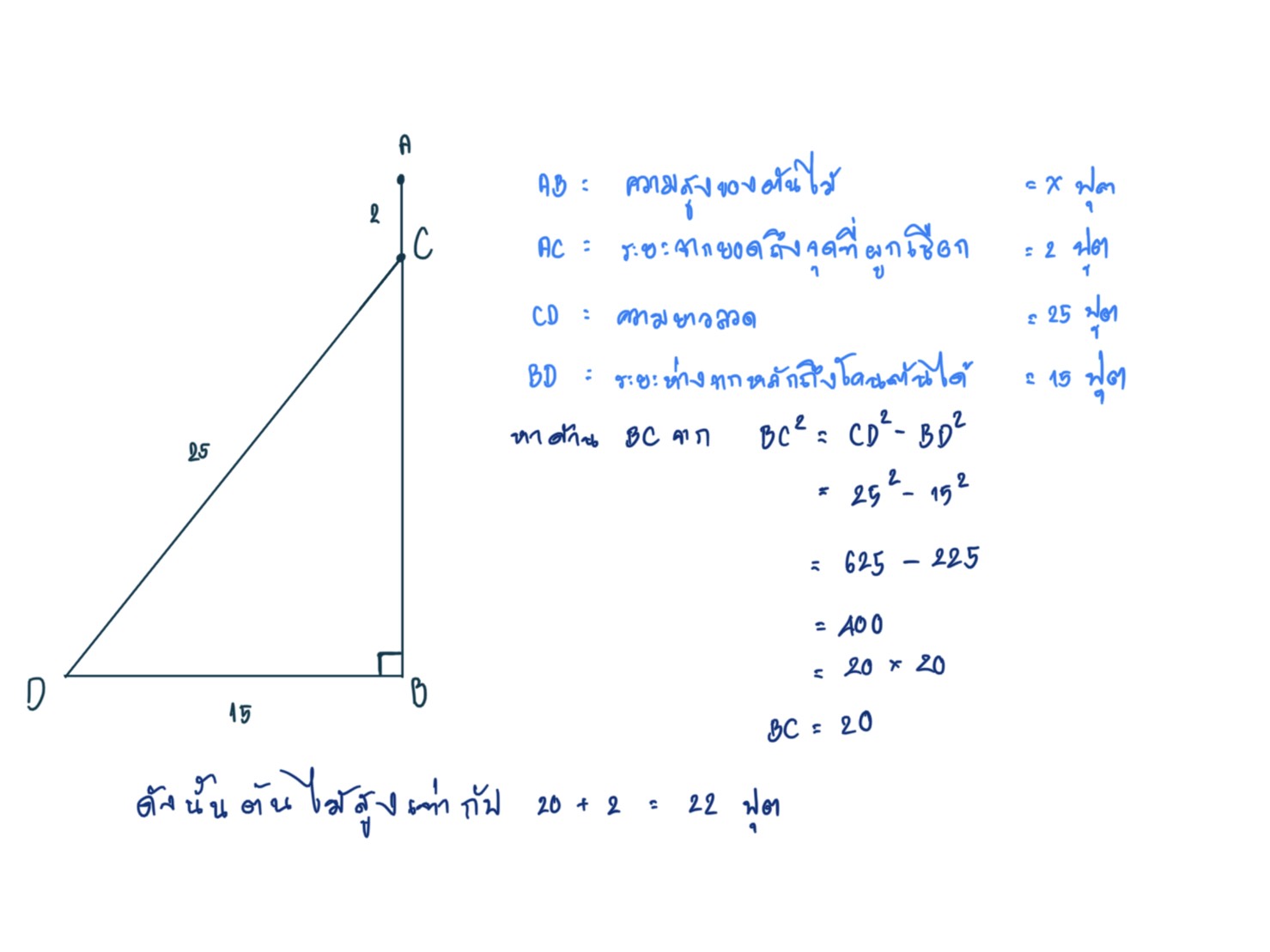
ตัวอย่างที่ 1 ต้นไม้ต้นหนึ่งใช้ลวดผูกที่จุดซึ่งอยู่ห่างจากยอด 2 ฟุต แล้วดึงมาผูกที่หลักซึ่งอยู่ห่างจากโคนต้นไม้ 15 ฟุต ถ้าลวดยาว 25 ฟุต แล้วต้นไม้จะสูงเท่าไร
วิธีทำ ลักษณะของต้นไม้มีลักษณะดังรูป AB
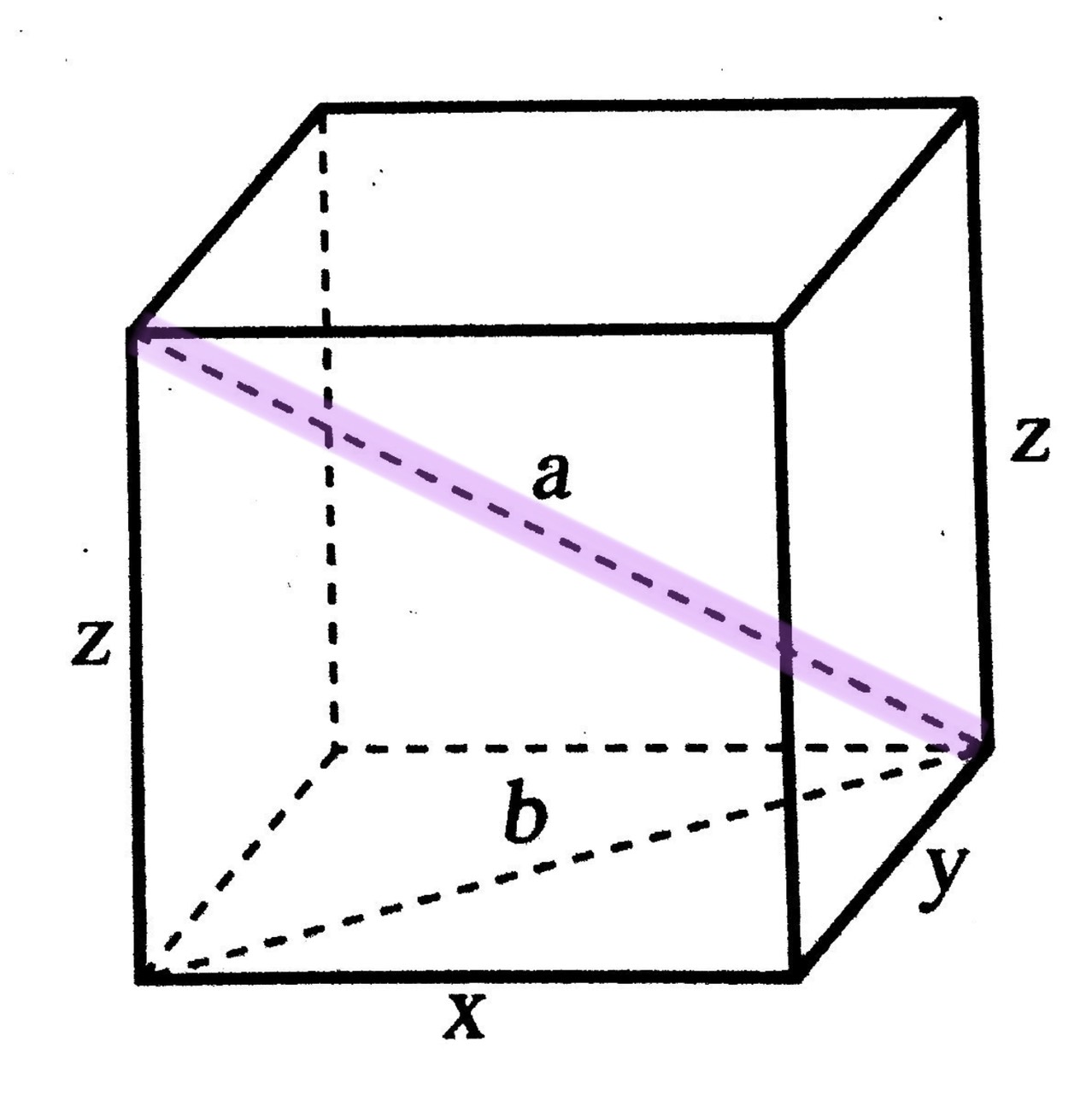
ตัวอย่างที่ 2 ทรงสี่เหลี่ยมมุมฉากขนาดดังรูป มีความยาวของ a เท่ากับเท่าไร
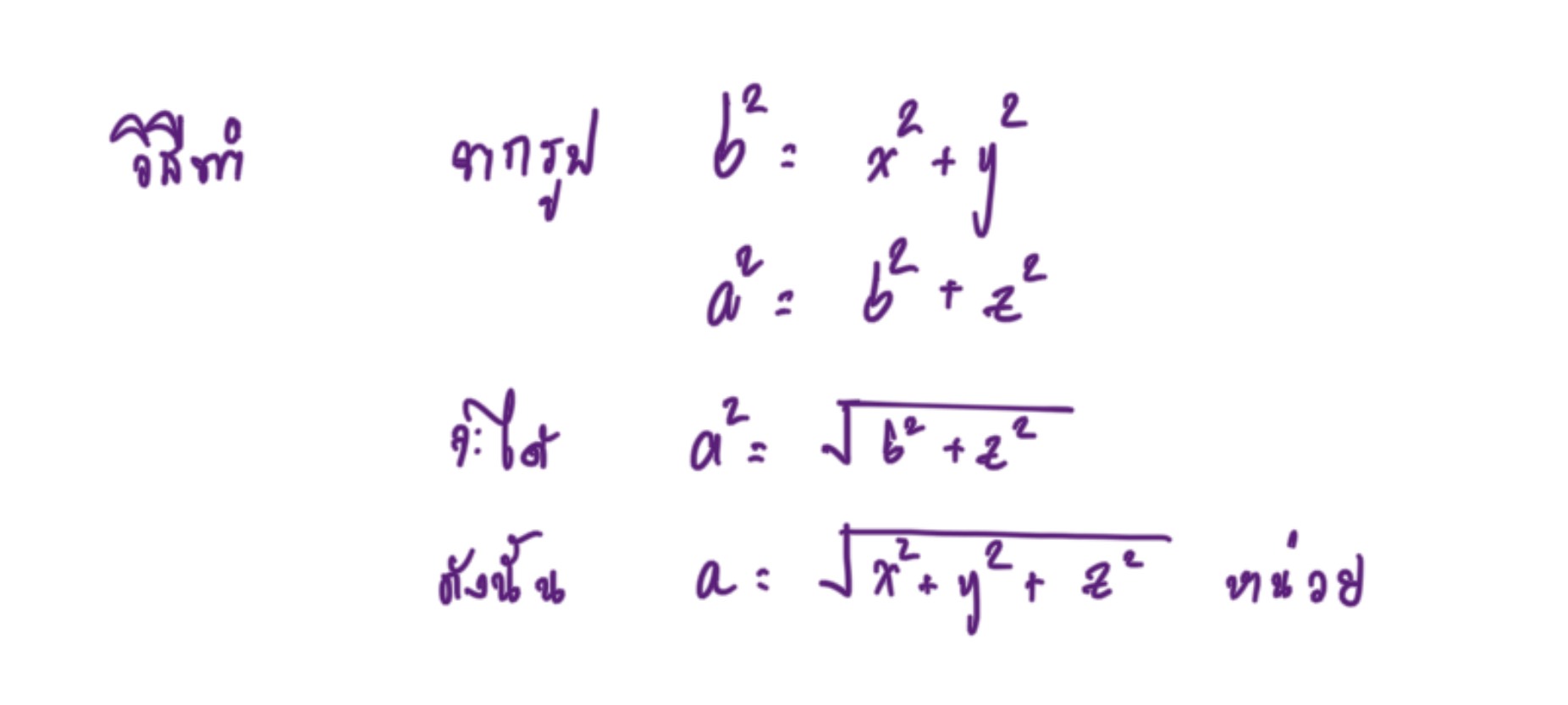
ตัวอย่างที่ 3 จากรูปจงหาระยะ AD ได้เท่าไร
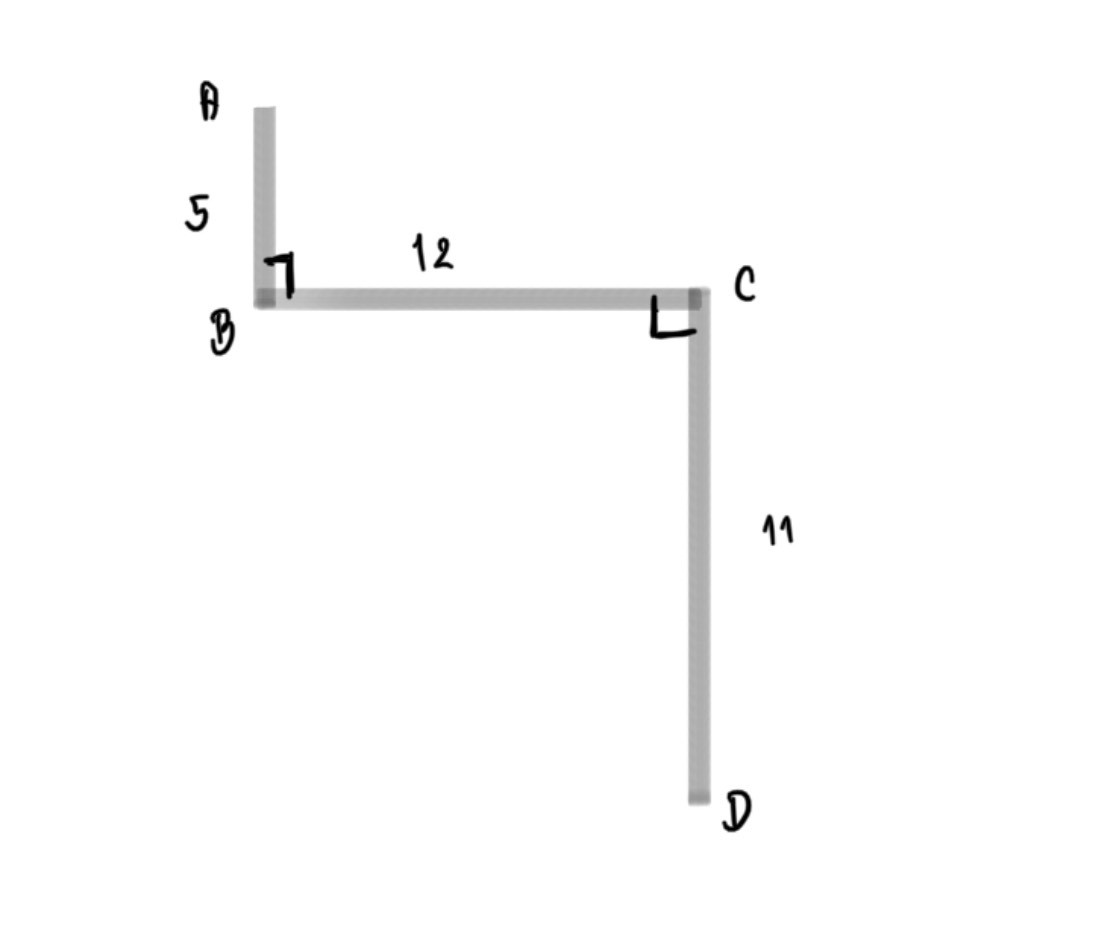
วิธีทำ ต่อเติมรูปให้มีลักษณะเป็นรุปสามเหลี่ยมมุมฉาก
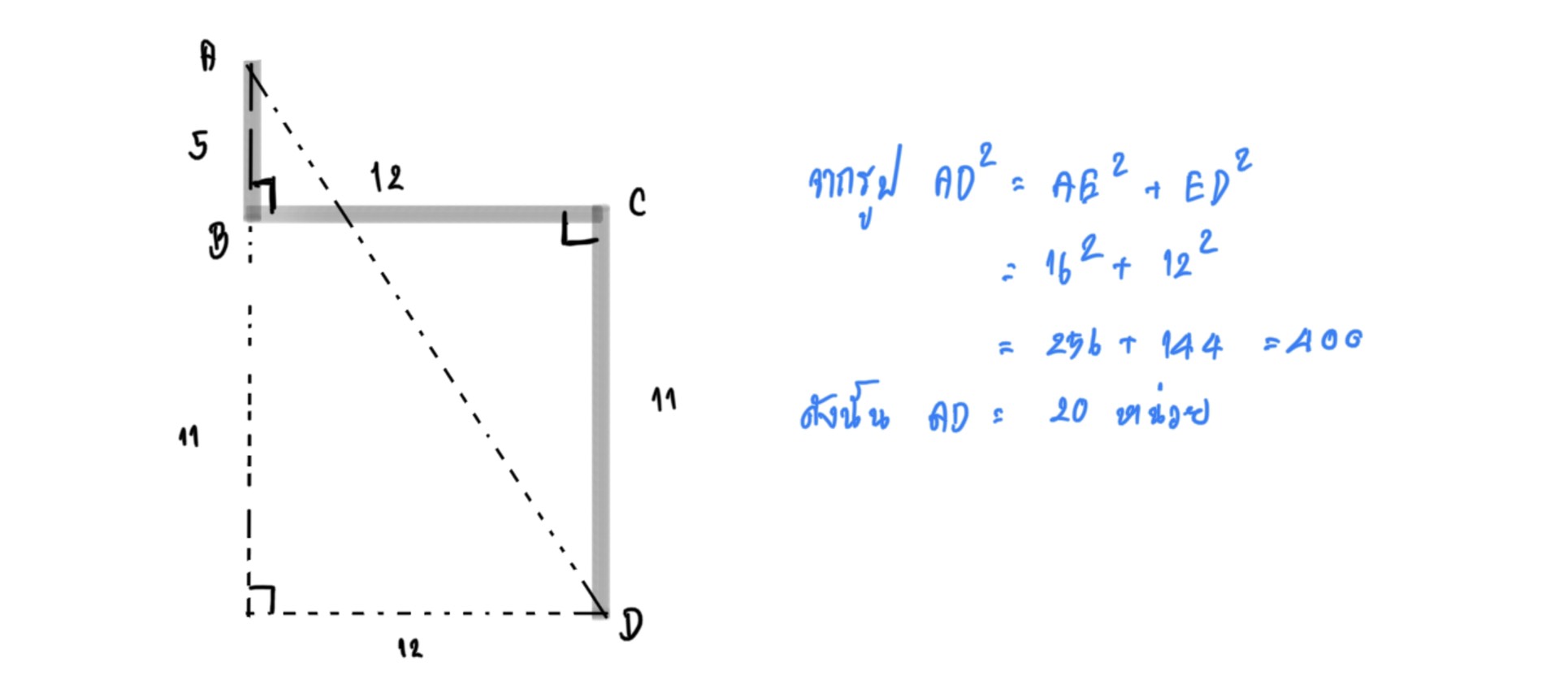
คลิปตัวอย่างเรื่องทฤษฎีบทพีทาโกรัส