ในชีวิตประจำวันนักเรียนมักจะเจอกับโจทย์บวก ลบ ทศนิยมที่ต้องแก้ในชีวิตจริง โดยต้องอาศัยความรู้ทางคณิตศาสตร์ เช่น การซื้อของ การคำนวณระยะทาง รวมไปถึงการชั่งน้ำหนัก เป็นต้น ในบางครั้งตัวเลขที่ได้มักจะออกมาในรูปของทศนิยม ซึ่งก็สอดคล้องกับบทเรียนที่เป็นเรื่องของโจทย์ปัญหาบวกลบทศนิยม บทความนี้จะยกตัวอย่างโจทย์ที่เราอาจจะเจอในชีวิตจริงมาให้น้องๆได้ลองคิดกัน
โจทย์ปัญหาการบวกทศนิยม
ตัวอย่างข้อที่ 1
บ้านของนารีอยู่ห่างจากโรงเรียนเป็นระยะทาง 24.75 กิโลเมตร นารีเดินไปกลับระหว่างบ้านกับโรงเรียนเป็นระยะทางวันละกี่กิโลเมตร
วิเคราะห์โจทย์ ระยะทางจากบ้านไปโรงเรียน เท่ากับ ระยะทางจากโรงเรียนไปบ้าน ดังนั้นเอาระยะทาง 24.75 กิโลเมตรบวกกันสองครั้ง
ประโยคสัญลักษณ์ 24.75+24.75 =________

ตัวอย่างข้อที่ 2
แม่ค้าขายผลไม้วันแรกได้ 17.25 กิโลกรัม วันที่ 2 ขายได้ 26.8 กิโลกรัม รวมทั้งสองวันแม่ค้าขายผลไม้ได้เท่าไหร่
วิเคราะห์โจทย์ โจทย์ต้องการทราบน้ำหนักผลไม้รวมกันทั้งสองวัน ดังนั้นให้นำตัวเลขมาบวกกัน
ประโยคสัญลักษณ์ 17.25 + 26.8 =________

โจทย์ปัญหาการลบทศนิยม
ตัวอย่างข้อที่ 1
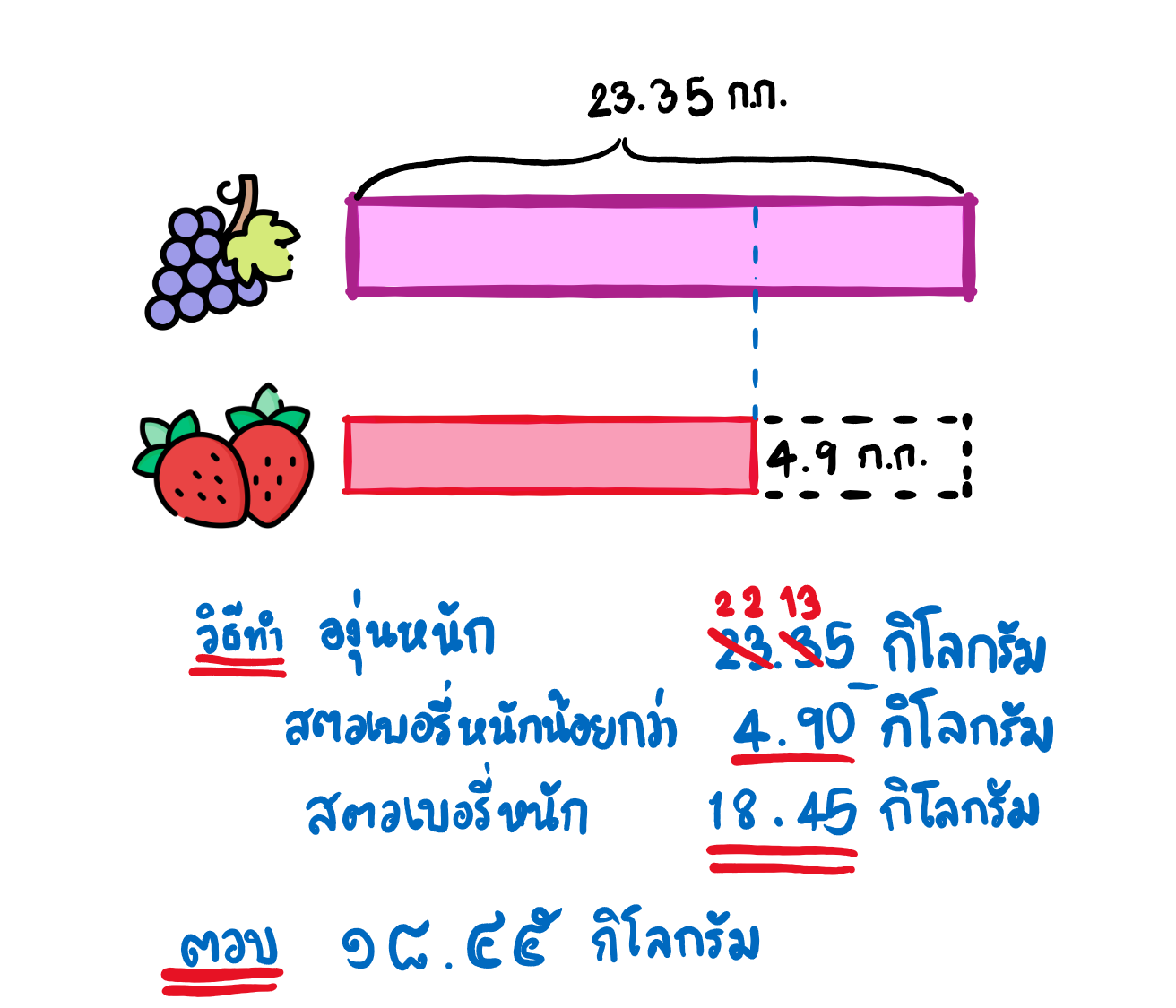
องุ่นถุงหนึ่งหนัก 23.35 กิโลกรัม สตอเบอรี่หนักน้อยกว่าองุ่น 4.9 กิโลกรัม อยากทราบว่าสตอเบอรี่หนักกี่กิโลกรัม
วิเคราะห์โจทย์ โจทย์ต้องการทราบน้ำหนักของสตอเบอรี่ ซึ่งสตอเบอรี่หนักน้อยกว่าองุ่น ดังนั้นนำน้ำหนักขององุ่นหักน้ำหนักที่น้อยกว่าออกก็จะได้เป็นน้ำหนักที่แท้จริงของสตอเบอรี่
ประโยคสัญลักษณ์ 23.35 – 4.9 =________
ตัวอย่างข้อที่ 2
แม่ซื้อทุเรียนที่ตลาดมีน้ำหนัก 2.75 กิโลกรัม พ่อซื้อส้มโอมีน้ำหนัก 1.8 กิโลกรัม ทุกเรียนที่แม่ซื้อมามีน้ำหนักมากกว่าส้มโอที่พ่อซื้อมากี่กิโลกรัม
วิเคราะห์โจทย์ โจทย์อยากทราบส่วนต่างที่มากกว่าของผลไม้สองชนิดที่ซื้อมา ดังนั้นนำน้ำหนักของผลไม้ 2 ชนิดมาลบกัน
ประโยคสัญลักษณ์ 2.75 – 1.8 =________