สาระสำคัญของการเปรียบเทียบเศษส่วนและจำนวนคละนั้นอยู่ที่การทำตัวส่วนให้เท่ากัน หากเศษส่วนที่นำมาเปรียบเทียบมีตัวส่วนที่เท่ากันอยู่แล้วก็จะง่ายต่อการบอกได้ว่าเศษส่วนไหนมีค่ามากกว่าหรือเศษส่วนไหนมีค่าน้อยกว่า บทความนี้จึงจะแยกประเภทของการเปรียบเทียบเศษส่วนให้ดังนี้
การเปรียบเทียบเศษส่วนและจำนวนคละ
ประเภทของการเปรียบเทียบเศษส่วน
1.การเปรียบเทียบเศษส่วนที่ตัวส่วนเท่ากันและจำนวนคละ
“ส่วนเท่ากัน เศษมากจะมีค่ามากกว่า” ความหมายก็คือ กรณีที่เปรียบเทียบเศษส่วนที่มีตัวส่วนเท่ากัน ถ้าเศษมากกว่า เศษส่วนนั้นก็จะมีค่ามากกว่ายกตัวอย่างภาพข้างล่าง
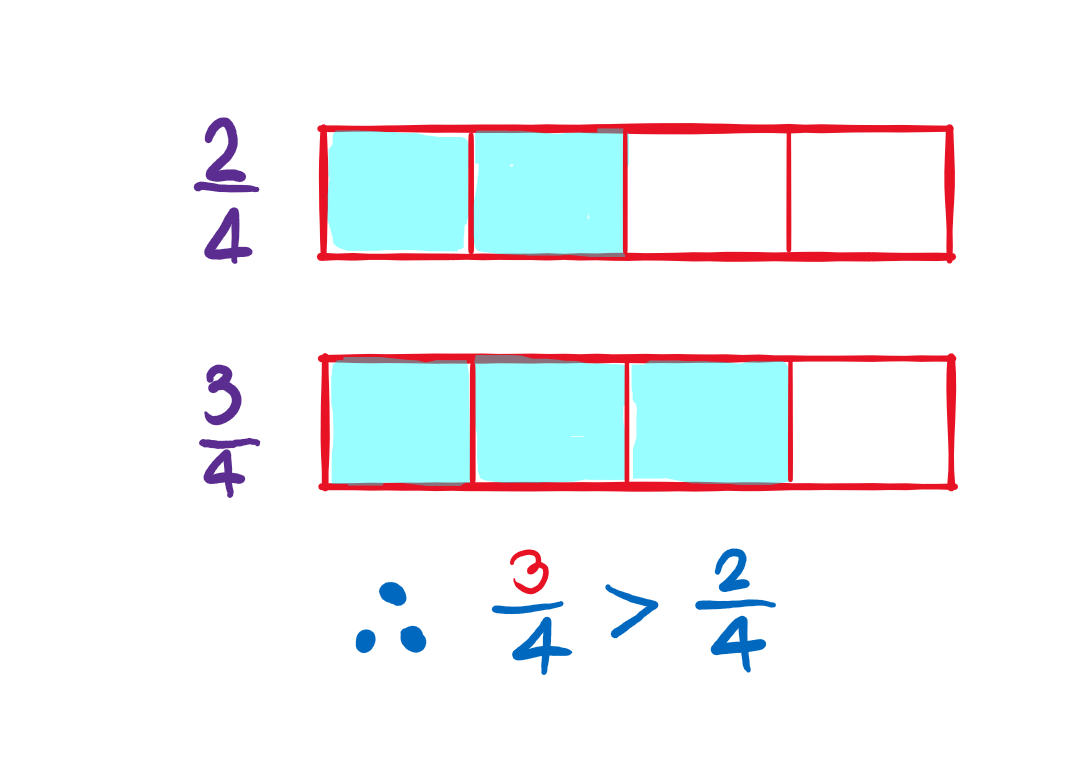
เปรียบเทียบเศษส่วนจำนวนคละกับเศษส่วนจำนวนคละที่ตัวส่วนเท่ากัน “จำนวนเต็มมาก่อนเศษส่วนมาหลัง” ความหมายก็คือ เมื่อเปรียบเทียบจำนวนคละสองจำนวน จำนวนคละที่มีจำนวนเต็มมากกว่าจะมีค่ามากกว่าเสมอ แต่ถ้าจำนวนเต็มมีค่าเท่ากันเราจึงพิจารณาเศษส่วนเป็นลำดับถัดไปตัวอย่างภาพข้างล่าง
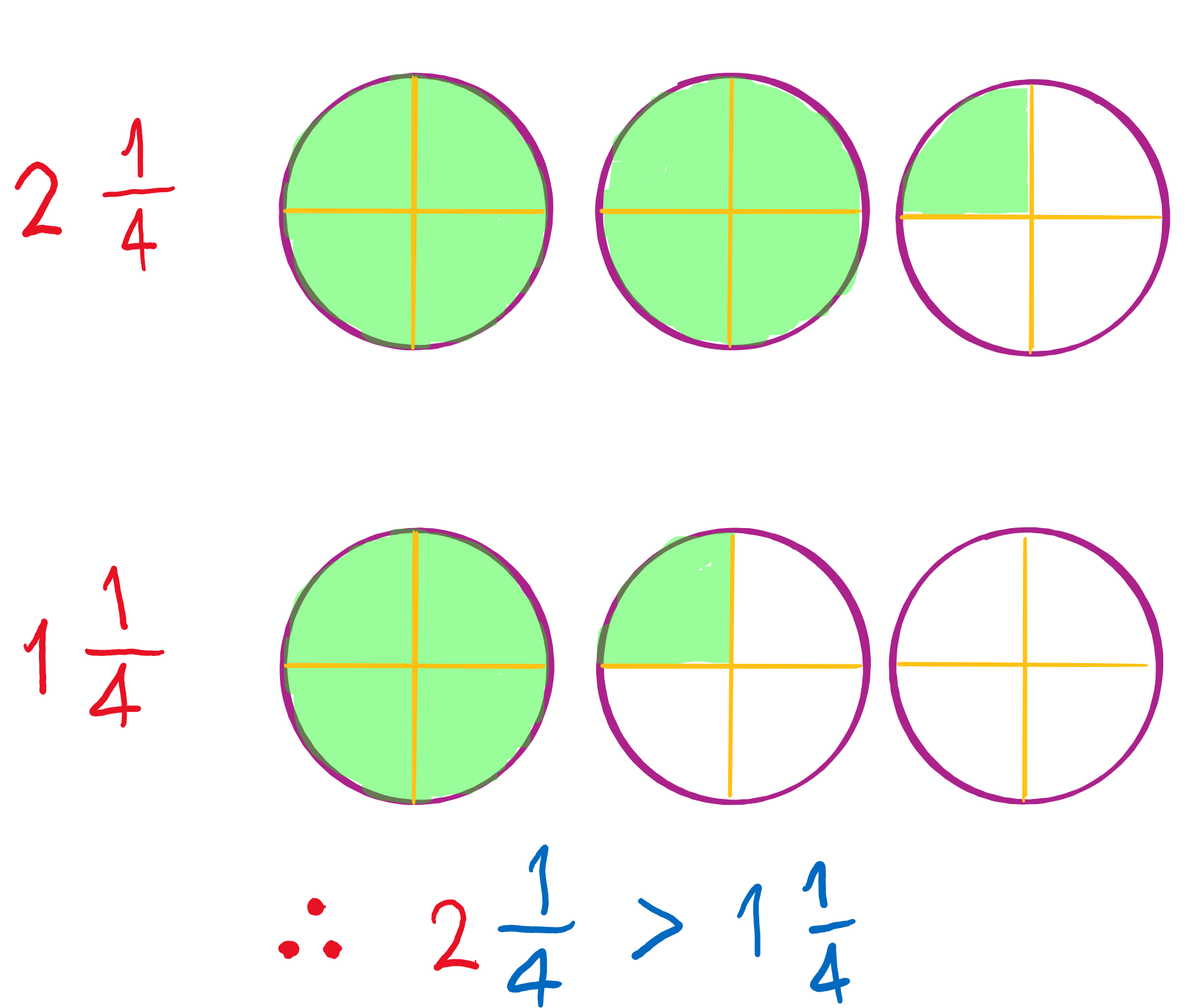
จำนวนเต็มไม่เท่ากัน
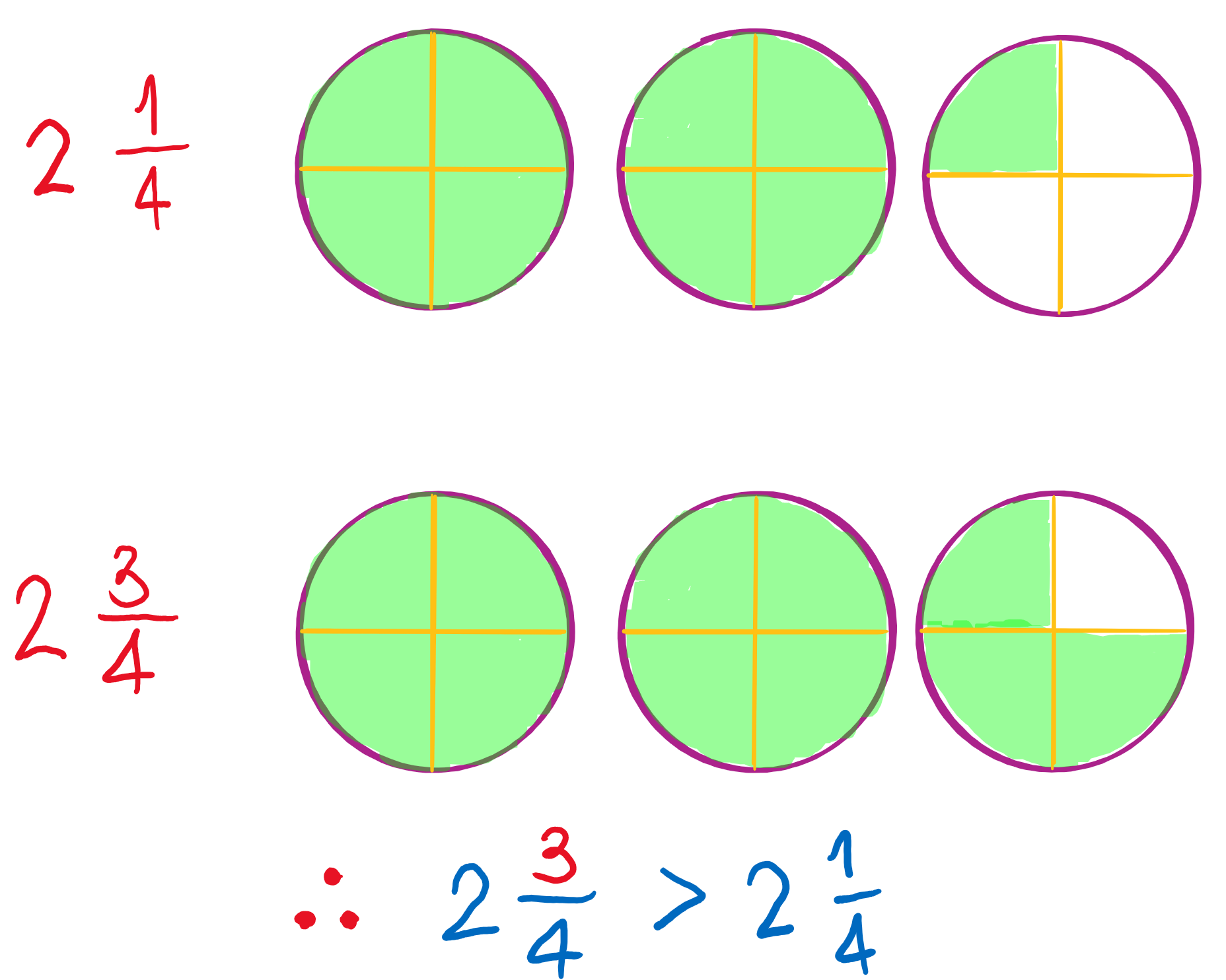
จำนวนเต็มเท่ากัน
2.การเปรียบเทียบเศษส่วนที่ตัวเศษเท่ากันและจำนวนคละ
“เศษเท่ากัน ส่วนจะมีค่าสวนทาง” ความหมายก็คือ กรณีที่เปรียบเทียบเศษส่วนที่มีตัวเศษเท่ากัน ตัวส่วนจะมีค่าสวนทางก็คือยิ่งส่วนมากเศษส่วนนั้นก็จะมีค่าน้อยยกตัวอย่างภาพข้างล่าง
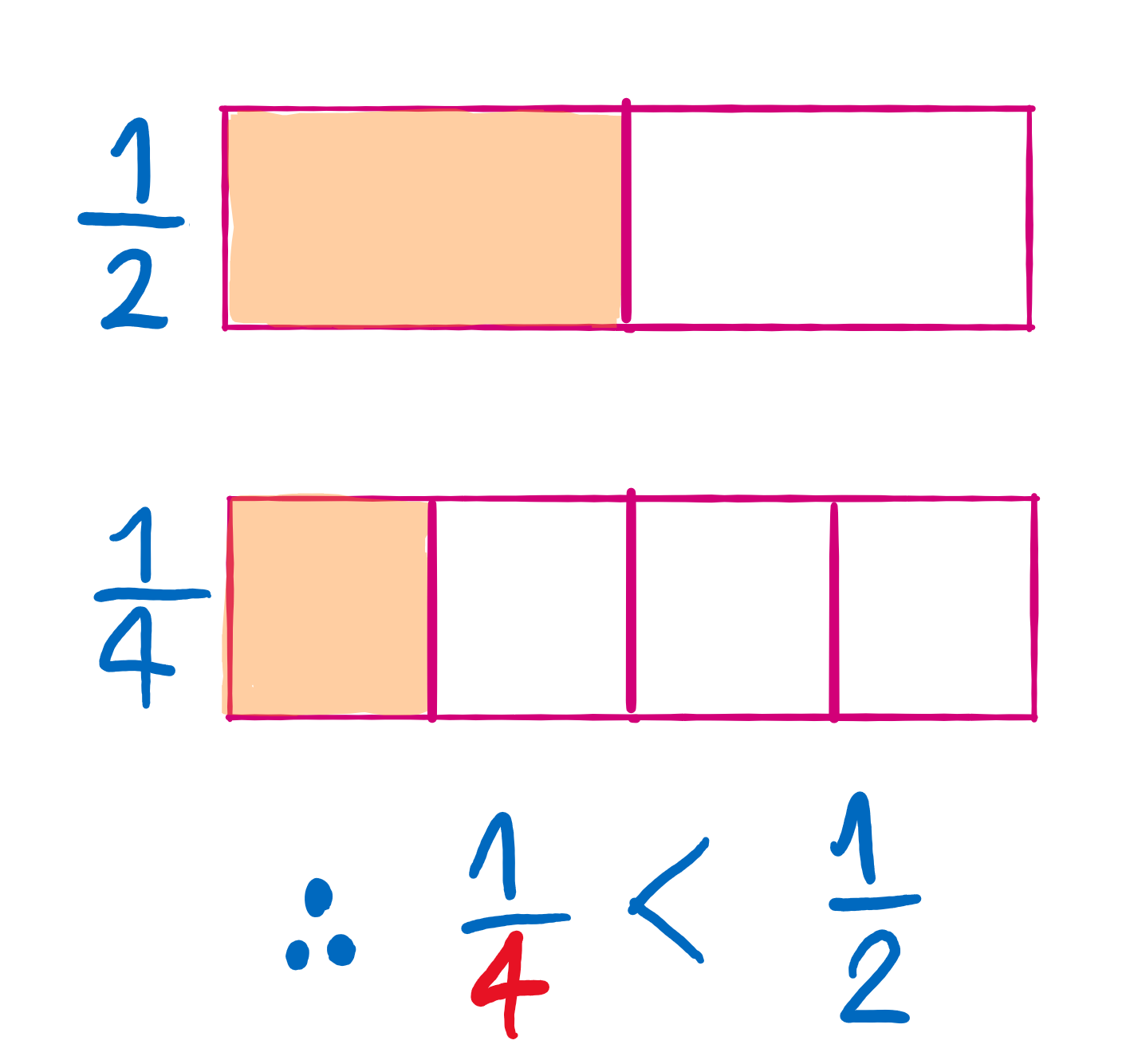
เปรียบเทียบเศษส่วนจำนวนคละกับเศษส่วนจำนวนคละที่ตัวเศษเท่ากัน ทำเช่นเดียวกับกรณีที่เปรียบเทียบจำนวนคละที่มีตัวส่วนเท่ากัน ก็คือให้พิจารณาจำนวนเต็มก่อนแล้วจึงพิจารณาเศษส่วน
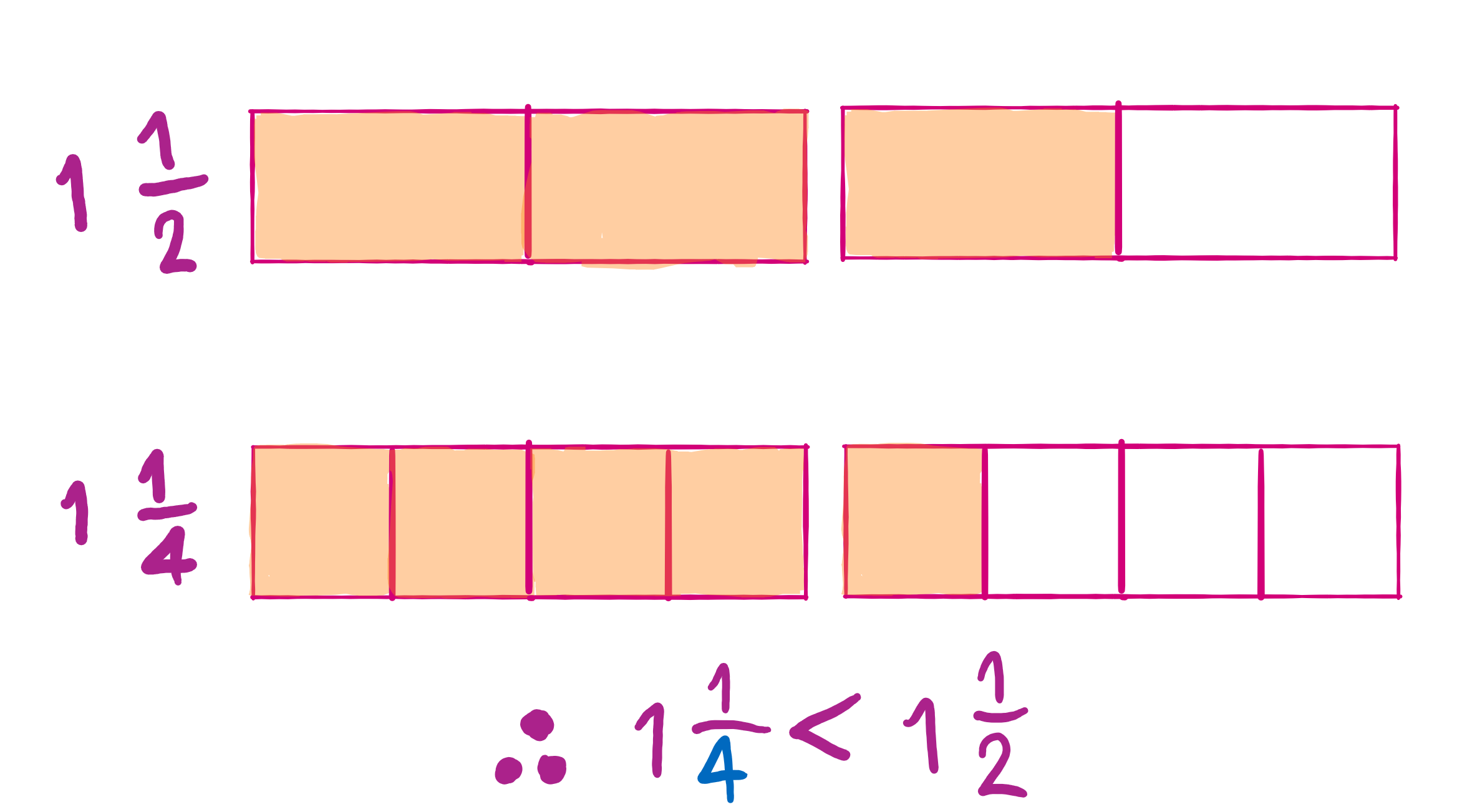
จำนวนเต็มเท่ากัน
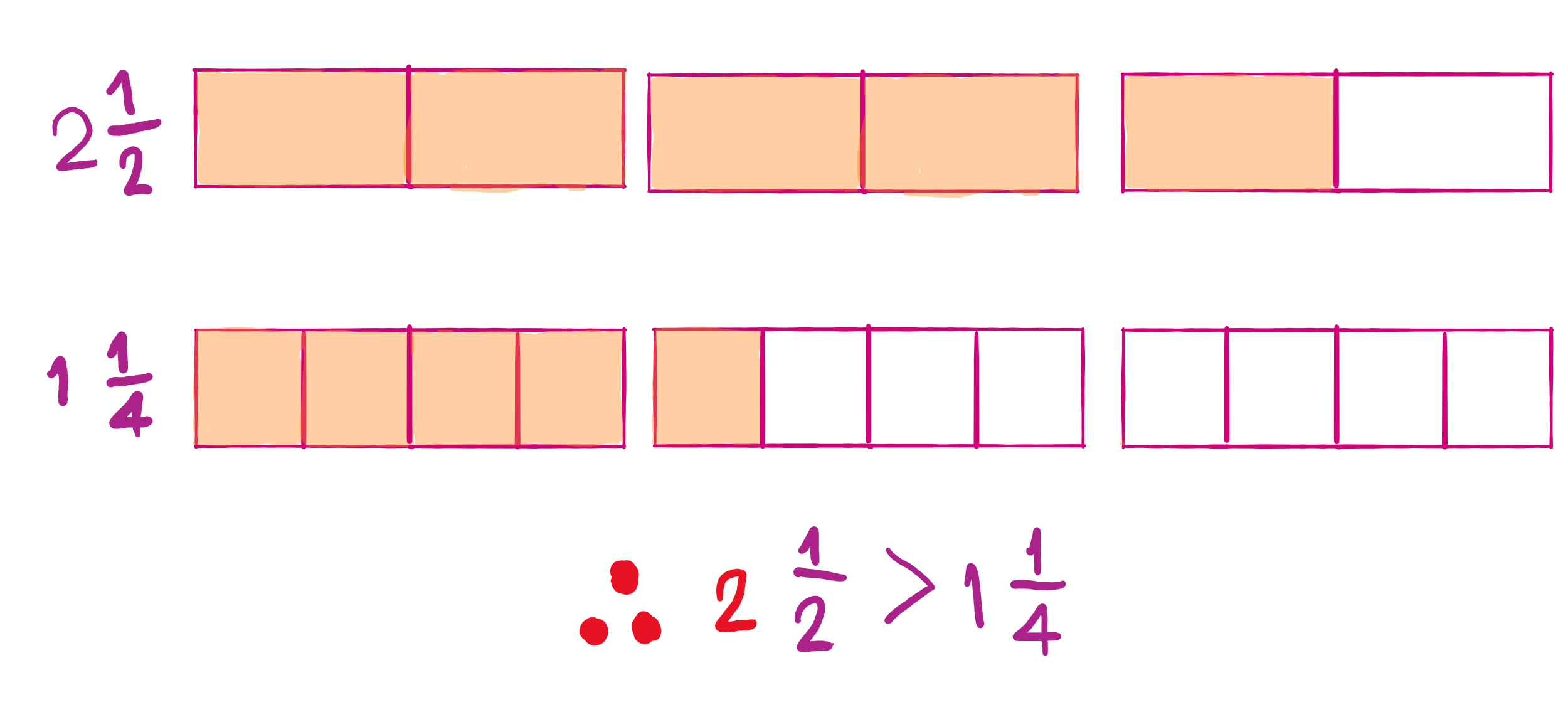
จำนวนเต็มไม่เท่ากัน
3.การเปรียบเทียบเศษส่วนที่ไม่เท่ากันและจำนวนคละ
“ตัวส่วนเท่ากันถึงจะเปรียบเทียบกันได้” ความหมายก็คือ กรณีที่เปรียบเทียบเศษส่วนที่ไม่เท่ากัน ต้องทำให้ตัวส่วนของเศษส่วนทั้งสองจำนวนเท่ากันก่อนเหมือนกับหัวข้อที่ 1 ข้างต้น
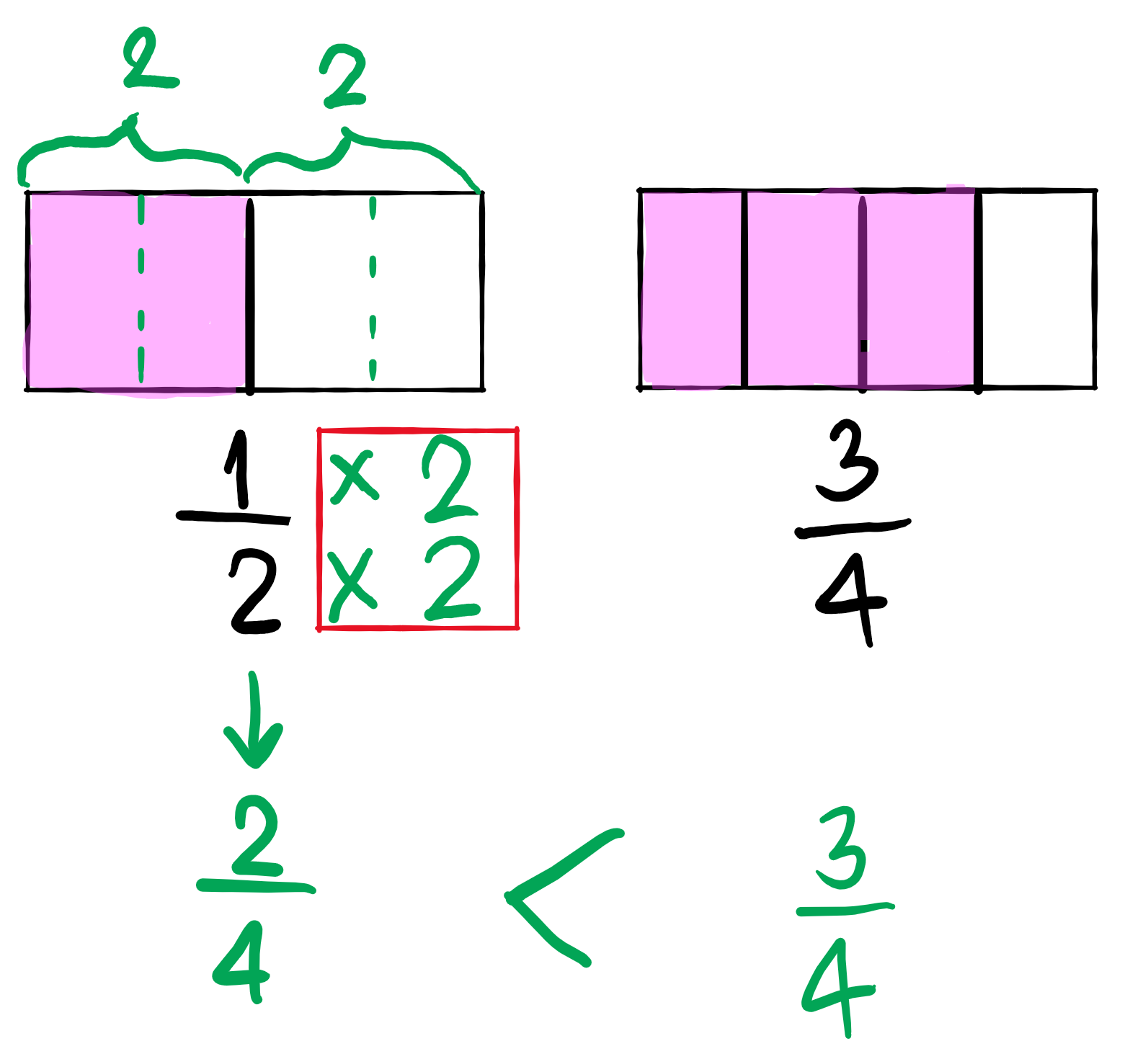
เปรียบเทียบเศษส่วนจำนวนคละกับเศษส่วนจำนวนคละที่เศษส่วนไม่เท่ากัน ยกตัวอย่างเช่น
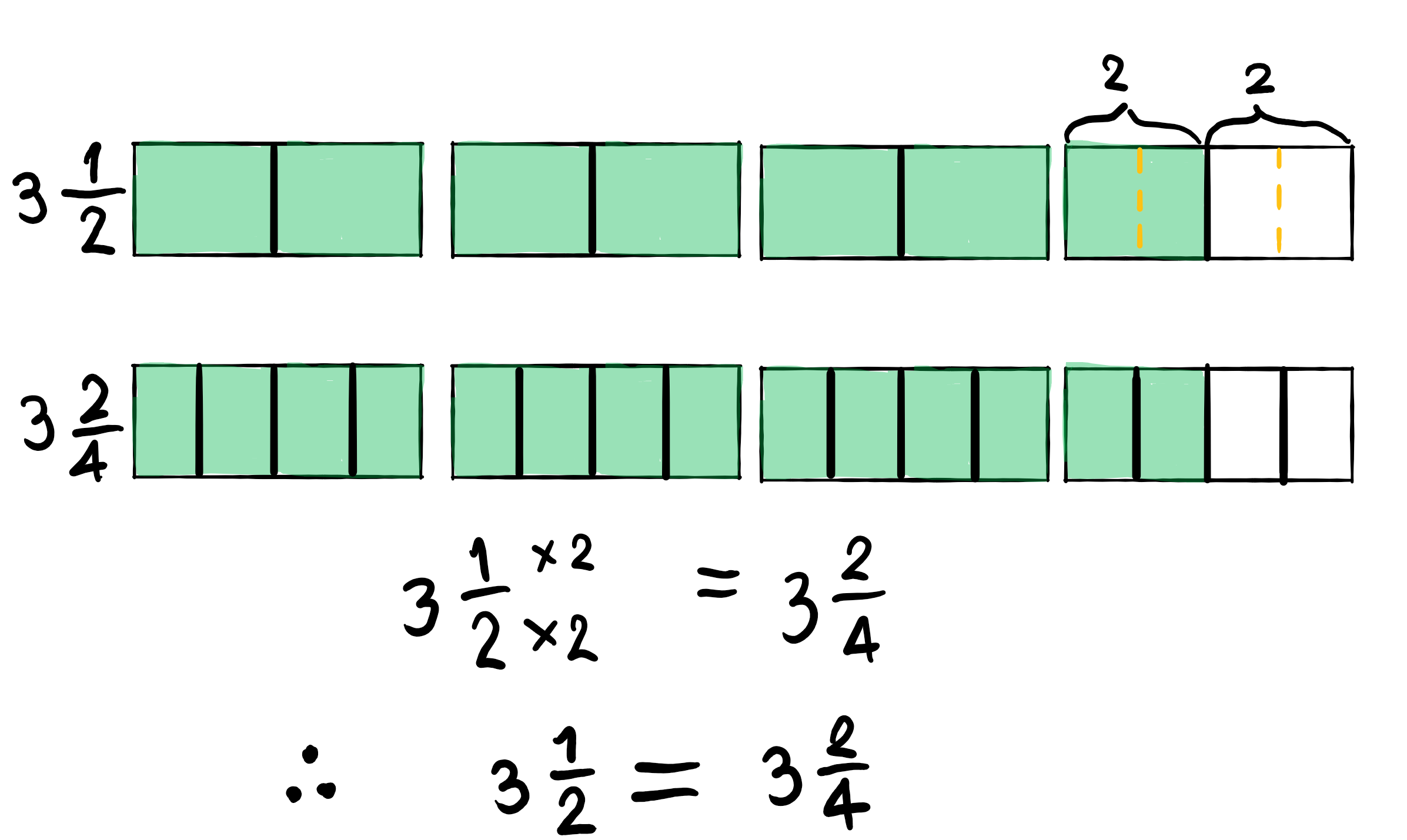
4.การเปรียบเทียบเศษเกินกับจำนวนคละ
ทำได้สองวิธีคือ “เปลี่ยนเศษเกินเป็นจำนวนคละ” แล้วใช้หลักการเปรียบเทียบจำนวนคละกับจำนวนคละ และ “เปลี่ยนจำนวนคละเป็นเศษเกิน” แล้วใช้หลักการเปรียบเทียบเศษส่วนกับเศษส่วน ยกตัวอย่างทั้งสองวิธีตามภาพข้างล่าง
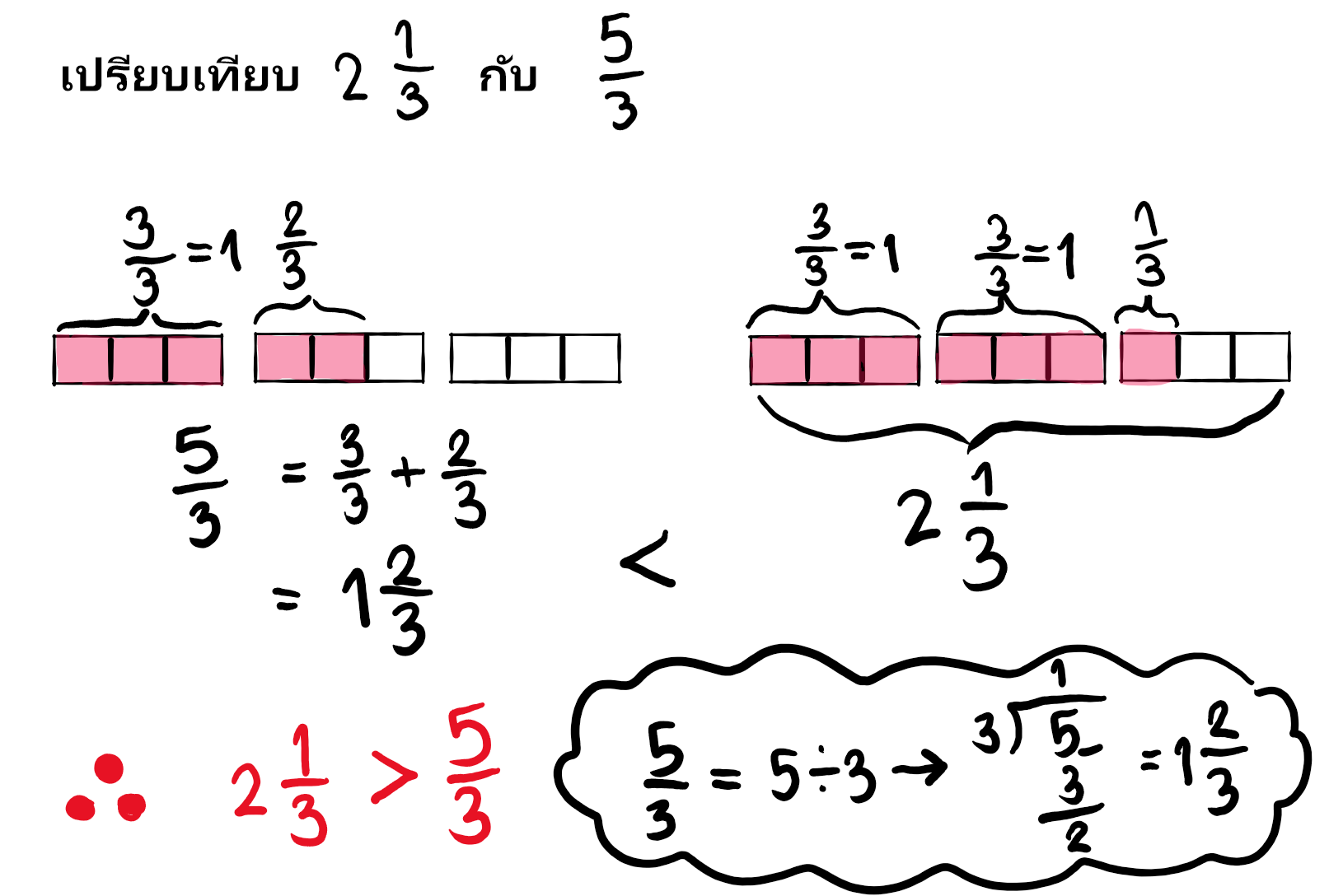
วิธีที่ 1 “เปลี่ยนเศษเกินเป็นจำนวนคละ”
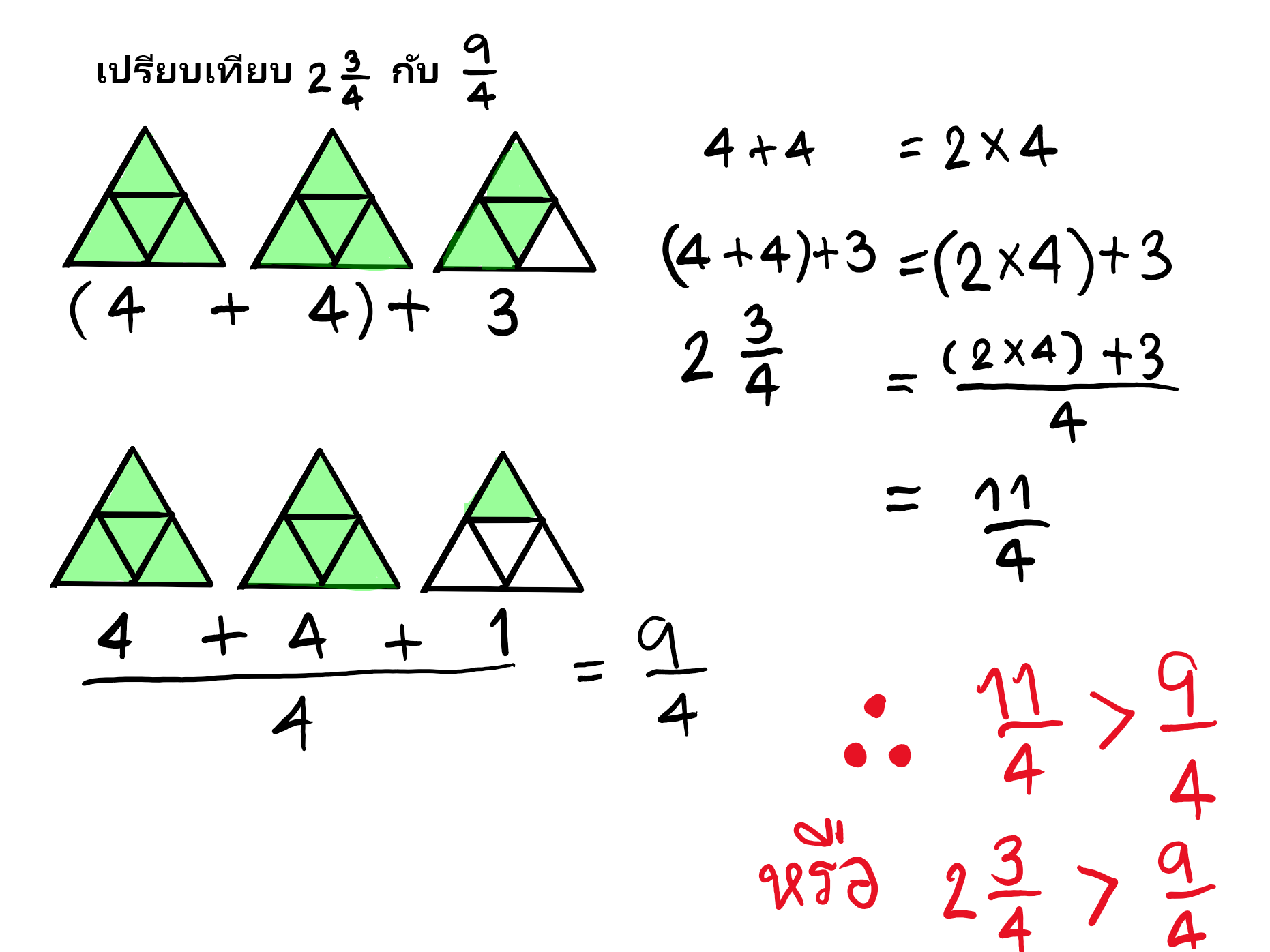
วิธีที่ 2 ”เปลี่ยนจำนวนคละเป็นเศษเกิน”
สรุปเนื้อหาการเปรียบเทียบเศษส่วนมีทั้งหมด 4 ประเภทตามบทความข้างต้น และตัวอย่างที่ได้ยกมาสามารถนำไปแก้โจทย์ในเรื่องการเปรียบเทียบเศษส่วนได้อย่างเข้าใจและทำแบบฝึกหัดได้อย่างถูกต้อง ครั้งหน้ามีบทความเกี่ยวกับคณิตศาสตร์ที่จะพาน้อง ๆ เข้าใจหลักการต่าง ๆได้ดียิ่งขึ้น หวังว่าจะชอบและติดตามกันต่อไปนะคะ


















