“สมมูลและนิเสธ” ของประโยคที่มีตัวบ่งปริมาณ

สมมูลและนิเสธ เราเคยเรียนกันไปแล้วก่อนหน้านี้ แต่เป็นของประพจน์ p, q, r แต่ในบทความนี้จะเป็นสมมูลและนิเสธของประโยคที่มีตัวบ่งปริมาณ ซึ่งก็จะเอาเนื้อหาก่อนหน้ามาปรับใช้กับประโยคที่มีตัวบ่งปริมาณ สิ่งที่เราจะต้องรู้และจำให้ได้ก็คือ การสมมูลกันของประพจน์ เพราะจะได้ใช้ในบทนี้แน่นอนน ใครที่ยังไม่แม่นสามารถไปอ่านได้ที่ บทความรูปแบบของประพจน์ที่สมมูลกัน 

นิเสธของตัวบ่งปริมาณ

เมื่อเราเติมนิเสธลงไปในประโยคที่มีตัวบ่งปริมาณ ข้อความต่อไปนี้จะสมมูลกัน

กรณี 1 ตัวแปร

∼∀x[P(x)] ≡ ∃x[∼P(x)]

∼∃x[P(x)] ≡ ∀x[∼P(x)]

กรณี 2 ตัวแปร

∼[∀x∃x [P(x, y)]] ≡ ∃x∀x[∼P(x, y)]

∼[∃x∀x[P(x, y)]] ≡ ∀x∃x [∼P(x, y)]

∼[∃x∃x[P(x, y)]] ≡ ∀x∀x [∼P(x, y)]

∼[∀x∀x [P(x, y)]] ≡ ∃x∃x[∼P(x, y)]

**การเติมนิเสธลงไปในประโยคที่มีตัวบ่งปริมาณเอกภพสัมพัทธ์จะยังคงเดิม เช่น ถ้าเอกภพสัมพัทธ์เป็น เมื่อเติมนิเสธลงไป เอกภพสัมพัทธ์ก็ยังเป็น เหมือนเดิม

ข้อสังเกต จะเห็นว่าเมื่อเติมนิเสธลงไป สิ่งที่เปลี่ยนไปคือตัวบ่งปริมาณ เช่น ถ้าตอนแรกเป็น ∀ เติมนิเสธไปจะกลายเป็น ∃ และเครื่องหมาย ∼ จากที่อยู่หน้าตัวบ่งปริมาณก็จะไปอยู่หน้า P(x) แทน

**แล้วถ้าหน้า P(x) มีเครื่องหมาย ∼ อยู่แล้วล่ะ??

เรามาดูตัวอย่างกัน  ∼∃x[∼ P(x)] ≡ ∀x[∼(∼ P(x))] ≡ ∀x[ P(x)]

จะเห็นว่าตัวอย่างข้างต้นก็เหมือนประพจน์ทั่วไปค่ะ เช่น ∼(∼p) ≡ p เห็นไหมคะว่าไม่ต่างกันเลยแค่มีตัวบ่งปริมาณเพิ่มมา

จากที่เรารู้จักนิเสธแล้วเรามาทำตัวอย่างกันเลยค่ะ

ตัวอย่าง “สมมูลและนิเสธ” ของตัวบ่งปริมาณ

1.) นิเสธของข้อความ ∀x∃y[(xy = 0 ∧ x ≠ 0 ) → y = 0] สมมูลกับข้อความ ∃x∀y[( xy = 0 ∧ x ≠ 0) ∧ y ≠ 0]

สรุปได้ว่า ข้อความทั้งสองสมมูลกัน

**เราสมมติ p q r เพื่อให้มองได้ง่ายขึ้นไม่สับสน

2.) นิเสธของข้อความ ∃x∀y[xy < 0 → (x < 0 ∨ y < 0)] คือ

∀x∃y[(xy < 0) ∧(x ≥ 0 ∧ y ≥ 0)] 

วิธีตรวจสอบ

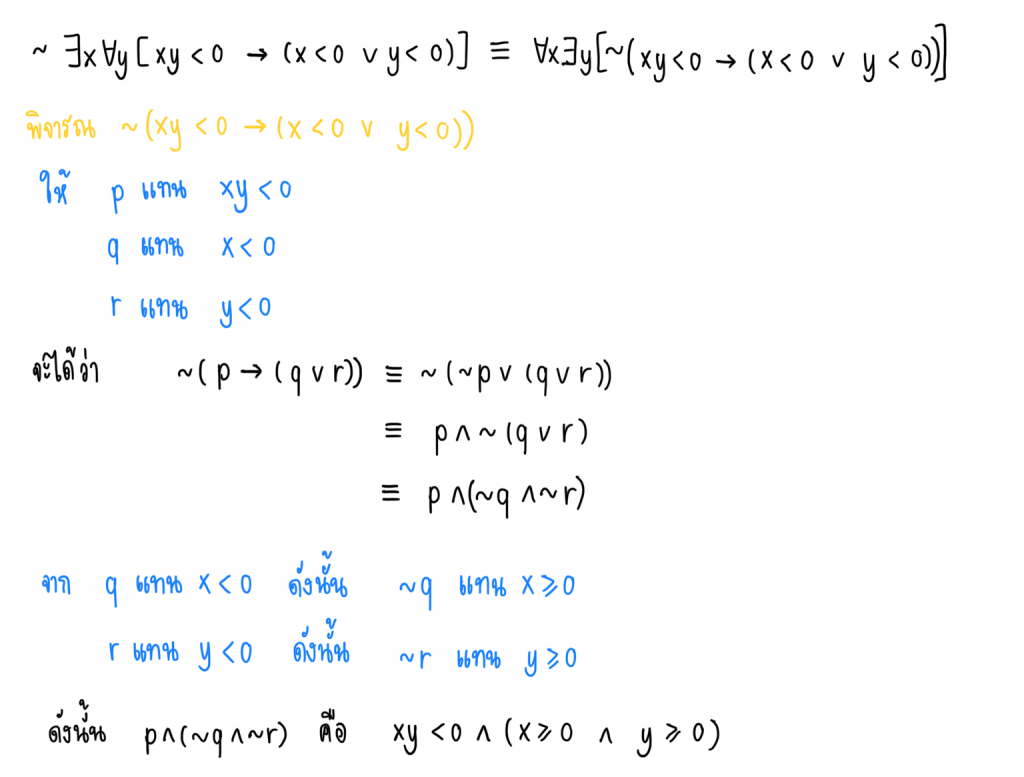
ดังนั้น ข้อความข้างต้นเป็นจริง

3.) นิเสธของข้อความ ∃x[(∼P(x)) ∧ Q(x) ∧ (∼R(x))] คือข้อความ ∀x[Q(x) → (P(x) ∨ R(x))]

วิธีตรวจสอบ

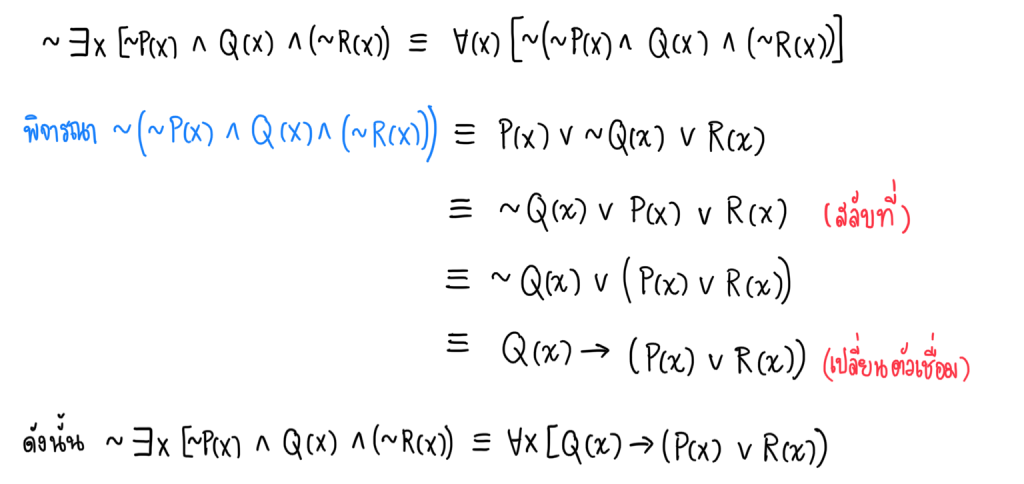
สรุป

สมมูลและนิเสธในบทความนี้จะคล้ายๆกับรูปแบบการสมมูลของประพจน์ที่เราเคยเรียนก่อนหน้า แค่เพิ่มตัวบ่งปริมาณเข้าไป วิธีการตรวจสอบว่าเป็นนิเสธหรือไม่เราก็จะเอาการสมมูลของประพจน์เข้ามาช่วยแค่นั้นเอง