ในชีวิตประจำวันมความจำเป็นในการใช้จำนวนตัวเลขต่างๆ ซึ่งเกิดปัญหาขึ้นมากมายเมื่อนำจำนวนบางคู่มาลบกัน หารกัน แล้วกระทำไม่ได้ จึงคิดค้นหลักการจำนวนตรรกยะ นี้ทำให้ปัญหาที่เกิดขึ้นหายไป เช่น ช่วยแก้ปัญหาการหาคำตอบของสมการ เป็นต้น
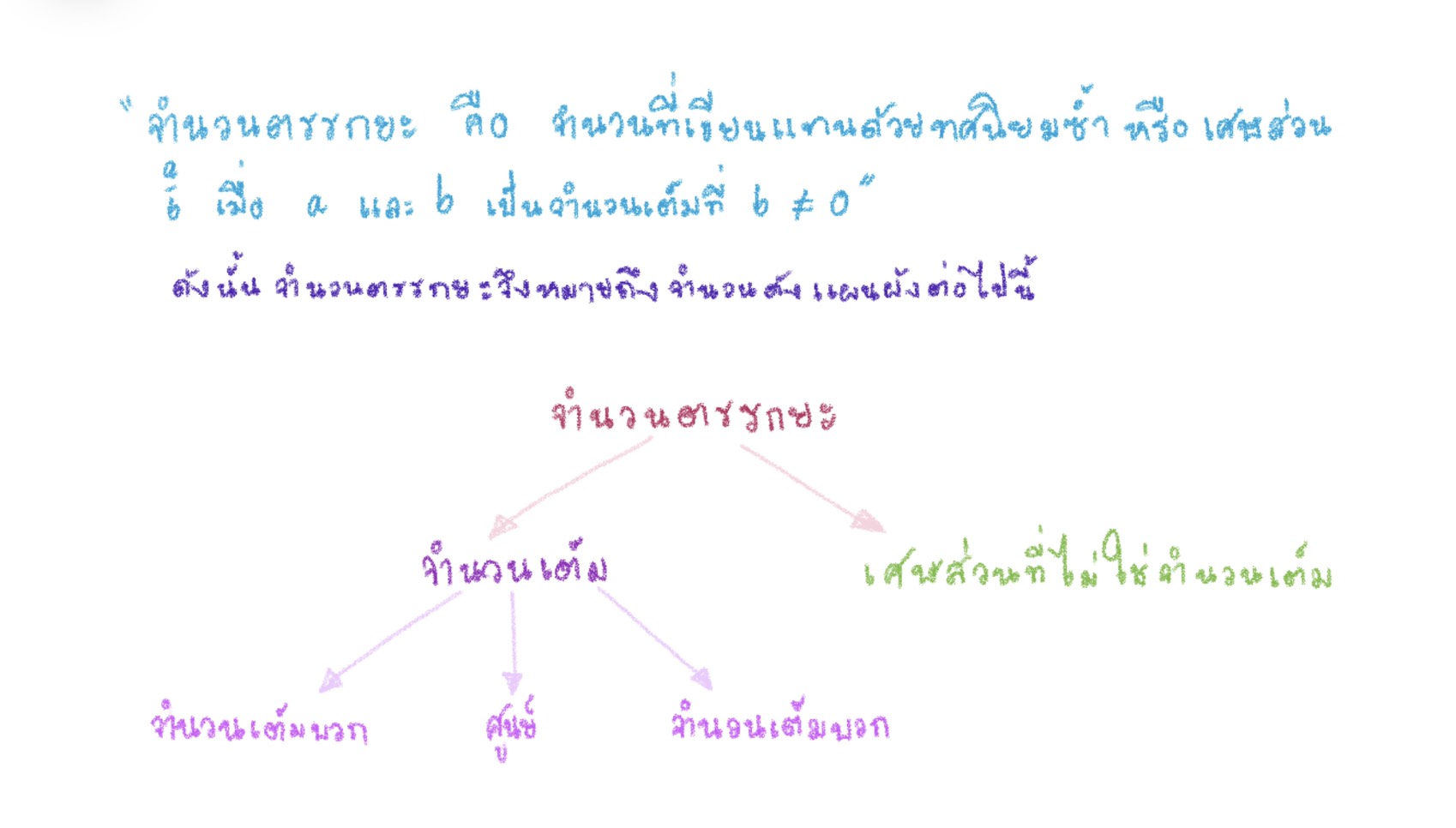
ความหมายของจำนวนตรรกยะ



ในทำนองเดียวกันกับเศษส่วนอื่นๆ ก็สามารถเปลี่ยนเป็นทศนิยมได้ ดังนี้
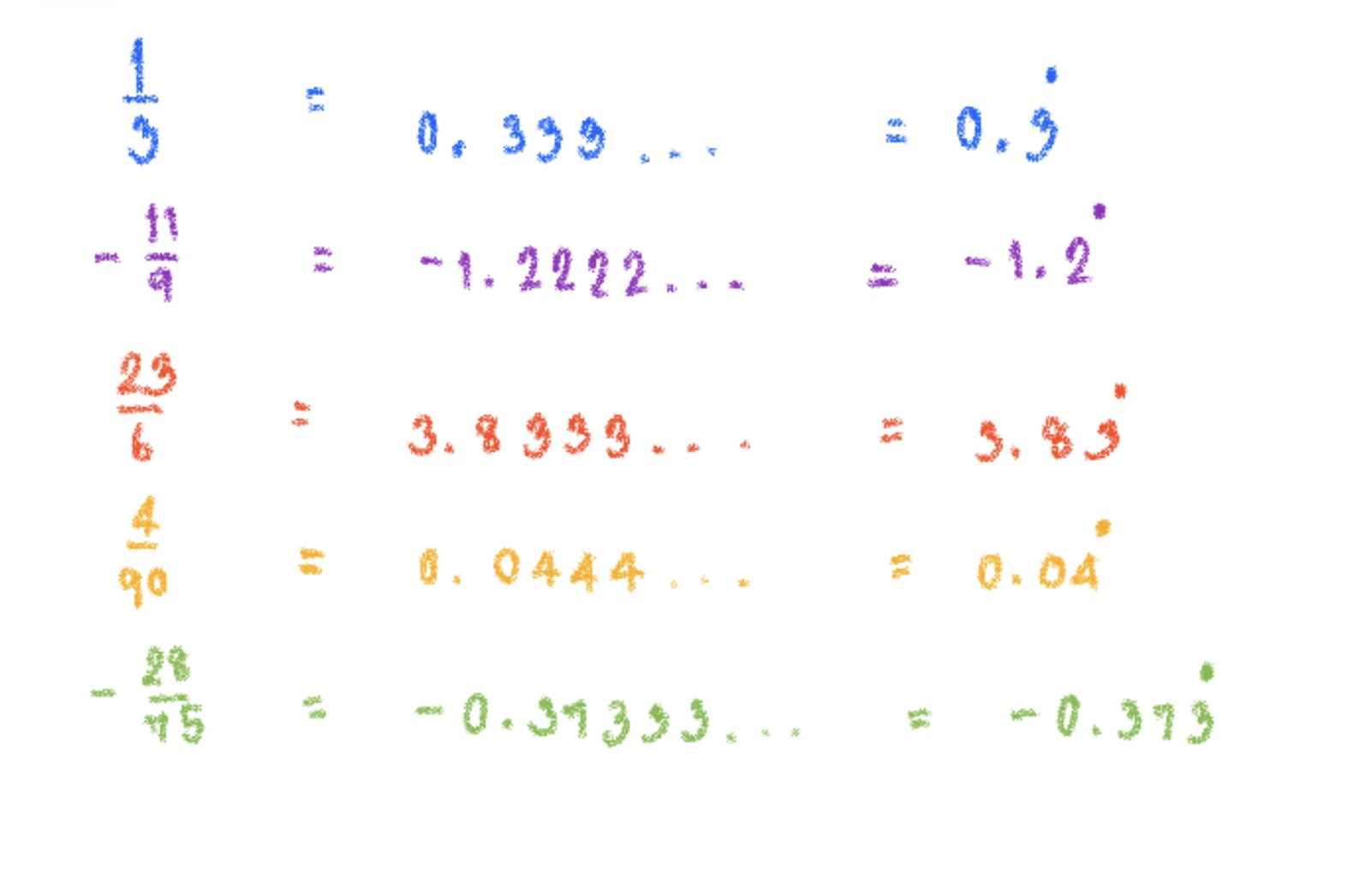
จะเห็นว่าเศษส่วนทุกจำนวนสามารถเปลี่ยนเป็นทศนิยมได้ และทศนิยมที่ได้ก็จะมี 2 ลักษณะด้วยกัน คือ ทศนิยมแบบซ้ำศูนย์ กับทศนิยมแบบไม่ซ้ำศูนย์
ทศนิยมแบบซ้ำศูนย์ เช่น 1.20. แต่เวลาเขียนจะเป็น 1.2 เท่านั้น บางครั้งจึงเรียกว่าเป็นทศนิยมแบบรู้จบ ซึ่งสามารถนับจำนวนทศนิมที่อยู่หลังจุดได้
ทศนิยมซ้ำที่ไม่ใช่ศูนย์ เช่น เป็นต้น ทศนิยมเหล่านี้จะเรียกว่าทศนิยมแบบรู้จบแบบซ้ำ เพราะไม่สามารถนับจำนวนตัวเลขที่อยู่หลังจุดได้ แต่สามารถบอกถึงทศนิยมตัวต่อไปได้ว่าเป็นตัวใด
เมื่อเราสามารถขียนเศษส่วนเป็นทศนิยมได้ ดังนั้นในทางกลับกันเราก็สามารเปลี่ยนทศนิยมซ้ำศูนย์หรือซ้ำอื่นๆ ให้เป็นเศษส่วนได้ดังตัวอย่างต่อไปนี้

จากที่กล่าวมาพบว่า เศษส่วนสามารถเขียนให้อยู่ในรูปทศนิยมซ้ำ หรือทศนิยมซ้ำสามารถเขียนให้อยู่ในรูปเศษส่วนได้ ดังนั้นจึงกล่าวได้ว่า