การให้เหตุผลแบบนิรันัย

การให้เหตุผลแบบนิรนัย คือ การมองจากสิ่งใหญ่ๆว่ามันเป็นจริง ทำให้สิ่งที่อยู่ในนั้น จริงตามไปด้วย

การสรุปผลของนิรนัยจะถูกต้องก็ต่อเมื่อเป็นการสรุปที่สมเหตุสมผล

เช่น เราไปซื้อผลไม้ แล้วแม่ค้าบอกว่า ผลไม้กองนี้หวาน แสดงว่า ถ้าหยิบมา 2 ลูก เราสามารถบอกได้เลยว่า ผลไม้ 2 ลูกนั้นหวาน

การให้เหตุผลแบบนิรนัยนั้น จะแตกต่างกับ การให้เหตุผลแบบอุปนัย

อุปนัย มองจากเล็ก ไปหา ใหญ่

นิรนัย มองจาก ใหญ่ ไปหา เล็ก

การตรวจสอบความสมเหตุสมผล ของการให้เหตุผลแบบนิรนัย

วิธีการตรวจสอบมีหลายวิธี แต่พี่จะแนะนำการตรวจสอบที่ทำให้น้องๆเข้าใจง่ายที่สุด ซึ่งก็คือตรวจสอบโดยใช้แผนภาพเวนน์-ออยเลอร์

ถ้าแผนภาพที่เราวาด เป็นไปตามผลสรุป(ตามที่โจทย์บอก)ทุกกรณี แสดงว่า ผลสรุปนั้นสมเหตุสมผล

แต่ถ้าแผนภาพที่เราวาดนั้นไม่เป็นตามที่สรุปไว้ คืออาจจะมีบางกรณีที่ไม่จริง ผลสรุปนั้นจะไม่สมเหตุสมผล

เรามาดูตัวอย่างกันดีกว่าค่ะ

ตัวอย่าง การให้เหตผลแบบนิรนัย

โจทย์เกี่ยวกับการให้เหตุผลแบบนิรนัย เป็นโจทย์ที่ถ้าเราเข้าใจมันจะสนุกมากๆ ลองไปดูตัวอย่างกันค่ะ

1.)

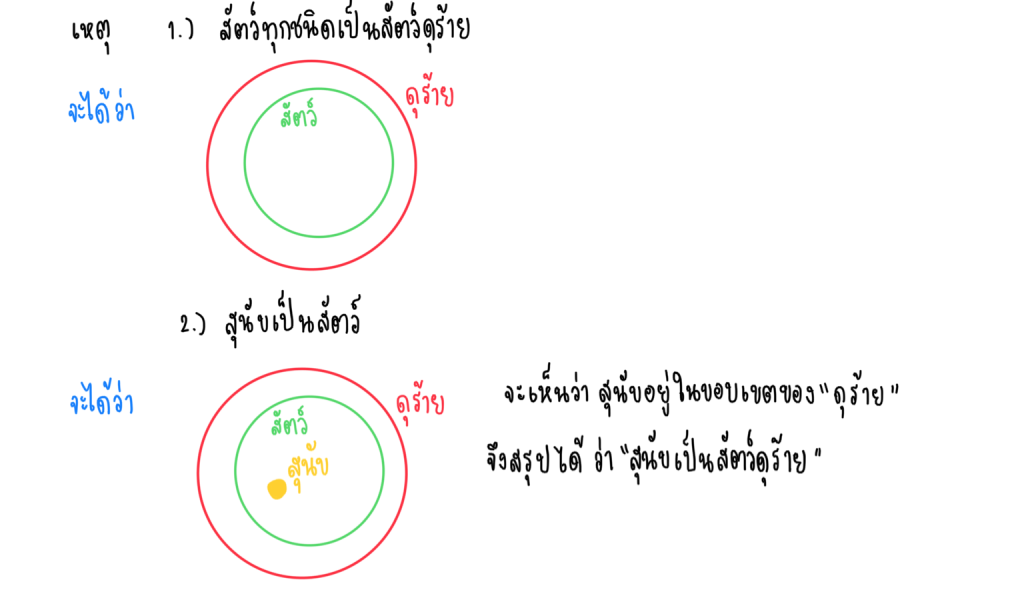
เหตุ 1.สัตว์ทุกตัวเป็นสัตว์ดุร้าย

2. สุนัขเป็นสัตว์

ผล        สุนัขเป็นสัตว์ดุร้าย

ตอบ การให้เหตุผลนี้ สมเหตุสมผล

คำอธิบาย การให้เหตุผลแบบนิรนัย คือเราจะยอมรับว่าเหตุที่ 1 เป็นจริง แล้ว เหตุที่ 2 เกิดจากเราสร้างขึ้นมา เหมือนกับข้อนี้ ที่บอกว่าสัตว์ทุกตัวเป็นสัตว์ดุร้าย เราเลยสร้างเหตที่ 2 ขึ้นมาว่า ถ้าสุนัขเป็นสัตว์ล่ะ เราเลยสรุปผลว่า สุนัขเป็นสัตว์ดุร้าย

มาดูภาพประกอบเพื่อให้เข้าใจง่ายขึ้นค่ะ

2.)

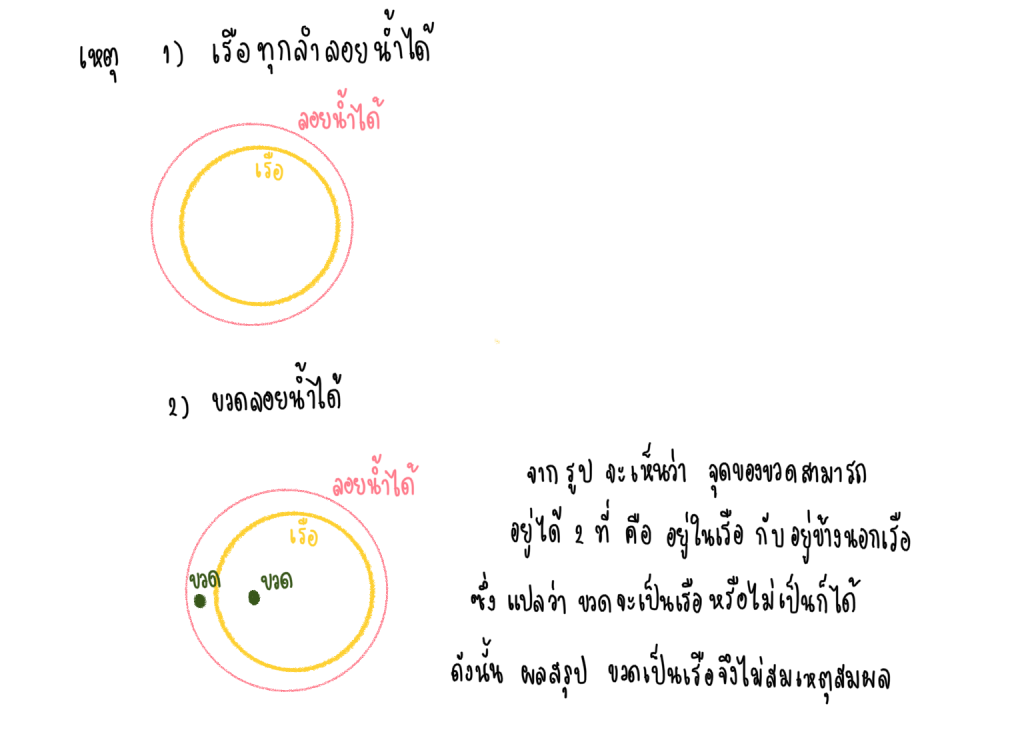
เหตุ 1. เรือทุกลำลอยน้ำได้

2. ขวดลอยน้ำได้

ผล            ขวดเป็นเรือ

ตอบ ไม่สมเหตสมผล

ข้อนี้เราจะใช้รูปภาพในการอธิบาย เพื่อไม่ให้น้องๆงงกันนะคะ

3.) เหตุ

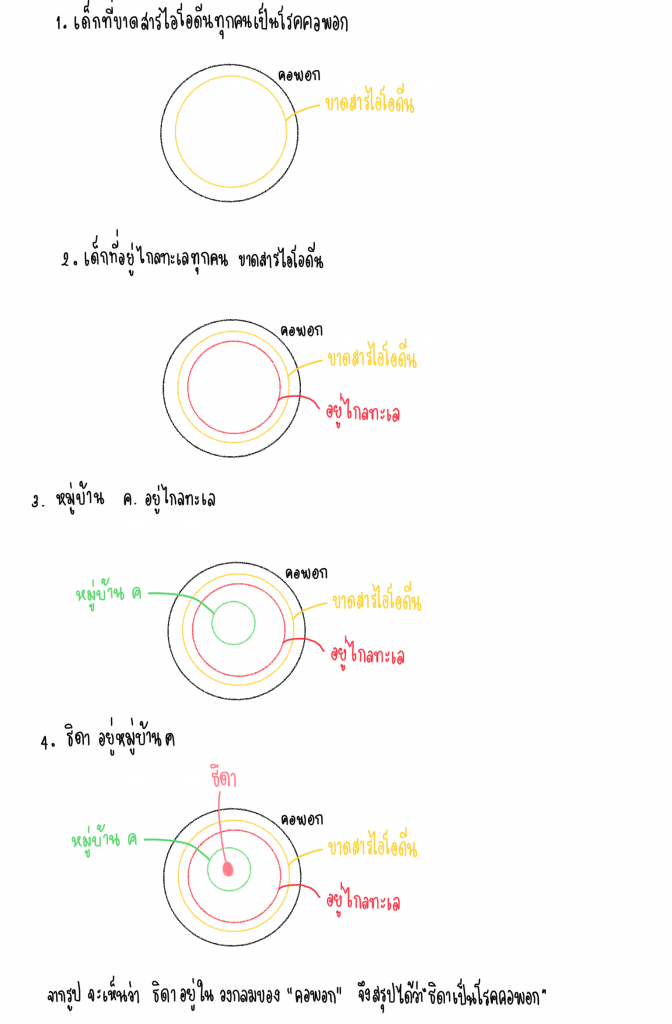
1. เด็กที่ขาดสารไอโอดีนทุกคนเป็นโรคคอพอก
2. เด็กที่อยู่ไกลทะเลทุกคน ขาดสารไอโอดีน
3. หมู่บ้าน ค อยู่ไกลจากทะเล
4. ธิดา อยู่หมู่บ้าน ก

ผล.       ธิดาเป็นโรคคอพอก

ตอบ ข้อความข้างต้นสมเหตุสมผล

อธิบายตัวอย่างข้างต้น

4.) เหตุ

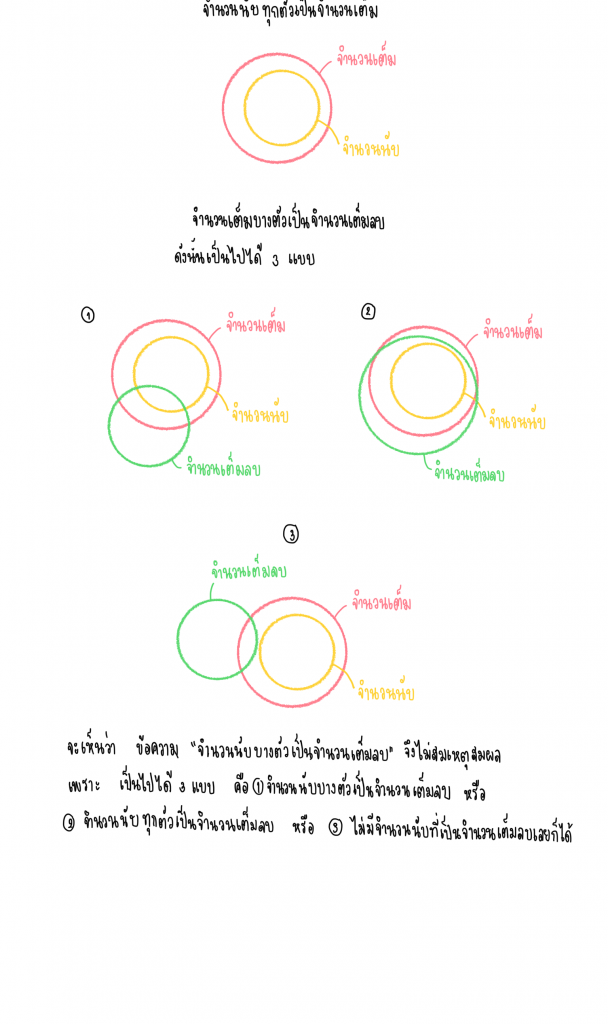
1. จำนวนนับทุกจำนวนเป็นจำนวนเต็ม
2. จำนวนเต็มบางจำนวนเป็นจำนวนเต็มลบ

ผล        จำนวนนับบางตัวเป็นจำนวนเต็มลบ

พิจารณา จากภาพ ดังนี้

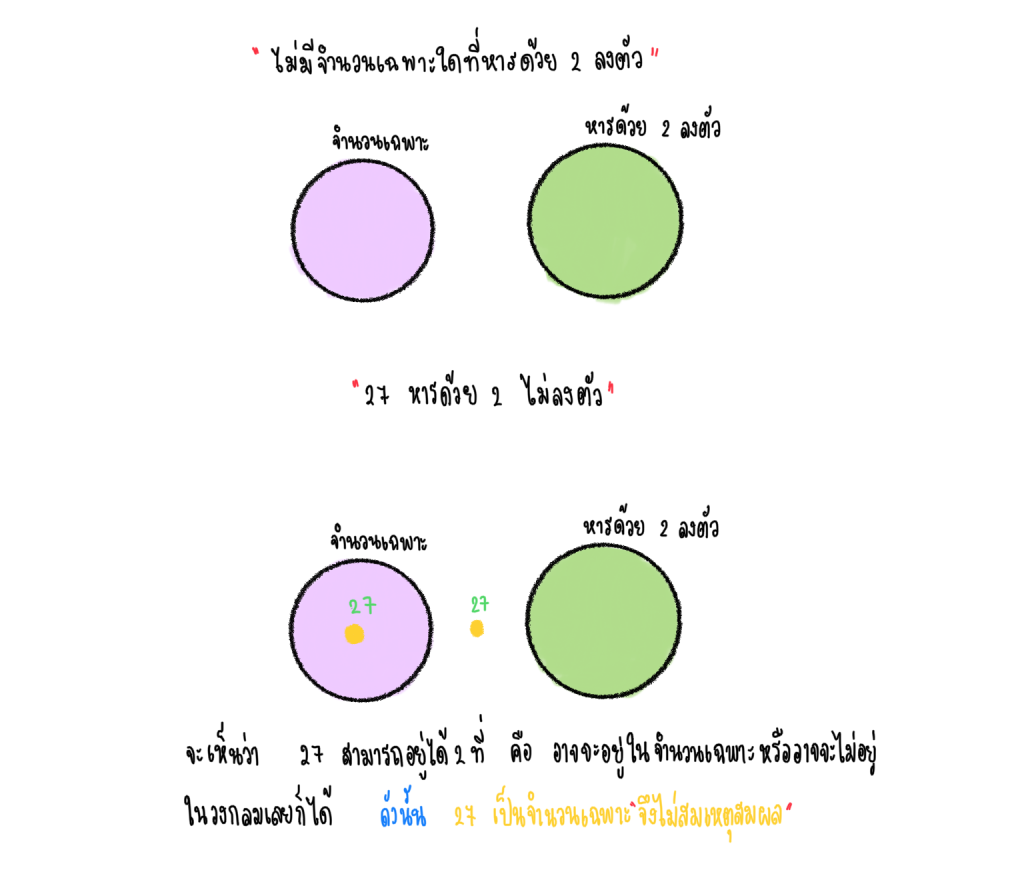
4.) เหตุ

1. ไม่มีจำนวนเฉพาะใดที่หารด้วย 2 ลงตัว
2. 27 หารด้วย 2 ไม่ลงตัว

ผล.      27 เป็นจำนวนเฉพาะ

ตอบ ไม่สมเหตุสมผล

อธิบายด้วยภาพ ดังนี้

การให้เหตุผลแบบอุปนัย กับ การให้เหตุผลแบบนิรนัย

อุปนัย

ใช้ประสบการณ์ หรือทำซ้ำๆ แล้วคาดคะเนผลสรุป

ไม่มีขอบเขตที่ชัดเจน

ผลสรุปอาจจะจริงหรือเท็จก็ได้

ยิ่งประสบการณ์มาก ผลสรุปยิ่งหน้าเชื่อถือ

น้องๆสามารถเข้าไปดูเนื้อหา การให้เหตุผลแบบอุปนัย ได้เลยนะคะ

นิรนัย

ยอมรับว่า เหตุที่ 1 เป็นจริง และสร้างเหตุการณ์ที่ 2 ขึ้นมา แล้วมาสรุปผล

ผลสรุปจะถูกต้องก็ต่อเมื่อ มันสมเหตุสมผล

ตรวจการสมเหตุสมผลได้ด้วย แผนภาพ เวนน์-ออยเลอร์ (ตรวจสอบง่ายสุด)

วีดีโอเพิ่มเติมเกี่ยวกับ การให้เหตุผลแบบนิรัย