ในหลายๆกิจกรรมของชีวิตประจำวันเรามักจะ พบเจอสิ่งก่อสร้างที่เป็นรูปเรขาคณิตสามมิติ ที่จำเป็นต้องใช้มีการคำนวณพื้นที่ผิวพื้นที่ผิวของปริซึมและทรงกระบอกมาใช้ในการทาสี ปูเบื้องเป็นต้น

พื้นที่ผิวของปริซึมและทรงกระบอก

สิ่งรอบตัวในชีวิตประจำวันของเราหลายสิ่งที่ส่วนประกอบมีลักษณะเป็นรูปเรขาคณิตสามมิติ เช่น กล่องใส่กระดาษและตู้มีลักษณะเป็นทรงสี่เหลี่ยมมุมฉาก ปิ่นโตและกระป๋องนมข้นหวานมีลักษณะเป็นทรงกระบอก ไอศกรีมบรรจุอยู่ในกรวยที่ทำจากแป้งอบกรอบลูกโลกและลูกบอลมีลักษณะใกล้เคียงกับทรงกลม

การหาพื้นที่ผิวของรูปเรขาคณิตสามมิติใดๆ เป็นการหาพื้นที่ของพื้นที่ผิวทั้งหมดของรูปเรขาคณิตสามมิตินั้นๆ

ปริซึม

สิ่งของที่อยู่รอบตัวเรา หลายอย่างมีลักษณะเป็นปริซึม เช่น กล้องสลับลายมีลักษณะเป็นปริซึมสามเหลี่ยม กล่องยาสีฟันมีลักษณะเป็นปริซึมสี่เหลี่ยมเป็นต้น

ทรงกระบอก

ทรงกระบอกเป็นรูปเรขาคณิตสามมิติที่มีรูปร่างคล้ายกระบอกไม้ไผ่ที่คัดเป็นท่อน มีหลายสิ่งที่มีคำว่ากระบอกอยู่ในชื่อเพื่อบ่งบอกให้รู้ว่ามีส่วนเกี่ยวข้องกับทรงกระบอก เช่น เสื้อแขนกระบอก หุ่นกระบอก หรือปลากระบอบ นอกจากนี้รอบ ๆ ตัวเรายังมีสิ่งของอีกหลายสิ่งที่ส่วนประกอบมีลักษณะเป็นทรงกระบอก เช่น แก้วน้ำ แจกัน และถ่านไฟฉาย

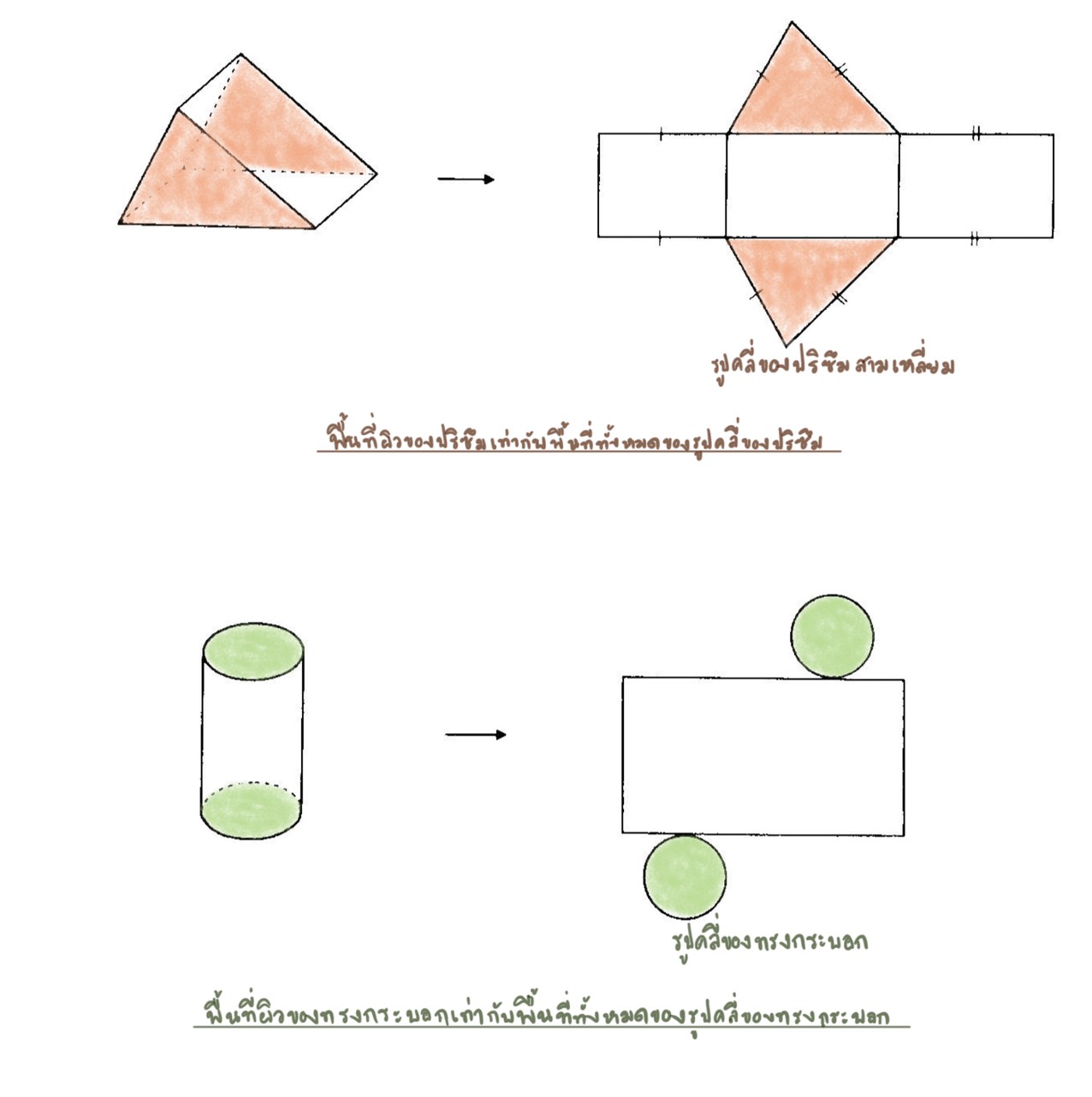
การหาพื้นที่ผิวของปริซึมและทรงกระบอก หาได้โดยการหาพื้นที่ของด้านข้างทั้งหมด รวมกับพื้นที่ของฐานทั้งสอง ซึ่งอธิบายโดยใช้รูปคลี่ได้ ดังนี้

ตัวอย่าง1 ห้องทรงสี่เหลี่ยมมุมฉากห้องหนึ่ง กว้าง 3 เมตร ยาว 4.5 เมตร และสูง 3เมตร ต้องการทาสีเพดาน และผนังห้องภายในทั้งสี่ด้าน บริเวณที่ทาสีจะมีพื้นที่เท่าใด

ตัวอย่าง2 ช็อกโกแลตก้อนหนึ่งมีลักษณะเป็นปริซึมสามเหลี่ยมหน้าจั่วดังรูป จะต้องใช้กระดาษห่อช็อกโกแลตที่มีพื้นที่อย่างน้อยเท่าใด

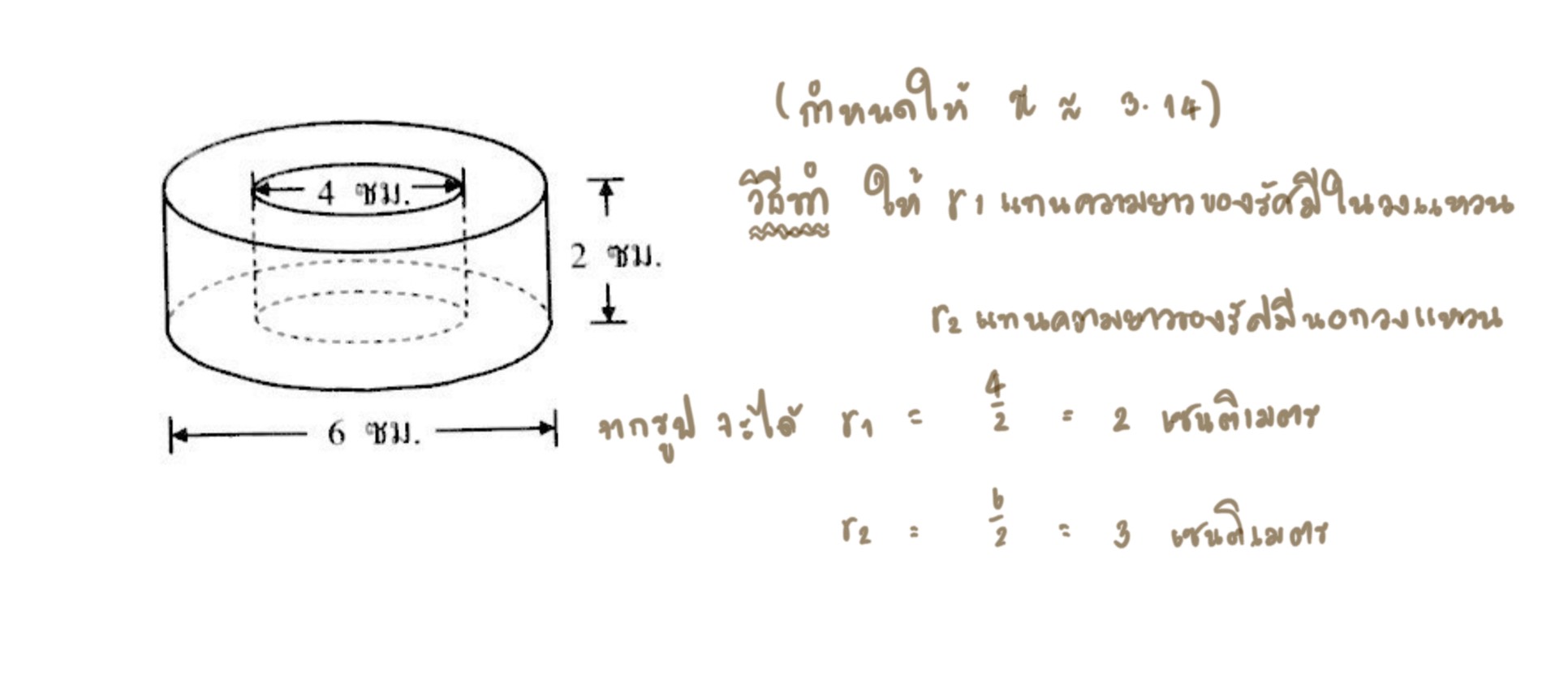
ตัวอย่าง3 วงแหวนโลหะมีลักษณะและขนาดดังรูป ถ้านำวงแหวนนี้ไปชุปสี พื้นที่ผิวของวงแหวนที่เคลือบสีจะเป็นเท่าใด

คลิปวิดีโอตัวอย่างเรื่องพื้นที่ผิวของปริซึมและทรงกระบอก