ประมาณค่าทศนิยมด้วยการปัดทิ้งและปัดทด

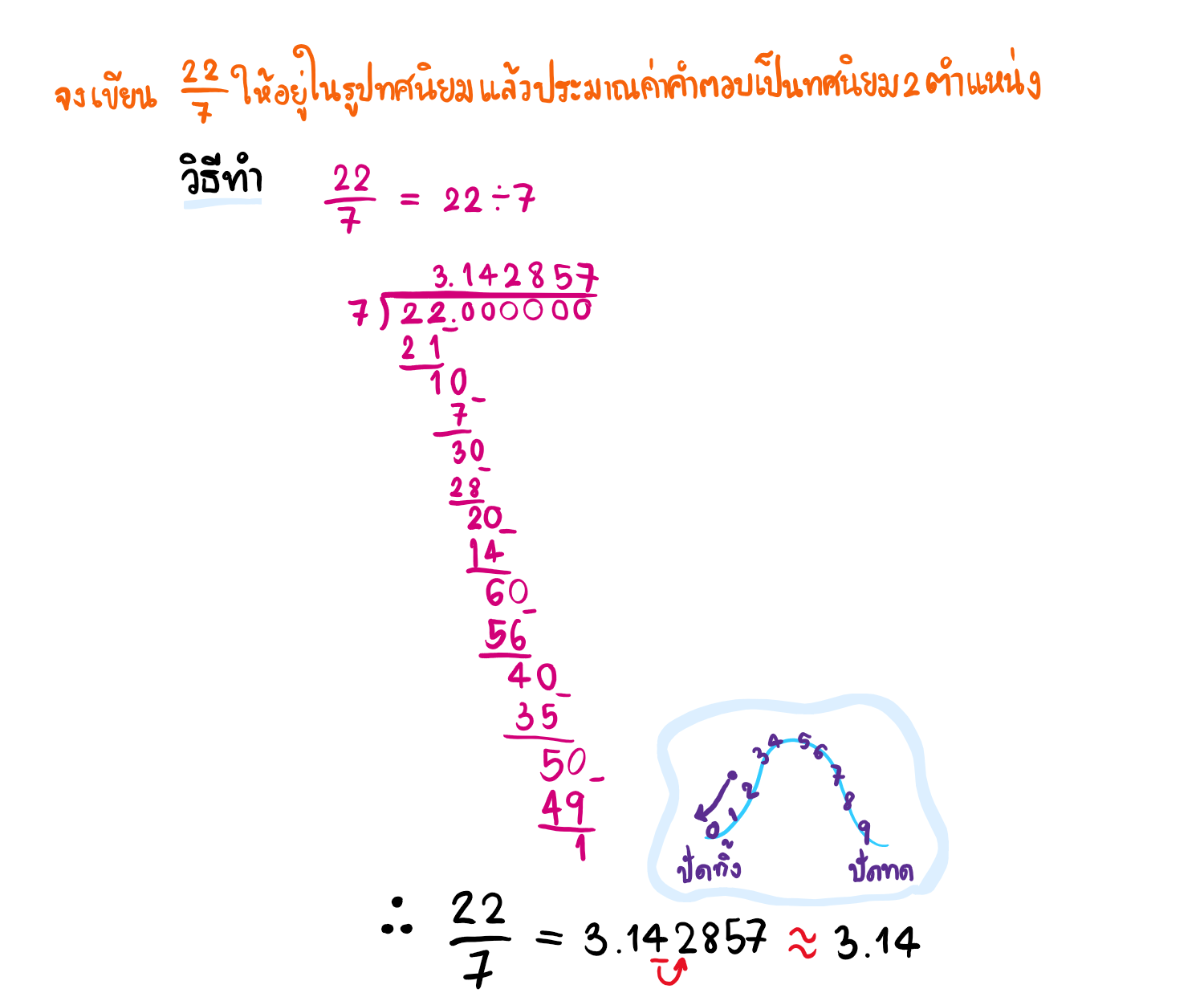
บทความนี้จะพูดถึงเรื่องพื้นฐานของทศนิยมอีก 1 เรื่องก็คือการประมาณค่าใกล้เคียงของทศนิยม น้อง ๆคงอาจจะเคยเรียนการประมาณค่าใกล้เคียงของจำนวนเต็มมาแล้ว การประมาณค่าทศนิยมหลักการคล้ายกับการประมาณค่าจำนวนเต็มแต่อาจจะแตกต่างกันที่คำพูดที่ใช้ เช่นจำนวนเต็มจะใช้คำว่าหลักส่วนทศนิยมจะใช้คำว่าตำแหน่ง บทความนี้จึงจะมาแนะนำหลักการประมาณค่าทศนิยมให้น้อง ๆเข้าใจ และสามารถประมาณค่าทศนิยมได้อย่างถูกต้อง

tucksaga

การประมาณค่าทศนิยมป.5, คณิตศาสตร์, คณิตศาสตร์ ป.5, ทศนิยมป.5, ป.5, ประมาณค่าทศนิยม

Add LINE friends for one click to find article.

หลักการประมาณค่าทศนิยมมีขั้นตอนดังนี้

1.พิจารณาเลขโดดที่อยู่ข้างหลังตำแหน่งที่โจทย์ต้องการประมาณค่า เช่น 3.142857 ประมาณค่าใกล้เคียงทศนิยมให้อยู่ในรูปทศนิยม 2 ตำแหน่ง ตำแหน่งที่ 2 คือหมายเลข 4 ดังนั้นต้องพิจารณาเลขโดดที่อยู่ข้างหลังหมายเลข 4 นั่นคือเลข 2

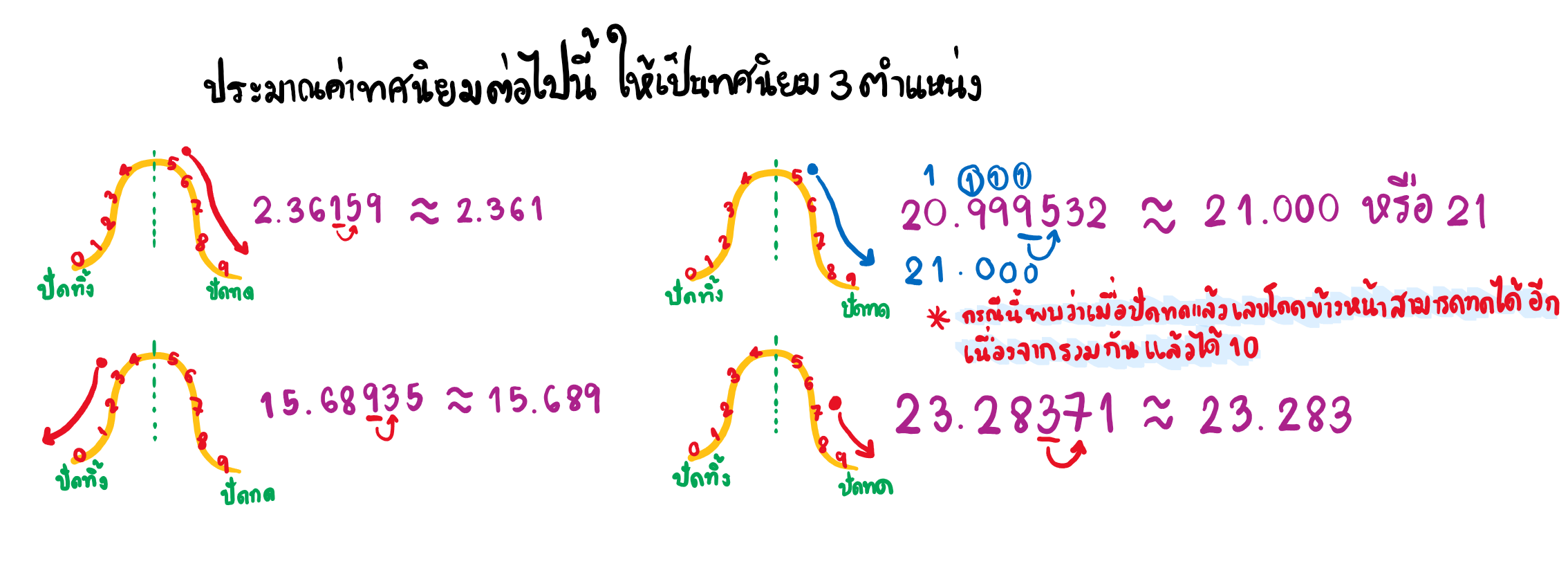
2.พิจารณาว่าเลขโดด อยู่ในกลุ่มใด ถ้าเลขโดดเป็น 0-4 แสดงว่าอยู่ในกลุ่มที่ต้องปัดเศษทิ้ง ถ้าเลขโดดเป็น 5-9 แสดงว่าอยู่ในกลุ่มที่ต้องปัดเศษขึ้น หรือทด 1 ในตำแหน่งข้างหน้า

3.เมื่อพิจารณาว่าเลขโดดอยู่ในกลุ่มใดแล้วก็จะสามารถประมาณค่าทศนิยมออกมาได้ตามตำแหน่งที่เราต้องการ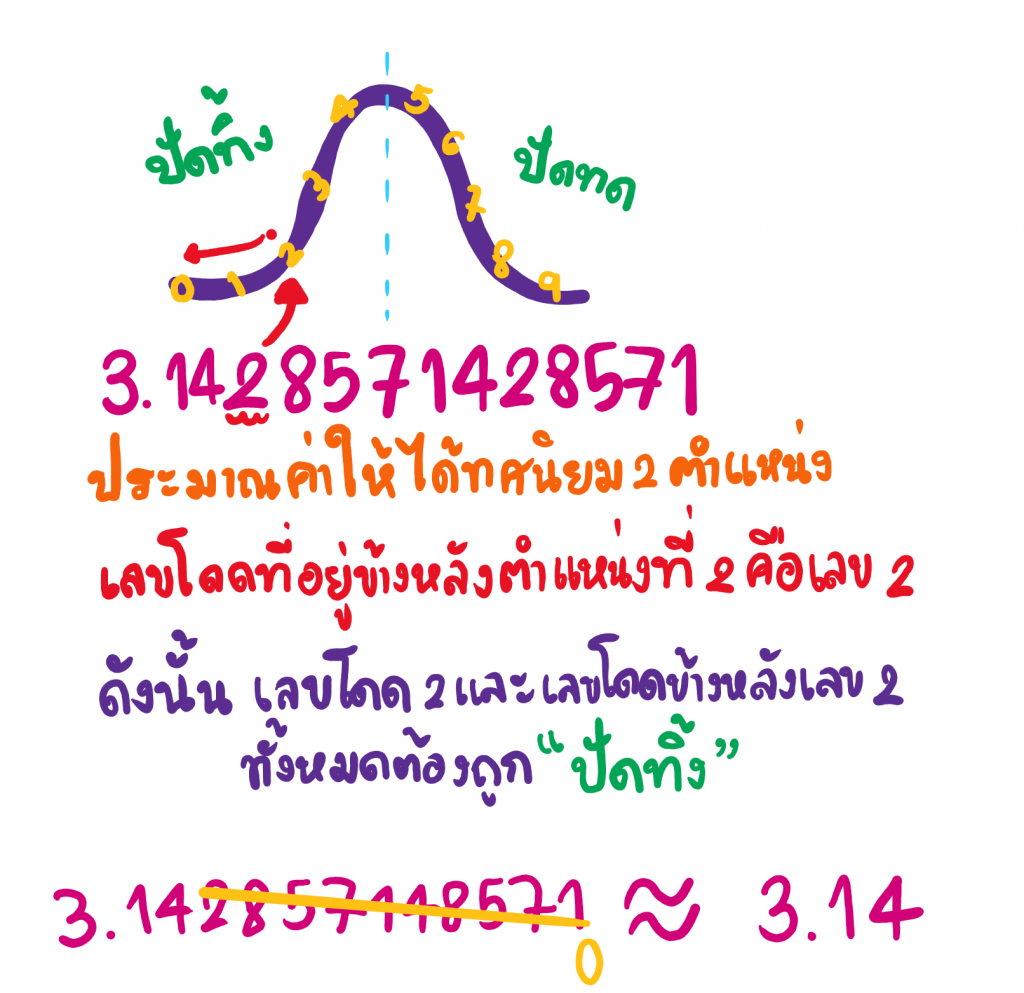

ประโยชน์ของการประมาณค่าทศนิยม

การประมาณค่าทศนิยมก็คือการปัดทศนิยมให้อยู่ในตำแหน่งที่ต้องการ มักจะใช้ในการหารทศนิยมเนื่องจากการหารทศนิยมนั้นมักจะได้คำตอบที่เป็นทศนิยมซ้ำหรือเป็นทศนิยมแบบไม่รู้จบการประมาณค่าทศนิยมจึงจะช่วยทำให้คำตอบมีตำแหน่งของทศนิยมที่สั้นลง

คลิปตัวอย่างเรื่องประมาณค่าทศนิยม

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

M2 V. to be + ร่วมกับ Who WhatWhere + -Like + infinitive

การใช้ V. to be ร่วมกับ Who/ What/Where และ Like +V. infinitive

สวัสดีค่ะนักเรียนชั้นม.2 ทุกคน วันนี้เราจะไปเรียนรู้เรื่อง การใช้ V. to be + ร่วมกับ Who/ What/Where + -Like + infinitive ซึ่งเป็นโครงสร้างที่สับสนบ่อย แต่ที่จริงแล้วง่ายมากๆ ไปลุยกันเลยจ้า Let’s go ความหมาย Verb to be

การบวก ลบ และคูณเมทริกซ์

การบวก ลบ และคูณเมทริกซ์ การบวก ลบ และคูณเมทริกซ์ เราจะนำสมาชิกของเมทริกซ์แต่ละเมทริกซ์มาบวก ลบ คูณกัน ซึ่งการดำเนินการเหล่านี้มีสมบัติและข้อยกเว้นต่างกันไป เช่น การบวกต้องเอาสมาชิกตำแหน่งเดียวกันมาบวกกัน เป็นต้น ต่อไปเราจะมาดูวิธีการบวก ลบ และคูณเมทริกซ์กันค่ะ การบวกเมทริกซ์ เมทริกซ์ที่จะนำมาบวกกันได้นั้น ต้องมีมิติเท่ากัน และการบวกจะนำสมาชิกตำแหน่งเดียวกันมาบวกกัน เช่น 1.) 2.) การลบเมทริกซ์ การลบเมทริกซ์จะคล้ายๆกับการบวกเมทริกซ์เลย

Present Continuous Tense

สวัสดีนักเรียนชั้นม.3 ที่น่ารักทุกคนค่า วันนี้เราจะไปเรียนรู้กันเรื่อง ” Present Continuous Tense” พร้อมทั้งตัวอย่างสถานการณ์ใกล้ตัว และข้อสอบวัดความเข้าใจหลังเรียนแบบปังๆกันจร้า หากพร้อมแล้วก็ไปลุยกันเลย เริ่มกับการใช้ Present Continuous Tense อธิบายสิ่งที่กำลังเกิดขึ้นอยู่ในขณะนั้น เช่น Danniel is playing a football at the moment.

การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์

การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ การตรวจสอบคู่อันดับที่เป็นความสัมพันธ์ คือการตรวจสอบคู่อันดับว่าคู่ไหนเป็นความสัมพันธ์ที่ตรงกับเงื่อนไขที่กำหนด จากที่เรารู้กันในบทความเรื่อง ความสัมพันธ์ว่า r จะเป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ A × B แต่ถ้าเราใส่เงื่อนไขบางอย่างเข้าไป ความสัมพันธ์ r ที่ได้ก็อาจจะจะเปลี่ยนไปด้วย แต่ยังคงเป็นสับเซตของ A × B เหมือนเดิม

รากที่ n ของจำนวนจริง และจำนวนจริงในรูปกรณฑ์

รากที่ n ของจำนวนจริง รากที่ n ของจำนวนจริง คือจำนวนจริงตัวหนึ่งยกกำลัง n แล้วเท่ากับ x เมื่อ n > 1 เราสามารถตรวจสอบรากที่ n ได้ง่ายๆ โดยนิยามดังนี้ นิยาม ให้ x, y เป็นจำนวนจริง และ n

เรียนรู้บทร้องกรองสุภาษิต ตนเป็นที่พึ่งแห่งตน

การนำสุภาษิตมาแต่งเป็นบทร้อยกรอง เรียกว่า บทประพันธ์ร้อยกรองสุภาษิต ซึ่งบทที่น้อง ๆ จะได้เรียนกันในวันนี้คือบทร้อยกรองสุภาษิตเรื่อง ตนเป็นที่พึ่งแห่งตน เราไปดูกันเลยค่ะว่าที่มจากของบทร้อยกรองนี้จะเป็นอย่างไร มาจากสุภาษิตอะไร รวมไปถึงถอดความหมายตัวบท ศึกษาคำศัพท์ที่น่ารู้และศึกษาคุณค่าที่อยู่ในเรื่องด้วยค่ะ ถ้าพร้อมแล้วเราไปดูพร้อมกันเลย ความเป็นมา ตนเป็นที่พึ่งแห่งตน ตนเป็นที่พึ่งแห่งตน ผู้แต่งคือ นายเพิ่ม สวัสดิ์วรรณกิจ เป็นบทร้อยกรองประเภทกลอนแปด พิมพ์รวมอยู่ในหนังสือบทประพันธ์อธิบายสุภาษิตของวรรณคดีสมาคมแห่งประเทศไทย

ประมาณค่าทศนิยมด้วยการปัดทิ้งและปัดทด

สารบัญ