จุด : เรขาคณิตวิเคราะห์

supanaree

คณิตศาสตร์, คณิตศาสตร์ เพิ่มเติม, ม.4, เรขาคณิตวิเคราะห์

Add LINE friends for one click to find article.

จุด

จุด เป็นตัวบอกตำแหน่งของสิ่งต่างๆ เช่น ตำแหน่งของสถานที่ต่างๆ ในเรื่องเรขาคณิตวิเคราะห์ จุดใช้บอกตำแหน่งในระนาบ 2 มิติ หรือ 3 มิติ เช่น

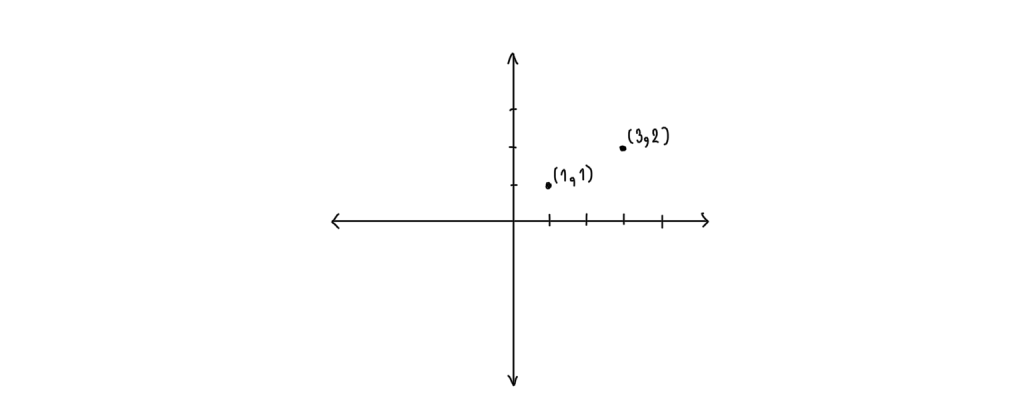
ระยะทางระหว่างจุดสองจุด

เราสามารถหาระยะทางระหว่างจุดสองจุดได้ โดยใช้สูตร

โดยจะกำหนดให้ $\inline P_{1}(x_{1},y_{1})$ และ $\inline P_{2}(x_{2},y_{2})$ เป็นจุดในระนาบ เราจะได้ว่าระยะห่างระหว่างจุดทั้งสองหาได้จาก

$\inline \mathbf{{\color{DarkOrange} \left | P_{1}P_{2} \right | = \sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}}$

ตัวอย่าง

ระยะห่างระหว่าง A(1,1) และ B(3,2) คือ $จุด$

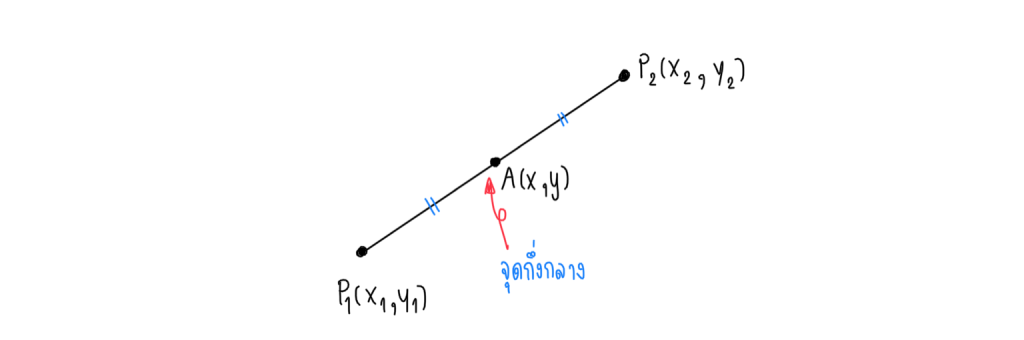
จุดกึ่งกลางของส่วนของเส้นตรง

ให้ A(x, y) เป็นจุดกึ่งกลางของเส้นตรงที่มีจุดปลายคือจุด $\inline P_1(x_1,y_1)$ และ $\inline P_2(x_2,y_2)$ จะได้ว่า $\inline x=\frac{x_1+x_2}{2}$ และ $\inline y=\frac{y_1+y_2}{2}$

ตำแหน่งของจุดกึ่งกลางเป็นดังรูป

ตัวอย่าง

จุดแบ่งส่วนของเส้นตรงที่ไม่ใช่จุดกึ่งกลาง

กรณีที่จุด A(x, y) เป็นจุดแบ่งเส้นตรงที่ไม่ใช่จุดกึ่งกลาง เช่น

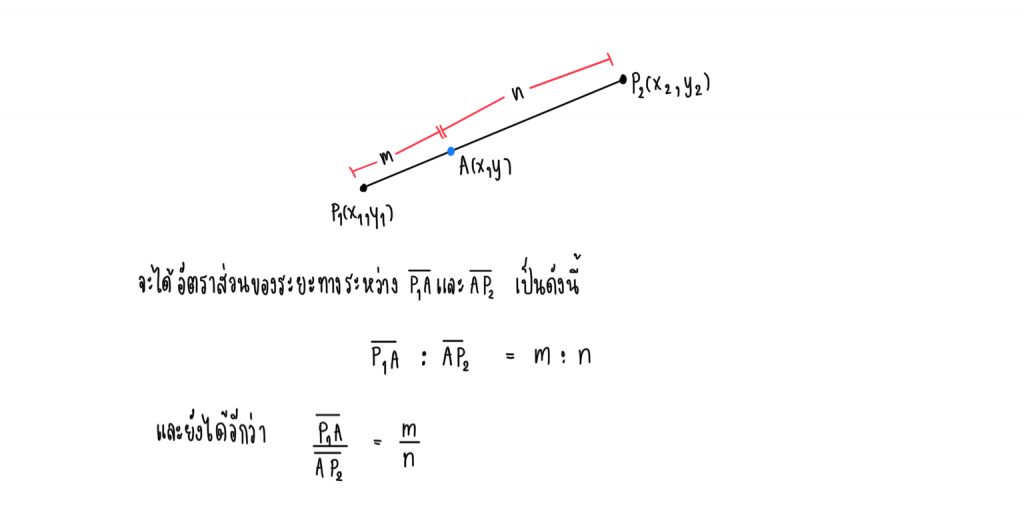
จะได้ว่า ${\color{DarkOrange} x=\frac{nx_1+mx_2}{m+n}}$ และ ${\color{DarkOrange} y=\frac{ny_1+my_2}{m+n}}$

จุดตัดของเส้นมัธยฐาน

เส้นมัธยฐานคือเส้นตรงที่ลากจากจุดกึ่งกลางของเส้นตรงไปยังจุดยอดด้านตรงข้าม ดังรูป

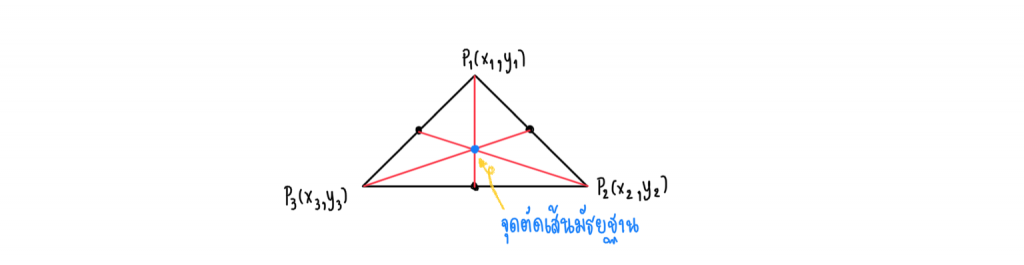
จากที่น้องๆทราบกันแล้วว่าจุดตัดเส้นมัธยฐานอยู่ตรงไหน ต่อไปเราจะหาพิกัดของจุดตัดนั้นนั้น ซึ่งหาได้จาก

${\color{DarkOrange} x=\frac{x_1+x_2+x_3}{3}}$ และ ${\color{DarkOrange} y=\frac{y_1+y_2+y_3}{3}}$

ตัวอย่างเกี่ยวกับ จุด

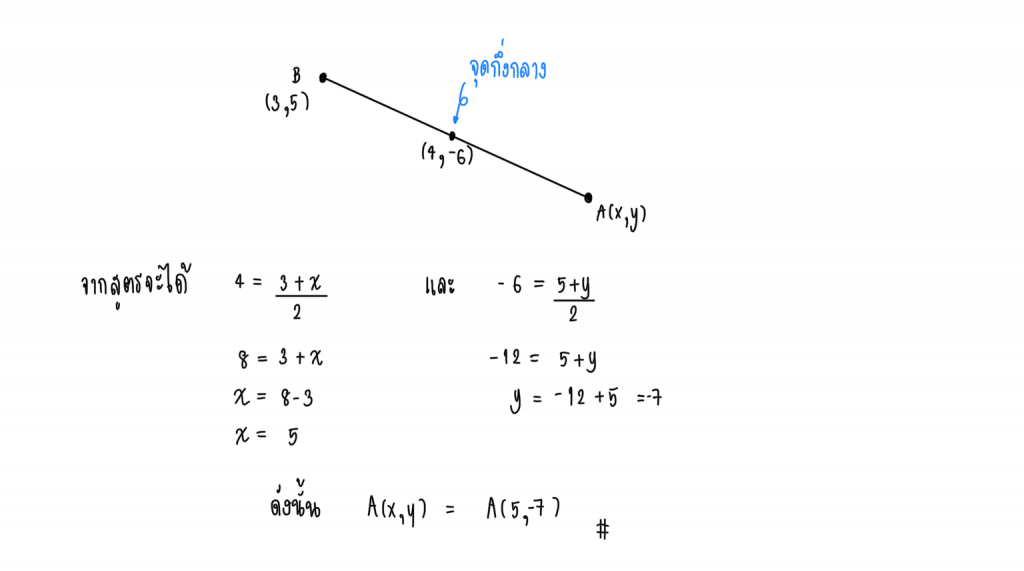
1.) ถ้า A(x, y) และ B(3, 5) มีจุดกึ่งกลางคือ (4, -6) จงหาพิกัด A(x, y)

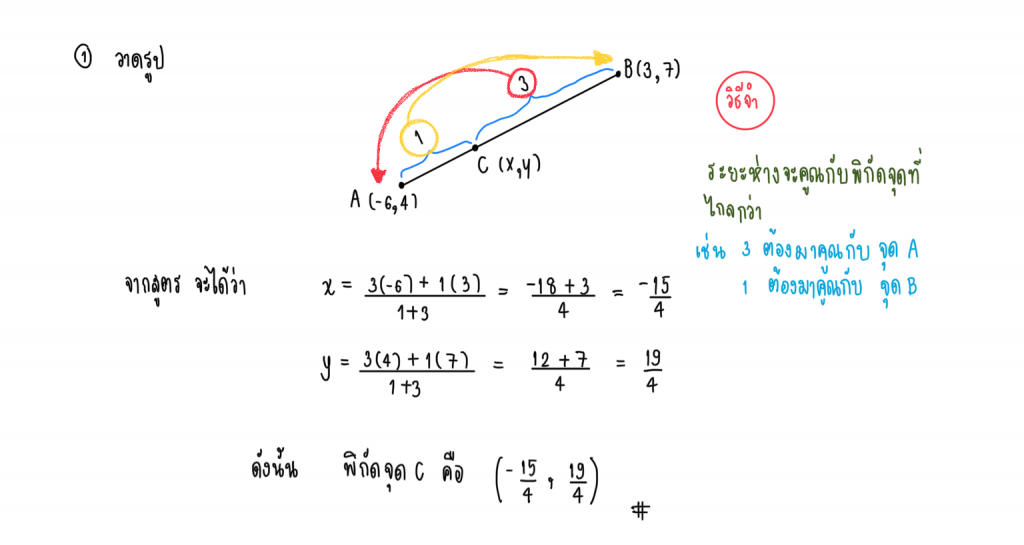
2.) ให้ A(-6, 4) B(3, 7) เป็นจุดปลายของส่วนของเส้นตรง จงหาพิกัดของ C บนส่วนของเส้นตรง $\overline{AB}$ โดยที่ $\overline{AC}:\overline{CB}=1:3$

3.) หาความยาวของเส้นมัธยฐานของรูปสามเหลี่ยม ABC เมื่อกำหนดให้ พิกัด A, B และ C มีพิกัดเป็น (3, 2), (1, -3) และ (5, -3) ตามลำดับ

NockAcademy คือโรงเรียนออนไลน์สำหรับเด็ก โดยแอปฯ และเว็บไซต์ นักเรียนสามารถเรียนรู้ผ่านคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย
มากไปกว่านั้น เรายังมีคอร์สเรียนออนไลน์ การสอนพิเศษ การติวนอกสถานที่โดยติวเตอร์ที่แน่นไปด้วยความรู้ อีกด้วย

แค่ 10 นาที ก็เข้าใจได้

สามารถดูคลิปบทเรียนวิชา คณิตศาสตร์ ภาษาอังกฤษ และภาษาไทย ที่มีมากกว่า 2,000+ คลิป และยังสามารถทำแบบทดสอบที่มีมากกว่า 4000+ ข้อ

แนะนำ

แชร์

Second Conditional Sentence: ประโยคเงื่อนไขแบบที่ 2

สวัสดีน้องๆ ม. 5 ทุกคนนะครับ วันนี้เราจะมาเรียนรู้เกี่ยวกับ Conditional Sentence หรือ If Clause รูปแบบที่ 2 กันครับ ถ้าพร้อมแล้วไปดูกันเลย

เรียนรู้และทำความเข้าใจการใช้คำในภาษาไทยอย่างง่ายๆ

การใช้คำในภาษาไทย มีความสำคัญมาก แม้ว่าน้อง ๆ จะคุ้นเคยกับภาษาไทยดีในระดับหนึ่งแล้ว แต่แน่ใจหรือเปล่าคะว่าใช้คำกันได้อย่างถูกต้องแล้ว เพราะการใช้คำให้ถูกก็ถือเป็นเรื่องสำคัญค่ะ ดังนั้นบทเรียนหลักภาษาไทยในวันนี้จะพาน้อง ๆ ไปเรียนรู้เรื่องการใช้คำต่าง ๆ ได้ถูกต้องกันค่ะ จะมีอะไรบ้างไปเรียนรู้พร้อม ๆ กันเลยค่ะ การใช้คำ การใช้คำกำกวม คำกำกวม คือ การใช้คำหรือภาษาที่มีความหมายไม่ชัดเจน เป็นเหตุให้การสื่อสารผิดพลาด

การวัดความยาวส่วนโค้ง

การวัดความยาวส่วนโค้ง การวัดความยาวส่วนโค้ง ในบทความนี้จะเป็นการวัดความยาวของวงกลม 1 หน่วย วงกลมหนึ่งหน่วย คือวงกลมที่มีจุดศูนย์กลางที่จุดกำเนิด และมีรัศมียาว 1 หน่วย จากสูตรของเส้นรอบวง คือ 2r ดังนั้นวงกลมหนึ่งหน่วย จะมีเส้นรอบวงยาว 2 และครึ่งวงกลมยาว จุดปลายส่วนโค้ง จากรูป จะได้ว่าจุด P เป็นจุดปลายส่วนโค้ง จากที่เราได้ทำความรู้จักกับวงกลมหนึ่งหน่วยและจุดปลายส่วนโค้งแล้ว

Present Continuous Tense

สวัสดีนักเรียนชั้นม.2 ที่น่ารักทุกคน วันนี้เราจะไปเรียนรู้เรื่อง” Present Continuous Tense” พร้อมทั้งตัวอย่างสถานการณ์ใกล้ตัว และเทคนิคการจำและนำ Tense ไปใช้กันจร้า หากพร้อมแล้วก็ไปลุยกันเลย การใช้ Present Continuous Tense อธิบายสิ่งที่กำลังเกิดขึ้นอยู่ในขณะนั้น เช่น Danniel is playing a football at

ศัพท์บัญญัติ เรียนรู้การยืมคำและบัญญัติขึ้นใหม่

น้อง ๆ หลายคนอาจจะไม่ค่อยคุ้นเคยกับคำว่า ศัพท์บัญญัติ สักเท่าไหร่ บทเรียนวันนี้จะพาน้อง ๆ ไปทำความรู้จักกับศัพท์บัญญัติที่ว่านั่นกันค่ะว่าคืออะไร มีที่มาและมีหลักเกณฑ์ในการสร้างอย่างไรบ้าง ถ้าน้อง ๆ พร้อมที่จะเรียนรู้กันแล้ว ก็ไปศึกษาเรื่องนี้พร้อมกันเลยค่ะ การบัญญัติศัพท์คืออะไร การบัญญัติศัพท์ คือการกำหนดคำศัพท์จากภาษาต่างประเทศขึ้นมาใหม่ในภาษาไทย เพื่อใช้สื่อความหมายบางอย่างโดยเฉพาะในศาสตร์แขนงใดแขนงหนึ่ง หรือเพื่อใช้ในการเขียนเอกสารของงานราชการ ตามเจตนาของผู้บัญญัติ ซึ่งคำศัพท์ที่เกิดจากวิธีการเช่นนี้จะเรียกว่า ศัพท์บัญญัติ โดยทั่วแล้วศัพท์บัญญัติมักจะมาจากภาษาอังกฤษ

$เรียนออนไลน์ คณิตศาสตร์$

กราฟของสมการเชิงเส้นสองตัวแปร (จุดตัดแกน x และจุดตัดแกน y)

เนื้อหาในบทนี้จะเป็นการกล่าวถึง การแสดงความสัมพันธ์ของปริมาณสองปริมาณแล้วนำมาเขียนแสดงเป็นกราฟโดยใช้วิธีการหาจุดตัดของแกน x และ แกน y

จุด : เรขาคณิตวิเคราะห์

สารบัญ

จุด