จำนวนจริงในรูปกรณฑ์

จำนวนจริงในรูปกรณฑ์ หรือราก เขียนแทนด้วย อ่านว่า รากที่ n ของ x หรือ กรณฑ์ที่ n ของ x

เราจะบอกว่า จำนวนจริง a เป็นรากที่ n ของ x ก็ต่อเมื่อ

เช่น

2 เป็นรากที่ 2 ของ 4 เพราะ 2²  = 4 นั่นคือ   (รากที่สองของ 4 คือ 2 )

-2 เป็นรากที่ 2 ของ 4 เพราะ (-2)² = 4 นั่นคือ (รากที่สองของ 4 คือ -2)

ดังนั้น จะได้ว่า รากที่สองของ 4 คือ ±2 หรือเขียนอีกอย่างคือ นั่นเอง

**รากที่ 2 เรานิยมใช้  แต่ถ้าเป็นรากที่ n เมื่อ n มากกว่า 2 เราจะใช้ **

เช่น รากที่ 3 ของ x เขียนได้ดังนี้

สมบัติของ จำนวนจริงในรูปกรณฑ์

ให้ k, m, n เป็นจำนวนเต็มบวกที่มากกว่าหรือเท่ากับ 2

1.) 

เช่น 

2.) 

เช่น 

3.)    ; y ≠ 0

เช่น 

4.) 

เช่น 

5.) 

เช่น 

**ถ้า n เป็นจำนวนเต็มบวกที่เป็นเลขคู่ ตัวที่อยู่ใน ราก หรือ √‾ ต้องเป็นจำนวนจริงที่ไม่เป็นลบ

แต่ถ้า n เป็นจำนวนเต็มบวกที่เป็นเลขคี่ ตัวที่อยู่ในราก จะเป็นจำนวนจริงใดๆ**

จำนวนจริงในรูปเลขยกกำลัง

จำนวนจริงในรูปเลขยกกำลัง จะเขียนอยู่ในรูป xª เมื่อ x เป็นจำนวนจริงใดๆ และ a เป็นจำนวนเต็มบวก

xª = x⋅x⋅x⋅…⋅x (a ครั้ง)ฃ

x เป็นเลขฐาน

a เป็นเลขชี้กำลัง

เช่น 5³  : 5 เป็นเลขฐาน และ 3 เป็นเลขชี้กำลัง เป็นต้น

สมบัติของเลขยกกำลัง

ให้ x, y เป็นจำนวนจริงใดๆ m, n เป็นจำนวนเต็มบวก

1.)    (เลขฐานเหมือนกัน เมื่อคูณกันสามารถนำเลขชี้กำลังมาบวกกันได้)

เช่น 

2.) 

เช่น 

3.) 

เช่น 

4.) 

เช่น 

5.) ก็ต่อเมื่อ m = n

เช่น    ดังนั้น  x = 4

ความสัมพันธ์ระหว่างจำนวนจริงที่มีเลขชี้กำลังกับจำนวนจริงในรูปกรณฑ์

ให้ m, n เป็นจำนวนเต็มบวก โดยที่ n มากกว่าหรือเท่ากับ 2 และให้ x เป็นจำนวนจริงที่ไม่เป็นลบ

จะได้ว่า

1.) 

2.) 

3.)  

จากข้อ 2 และ 3 จะได้ว่า

การหารากที่สองของจำนวนที่อยู่ในรูป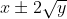

ให้ a, b เป็นจำนวนจริงบวกที่ a + b = x และ ab = y จะได้ว่า

1.) รากที่สองของ   คือ  นั่นคือ

2.) รากที่สองของ   คือ นั่นคือ

ตัวอย่างโจทย์เกี่ยวกับ จำนวนจริงในรูปกรณฑ์

1.) จงหาค่าของ

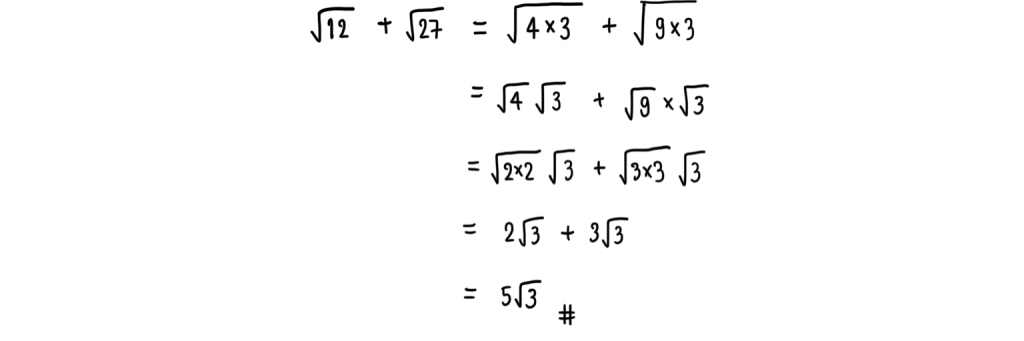
2.) จงหาค่าของ

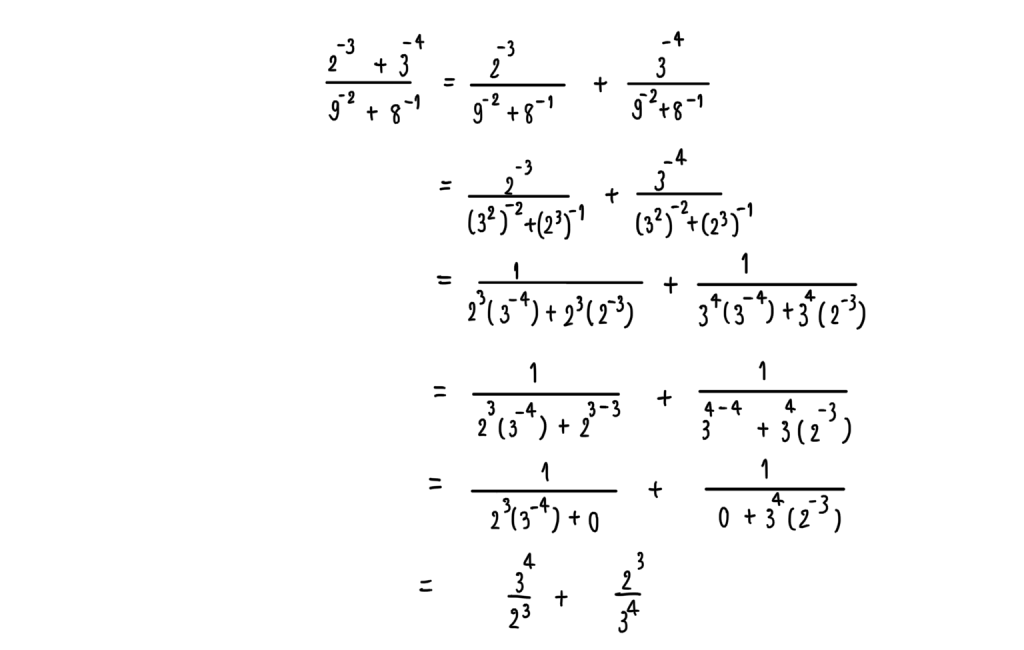
3.) จงหารากที่สองของ

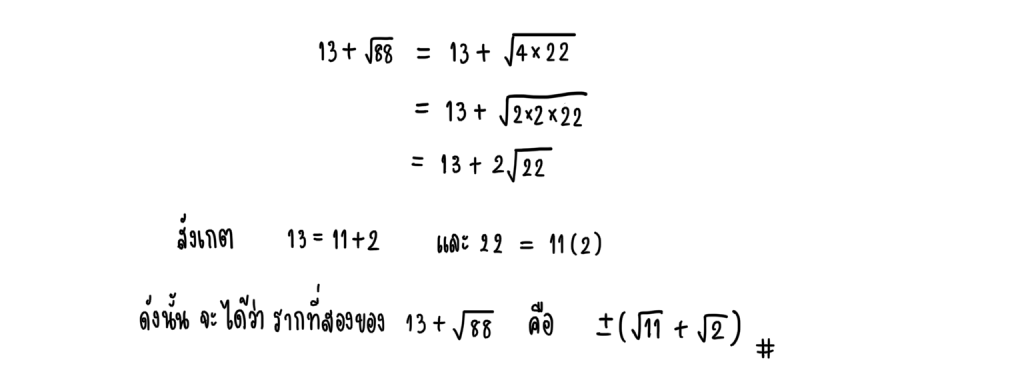
4.) หาค่า x ที่ทำให้

วีดิโอที่เกี่ยวข้องกับ จำนวนจริงในรูปกรณฑ์ และจำนวนจริงในรูปเลขยกกำลัง