การประยุกต์ของการแปลงทางเรขาคณิตเป็นการเปลี่ยนตำแหน่งของรูปเรขาคณิต โดยลักษณะและขนาดของรูปยังคงเดิม โดยใช้การหมุนเช่นเดียวกับการที่เราเคลื่อนที่ของสิ่งของโดยการหมุนไปในทิศทางตามเข็มนาฬิกาหรือทวนเข็มนาฬิกา
รูปแบบการหมุน
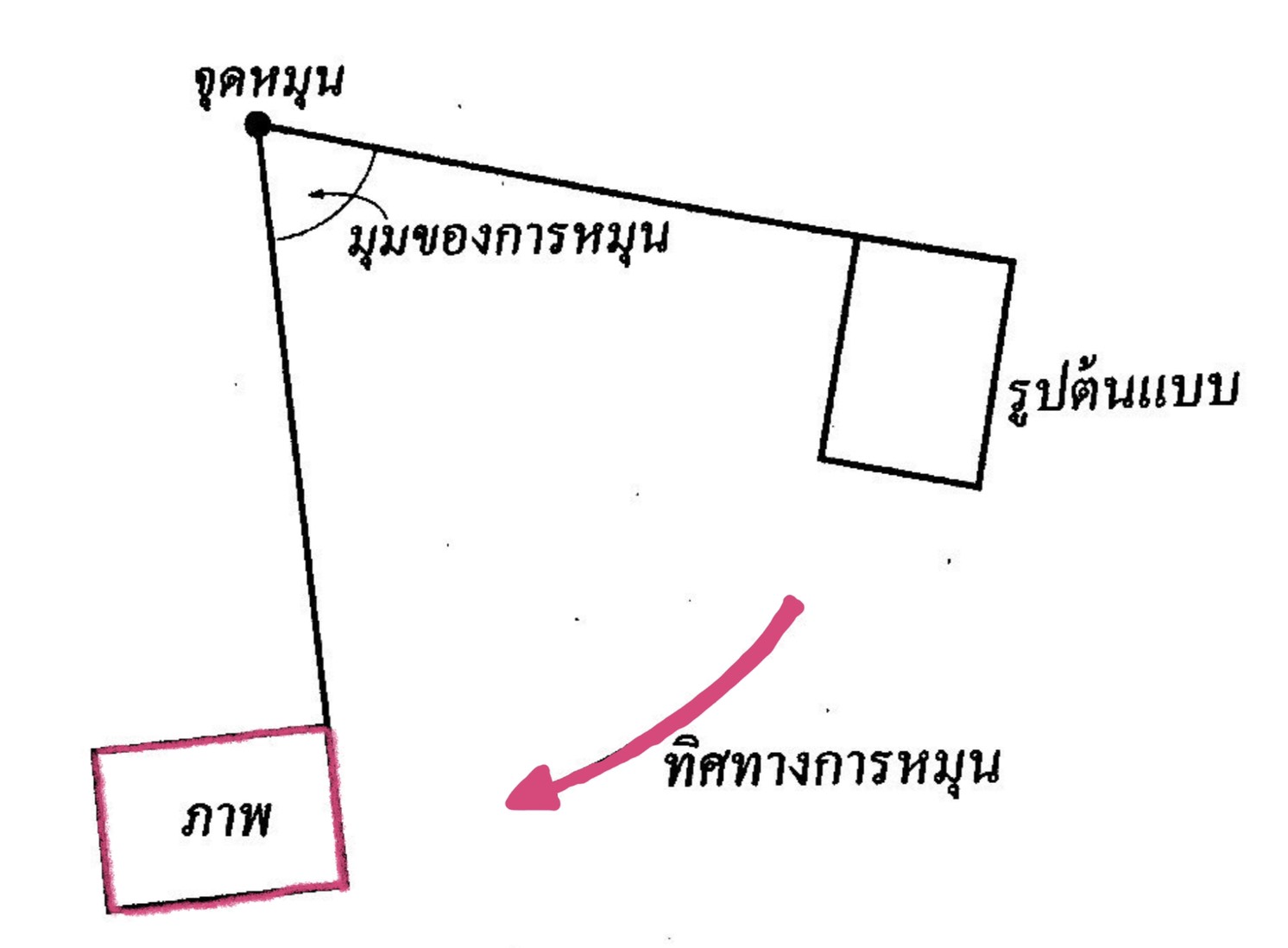
การหมุนบนระนาบเป็นการแปลงทางเรขาคณิตที่มีจุด O ที่ตรึงจุดหนึ่งเป็นจุดหมุนแต่ละจุด P บนระนาบมีจุด P เป็นภาพที่ได้จากการหมุนจุด P รอบจุด O ตามทิศทางที่กำหนดด้วยมุมที่มีจุดขนาด k โดยที่
- ถ้าจุด P ไม่ใช่จุด O แล้ว OP = OP’ และขนาดของ PÔP’ = k
- ถ้าจุด P เป็นจุดเดียวกันกับจุด O แล้ว P เป็นจุดหมุน
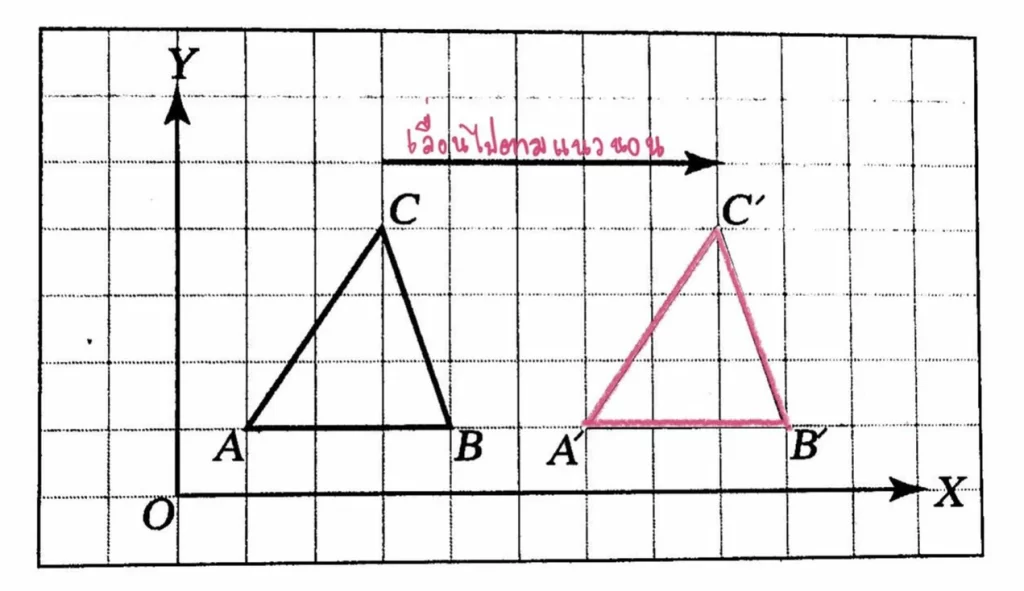
ตัวอย่างภาพที่เกิดจากการหมุน
สมบัติการหมุน
- สามารถเลื่อนรูปต้นแบบทับภาพที่ได้จากการหมุนได้สนิทโดยไม่ต้องพลิกรูปหรือกล่าวได้ว่ารูปต้นแบบกับภาพที่ได้จากการหมุนเท่ากันทุกประการ
- ส่วนของเส้นตรงบนรูปต้นแบบและภาพที่ได้จากการหมุนส่วนของเส้นตรงนั้นไม่จำเป็นต้องขนานกันทุกคู่
- จุดบนรูปต้นแบบและภาพที่ได้จากการหมุนจุดนั้นแต่ละคู่จะอยู่บนวงกลมที่มีจุดหมุนเป็นจุดศูนย์กลางเดียวกัน แต่วงกลมเหล่านี้ไม่จำเป็นต้องมีรัศมียาวเท่ากัน
การพิจารณาว่ารูปที่กำหนดให้เป็นผลจากการหมุนรูปอีกรูปหนึ่งหรือไม่สามารถพิจารณาตามเงื่อนไข 2 ข้อคือ
- สามารถเลื่อนรูปหนึ่งไปทับอีกรูปหนึ่งได้สนิทโดยไม่ต้องมีการพลิกรูป
- สามารถหาจุดหมุนทิศทางการหมุนและขนาดของมุมที่หมุนได้
ถ้าผลจากการแปลงสอดคล้องกับเงื่อนไขทั้งสองข้อแล้วการแปลงนั้นจัดเป็นการหมุนถ้าไม่สอดคล้องกับข้อใดข้อหนึ่งถือว่าไม่ใช่การหมุน
การหาภาพจากการหมุน
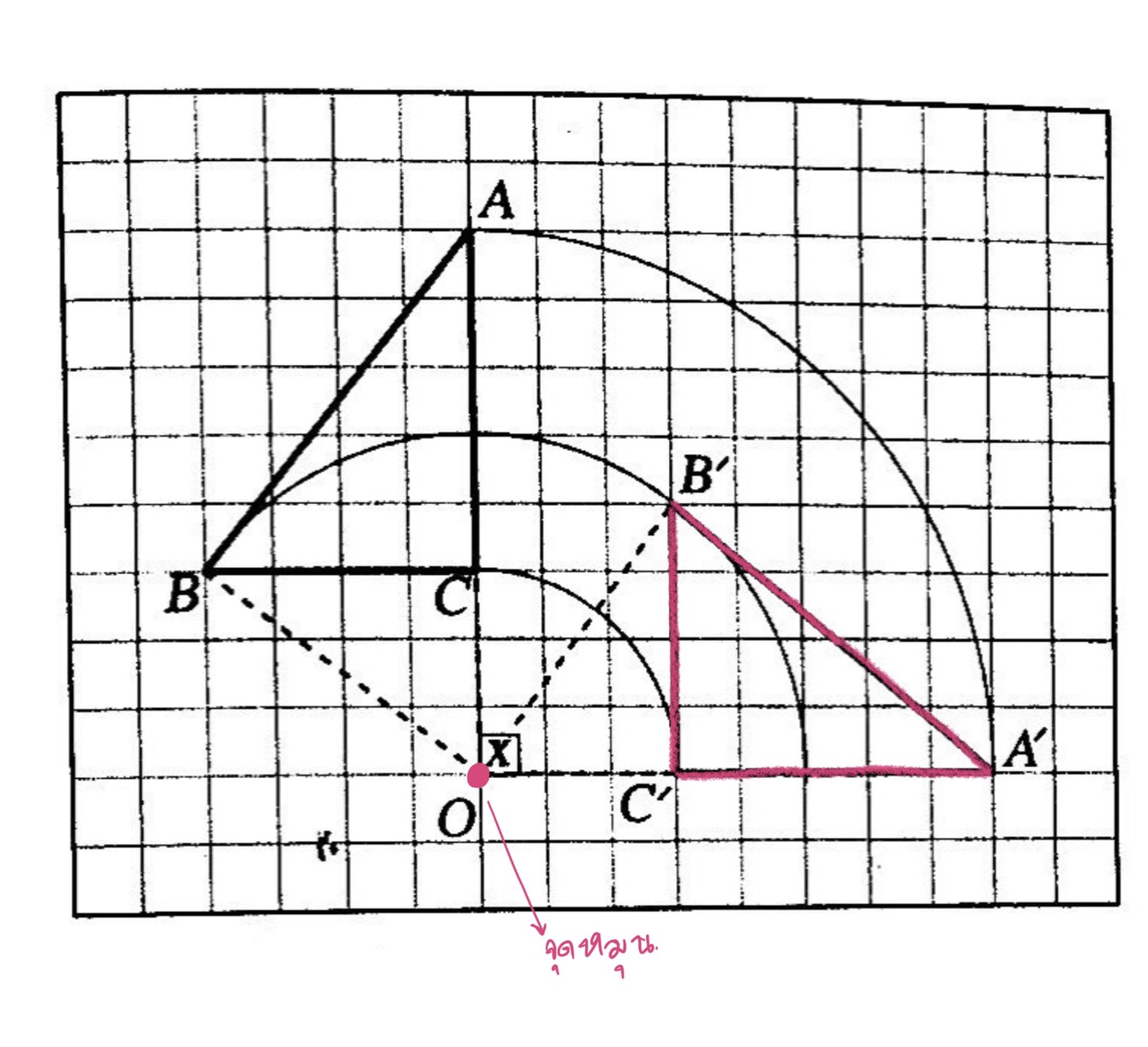
ตัวอย่างที่ 1 การหาภาพของ สามเหลี่ยมABC ที่เกิดจากการหมุนรอบจุด O ซึ่งไม่อยู่ในรูปสามเหลี่ยมไปการหาภาพจากการหมุน 90°ทิศตามเข็มนาฬิกา
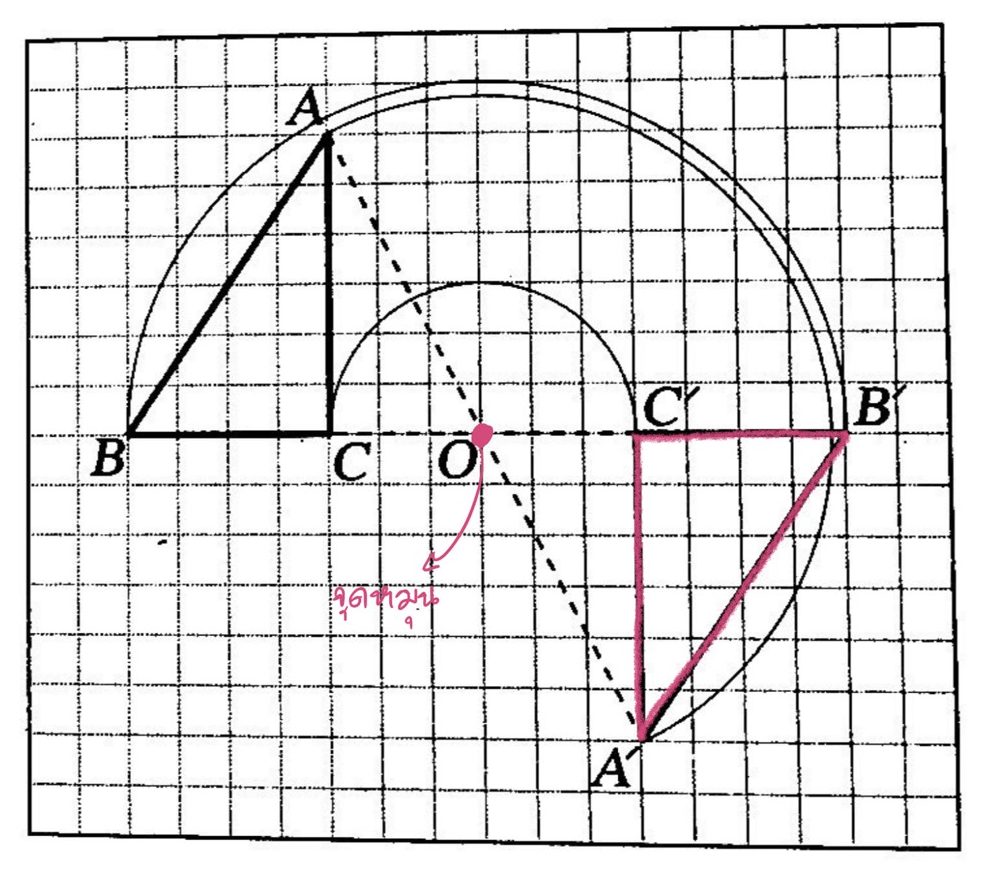
ตัวอย่างที่ 2 การหาภาพของ สามเหี่ยมABC ที่เกิดจากการหมุนรอบจุด O ซึ่งไม่อยู่ใน สามเหลี่ยมABC โดยหมุนไป 180°ทิศตามเข็มนาฬิกา
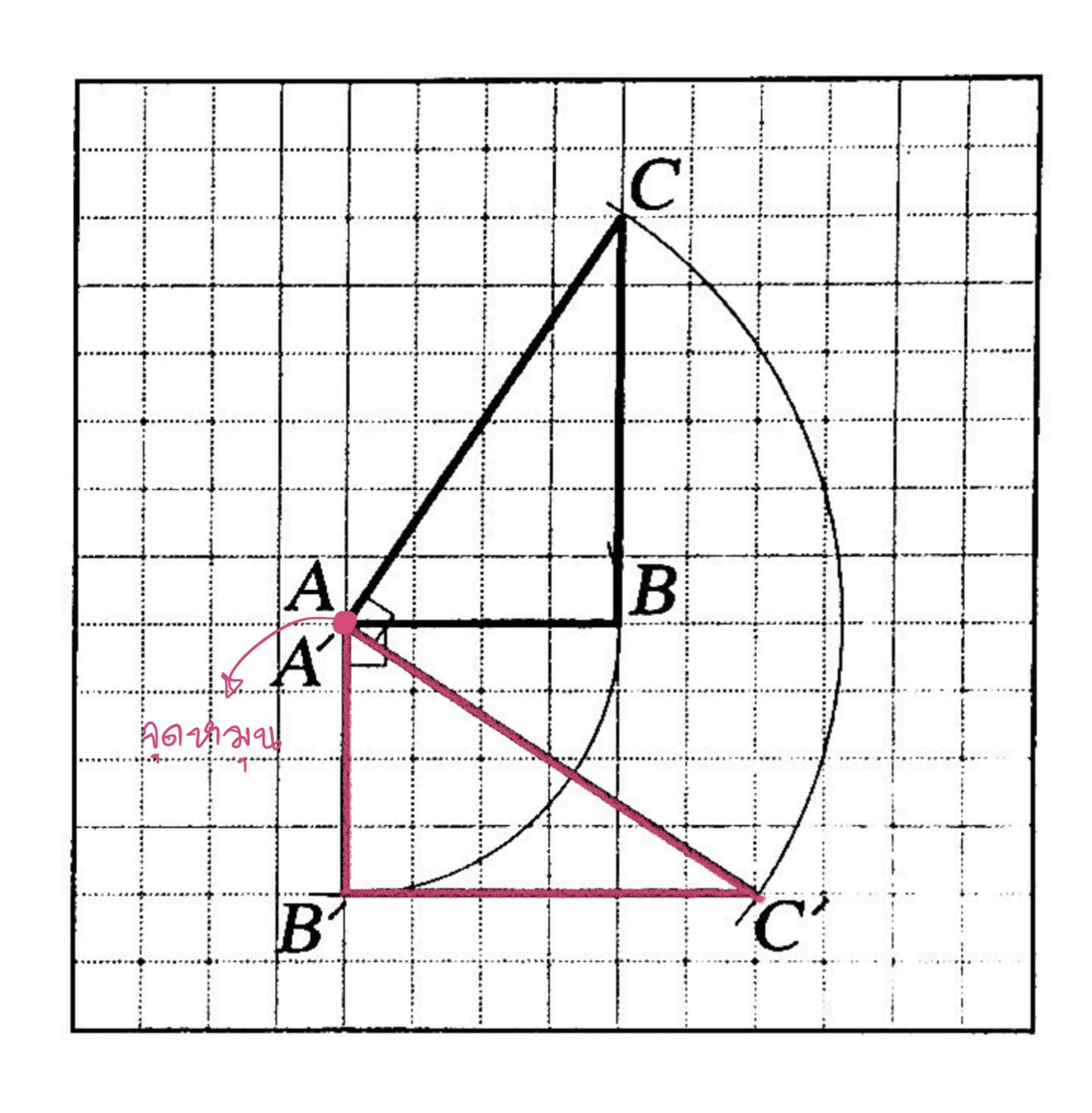
ตัวอย่างที่ 3 การหาภาพการหมุน สามเหลี่ยมABC รอบจุด A ทิศตามเข็มนาฬิกาไป 90°ทิศตามเข็นนาฬิกา
การหาจุดหมุนและทิศทางการหมุน
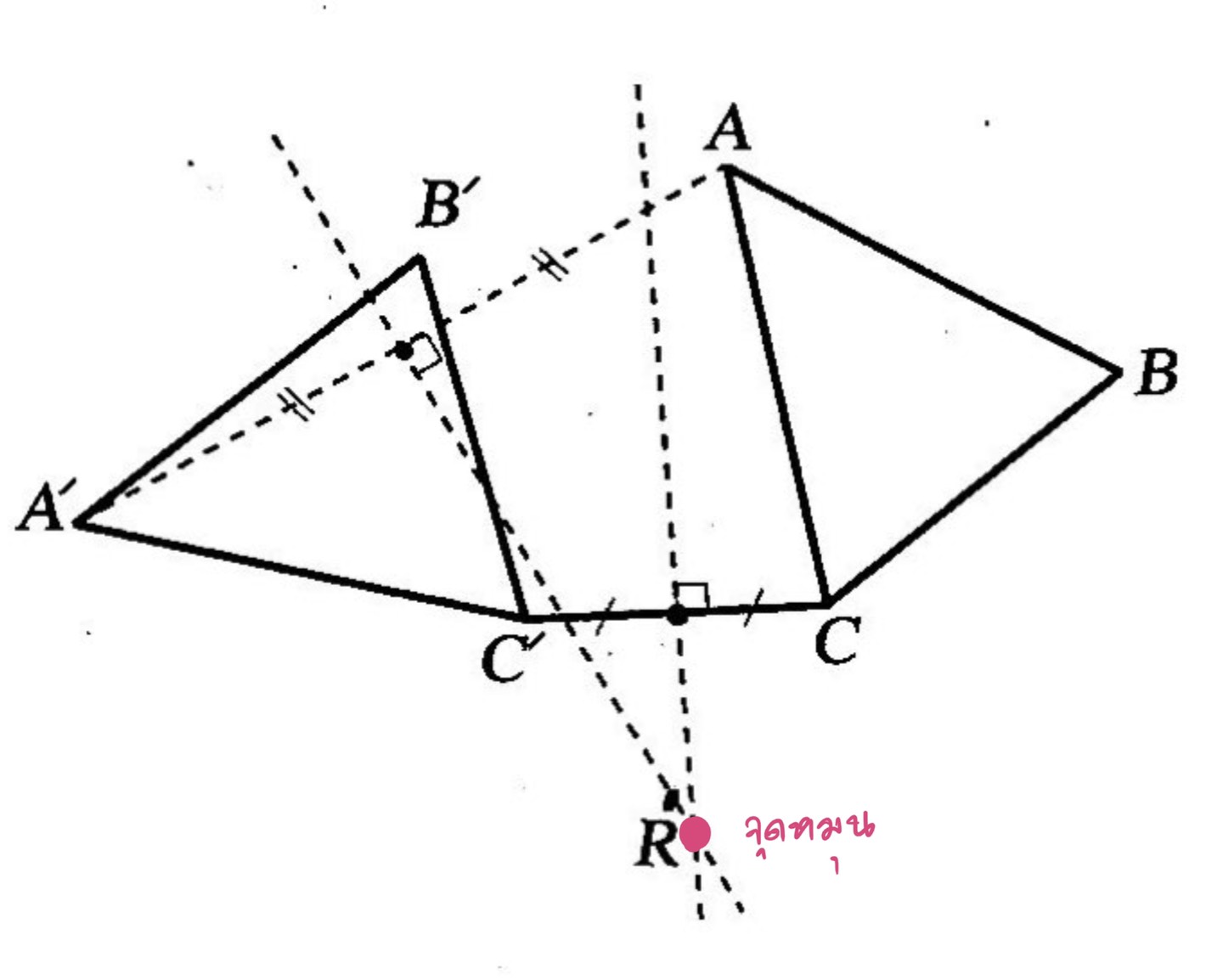
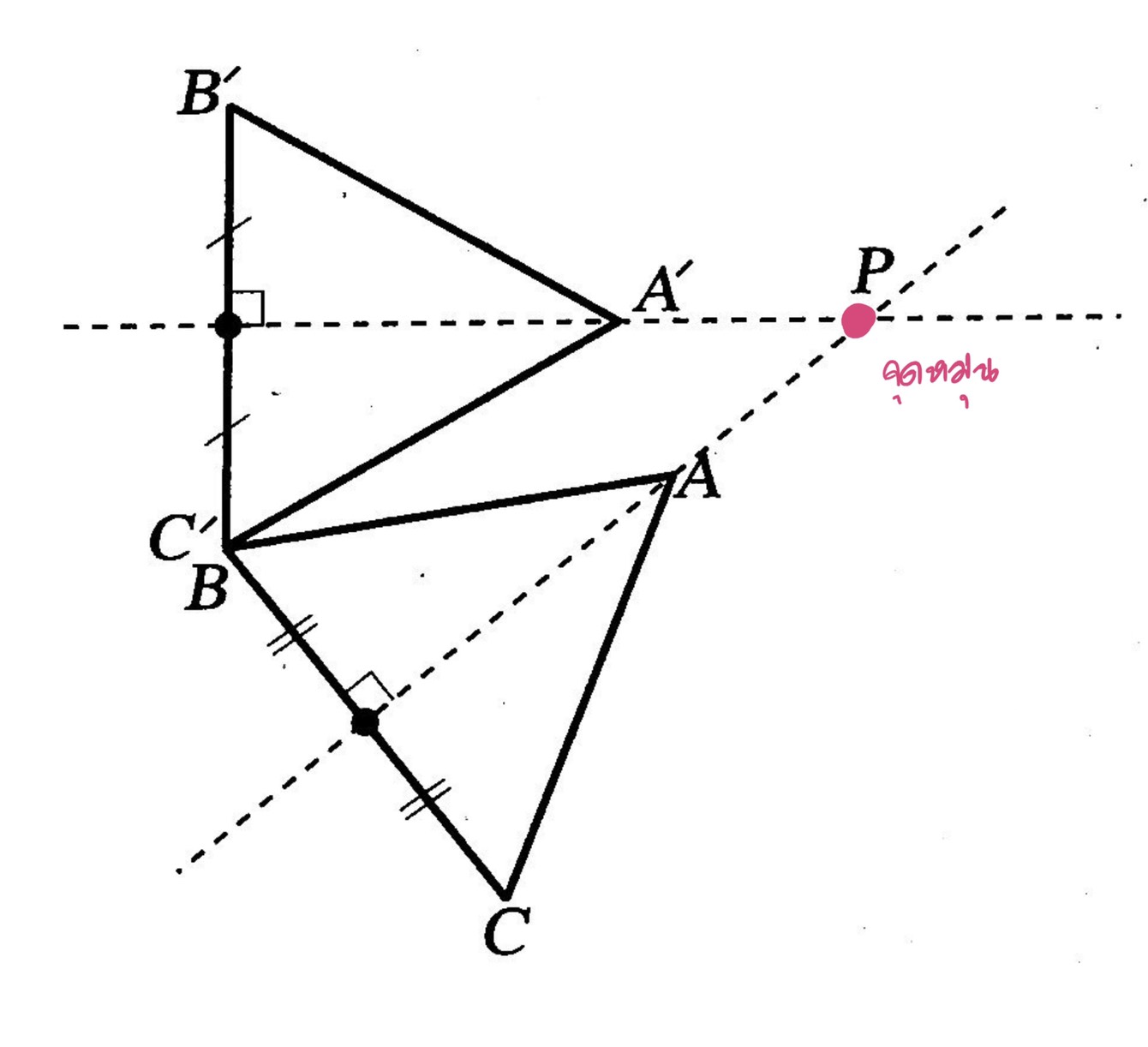
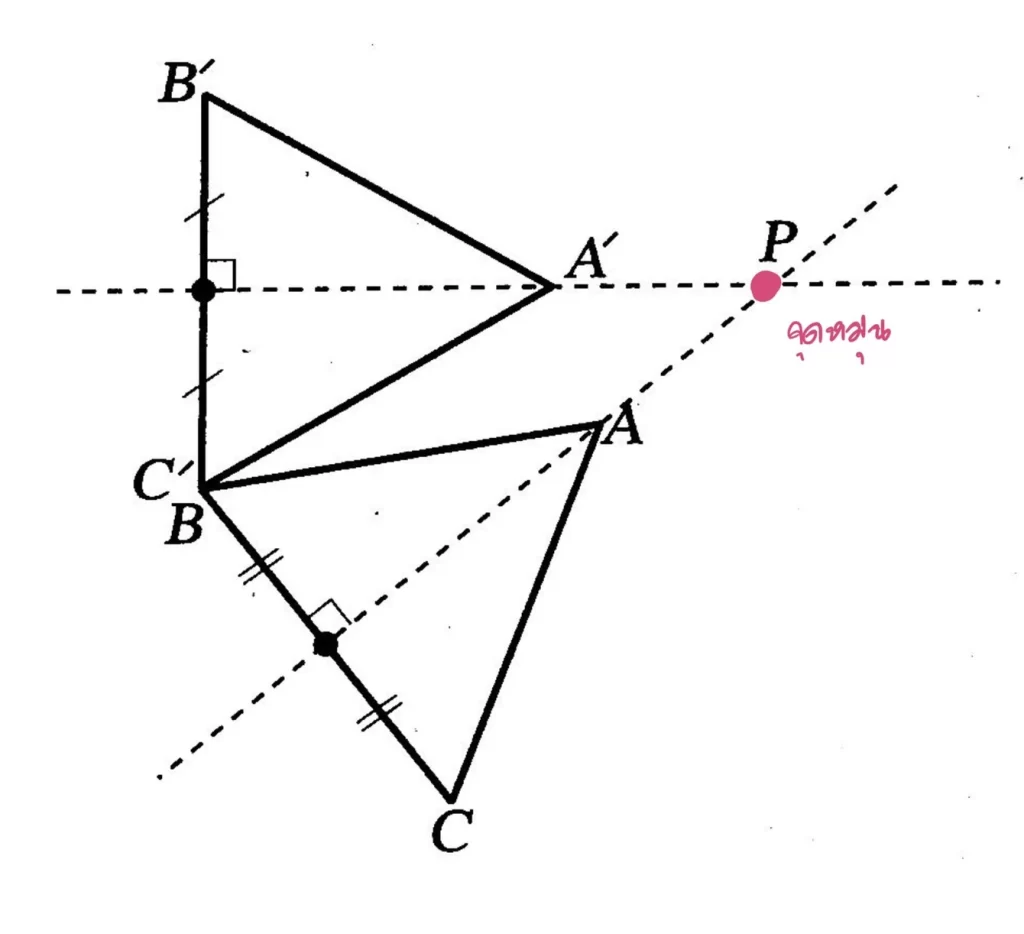
ตัวอย่าง กำหนด สามเหลี่ยมA’B’C’ เป็นภาพที่ได้จากการหมุน สามเหลี่ยมABC จงหาจุดหมุนและทิศทางการหมุน
แนวคิด การหาจุดหมุนทำได้โดยการสร้างเส้นตรงสองเส้นให้แต่ละเส้นตั้งฉากกันและแบ่งครึ่งซึ่งกันและกันกับส่วนของเส้นตรงที่เชื่อมระหว่างจุดที่สมนัยกันบนรูปต้นแบบและบนภาพที่ได้จากการหมุนจุดตัดของเส้นตรงทั้งสองคือจุดหมุนดังรูป