ดีเทอร์มิแนนต์
ดีเทอร์มิแนนต์ (Determinant) คือ ค่าของตัวเลขที่สอดคล้องกับเมทริกซ์จัตุรัส ถ้า A เป็นเมทริกซ์จัตุรัส จะเขียนแทนดีเทอร์มิแนนต์ของ A ด้วย det(A) หรือ
โดยทั่วไปการหาค่าดีเทอร์มิแนนต์ที่เจอในข้อสอบจะไม่เกินเมทริกซ์ 3×3 เพราะถ้ามากกว่า 3 แล้ว จะเริ่มมีความยุ่งยาก
**ค่าของดีเทอร์มิแนนต์จะเป็นจำนวนจริงและมีเพียงค่าเดียวเท่านั้นที่จะสอดคล้องกับเมทริกซ์จัตุรัส เช่น เมทริกซ์ B ก็จะมีค่าดีเทอร์มิแนนต์เพียงค่าเดียวเท่านั้น**
การหาค่าดีเทอร์มิแนนต์ของเมทริกซ์ขนาด 2×2

หลักการจำคือ คูณลง ลบ คูณขึ้น
เช่น
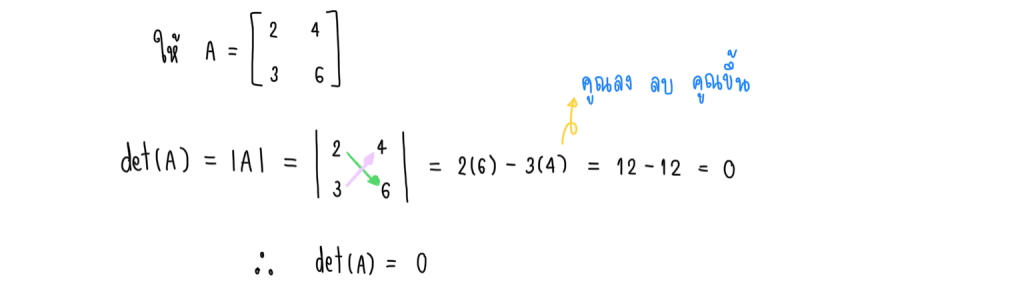
การหาค่าดีเทอร์มิแนนต์ของเมทริกซ์ขนาด 3×3
การหาค่าดีเทอร์มิแนนต์ของเมทริกซ์ 3×3 จะซซับซ้อนกว่า 2×2 นิดหน่อย แต่ยังใช้หลักการเดิมคือ คูณลง ลบ คูณขึ้น และสิ่งที่เพิ่มมาก็คือ การเพิ่มจำนวนหลักเข้าไปอีก 2 หลัก ซึ่งหลักที่เพิ่มนั้นก็คือค่าของ 2 หลักแรกนั่นเอง
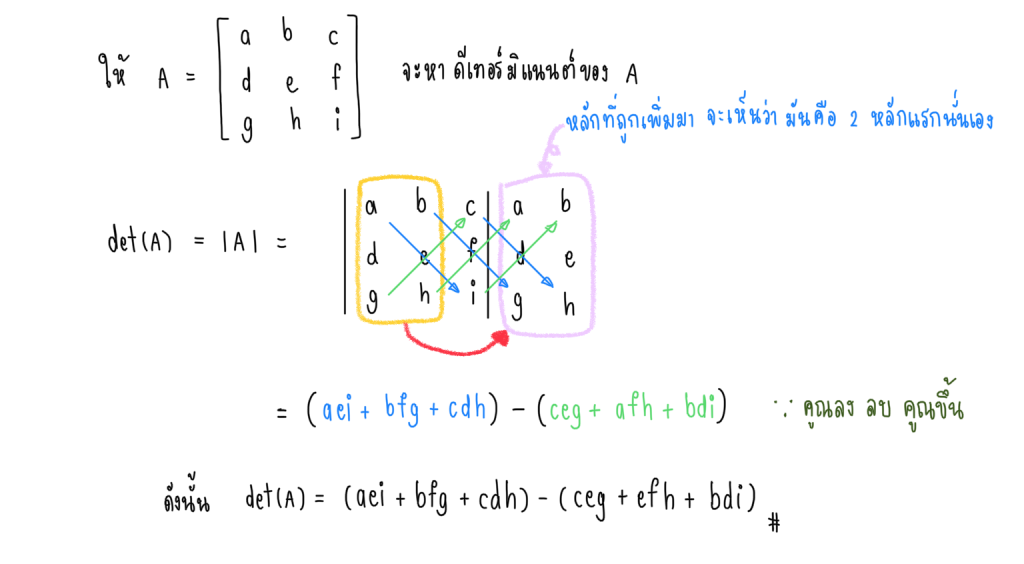
ตัวอย่างเมทริกซ์ขนาด 3×3

สมบัติเกี่ยวกับ ดีเทอร์มิแนนต์
ให้ A, B เป็นเมทริกซ์ขนาด n×n
1.) โดยที่
คือ เมทริกซ์สลับเปลี่ยน
2.) ถ้า สมาชิกแถวใดแถวหนึ่ง (หรือหลักใดหลักหนึ่ง) เป็น 0 ทุกตัว จะได้ว่า
เช่น
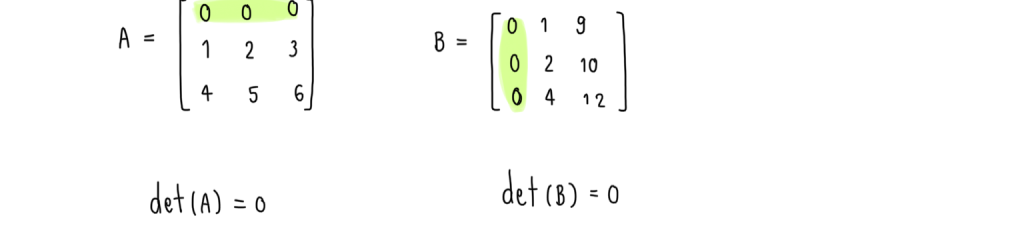
3.) ถ้า B คือเมทริกซ์ที่เกิดจากการสลับแถว (หรือหลัก) ของ A เพียงคู่เดียว จะได้ว่า
เช่น

4.) ถ้า B เกิดจากการคูณค่าคงตัว c ในสมาชิกแถวใดแถวหนึ่ง (หลักใดหลักหนึ่ง) ของ A จะได้ว่า
เช่น

5.)
6.) และ
7.)
เช่น

8.) A เป็นเมทริกซ์เอกฐาน ก็ต่อเมื่อ
9.) A เป็ยเมทริกซ์ไม่เอกฐาน ก็ต่อเมื่อ
10.) ถ้า A เป็นเมทริกซ์ไม่เอกฐาน แล้วจะได้ว่า
11.) ถ้า c เป็นค่าคงตัว จะได้ว่า (n คือมิติของเมทริกซ์ A)
เช่น

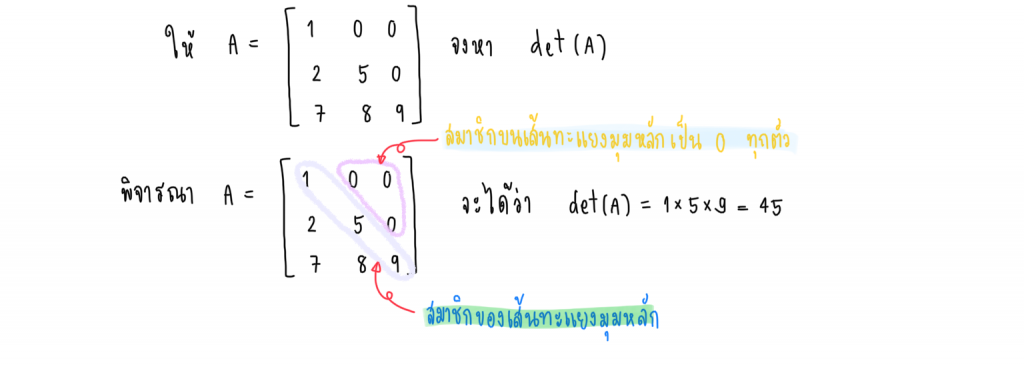
12.) สามเหลี่ยมล่าง และสามเหลี่ยมบน
ถ้า สมาชิกที่อยู่ใต้เส้นทะแยงมุมหลัก (หรือบนเส้นทะแยงมุมหลัก) เป็น 0 ทุกตัว จะได้ว่า ค่าดีเทอร์มิแนนต์จะเท่ากับ ผลคูณของสมาชิกเส้นทะแยงมุมหลัก
เช่น