การตรวจสอบความสมเหตุสมผล
การตรวจสอบความสมเหตุสมผล สามารถตรวจสอบได้หลายวิธี วิธีที่นิยมที่สุดคือ การตรวจสอบโดยใช้แผนภาพเวนน์-ออยเลอร์ โดยเราจะวาดแผนภาพตามเหตุทุกกรณีแล้วเราจะพิจารณาว่าเป็นไปตามผลสรุปที่โจทย์ให้มาหรือไม่
การให้เหตุผล
สมเหตุสมผล เมื่อแผนภาพแสดงผลสรุปตามที่กำหนดมา
ไม่สมเหตุสมผล เมื่อมีบางกรณีทำให้ผลสรุปไม่จริง
แผนภาพเวนน์-ออยเลอร์กับประโยคที่เจอบ่อย
ให้ A และ B เป็นเซตใดๆ
1.) สมาชิกทุกตัวของ A เป็นสมาชิกของ B
แปล ทุกตัวของ A อยู่ใน B
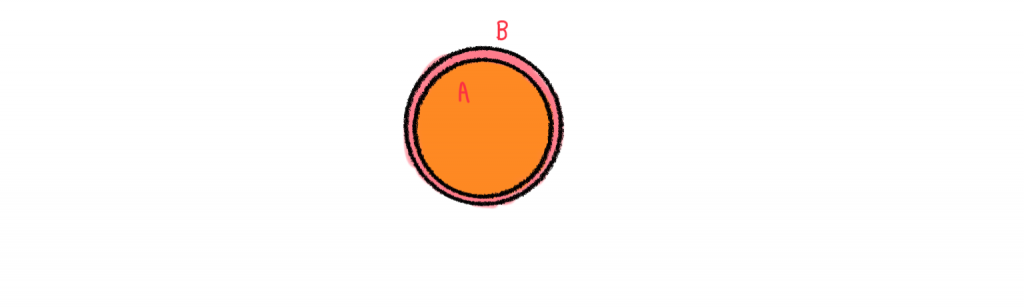
2.) ไม่มีสมาชิกใดใน A ที่เป็นสมาชิกของ B
แปล ไม่มี A ที่อยู่ใน B
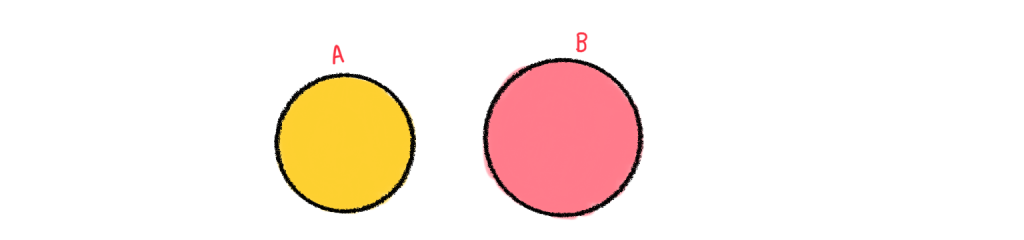
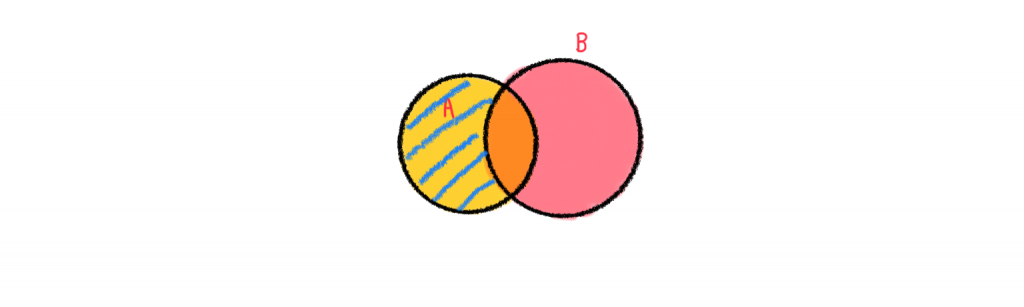
3.) สมาชิกบางตัวของ A เป็นสมาชิกของ B
แปล มีบางตัวของ A ที่อยู่ใน B
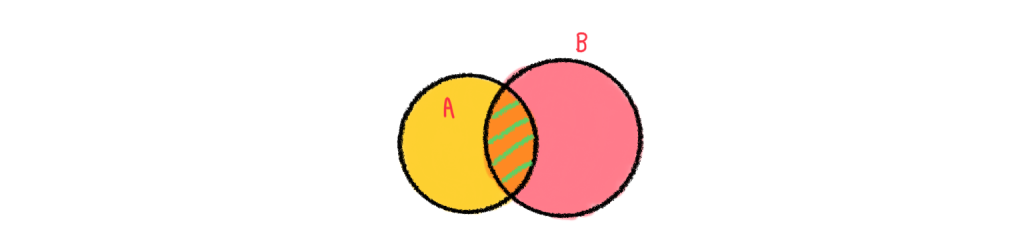
4.) มีสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B
แปล มีบางตัวของ A ที่ไม่อยู่ใน B แสดงว่า บางตัวก็ยังอยู่ใน B
ตัวอย่างการตรวจสอบความสมเหตุสมผล
1.)
เหตุ 1. นักกีฬาทุกคนสุขภาพดี
2. แป้งสุขภาพดี
ผล แป้งเป็นนักกีฬา
สิ่งแรกที่ต้องทำคือ พิจารณาว่าเซตไหนควรจะเป็นเซตที่ใหญ่ที่สุด
จากเหตุที่ 1 นักกีฬา “ทุกคน” สุขภาพดี แสดงว่า นักกีฬาจะต้องอยู่ในเซตของสุขภาพดี
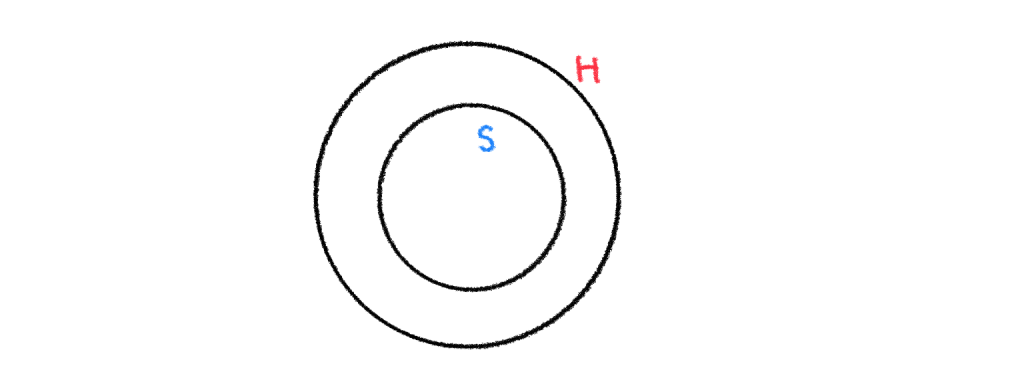
ให้ H เป็นเซตของสุขภาพดี และ S เป็นเซตของนักกีฬา
จากเหตุที่ 1 นำมาเขียนเป็นแผนภาพได้ ดังนี้
พิจารณาเหตุที่ 2 แป้งสุขภาพดี
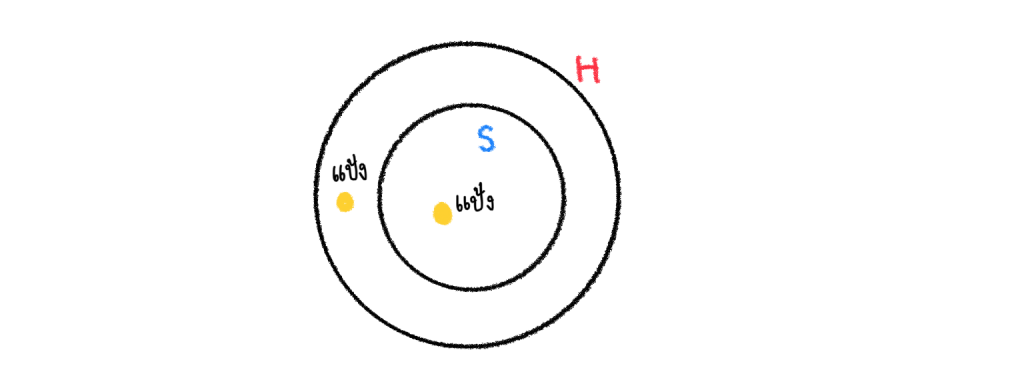
การที่แป้งสุขภาพดีนั้น แน่นอนว่าต้องอยู่ใน H แน่ๆ แต่แป้งอาจจะอยู่ใน S หรือไม่ก็ได้ ดังนั้น ผลสรุปที่บอกว่า แป้งเป็นนักกีฬาจึง ไม่สมเหตุสมผล เพราะแป้งไม่เป็นนักกีฬาก็ได้
2.)
เหตุ 1. สัตว์มีปีกบางตัวบินได้
2. สัตว์มีปีกทุกตัวมี 2 ขา
3. เป็ดเป็นสัตว์มีปีก
ผล เป็ดมี 2 ขา
เนื่องจากข้อนี้ เหตุที่ 1 ไม่มีคำว่า “ทุก” แต่มีคำว่า “บางตัว” ดังนั้น จะได้แผนภาพดังนี้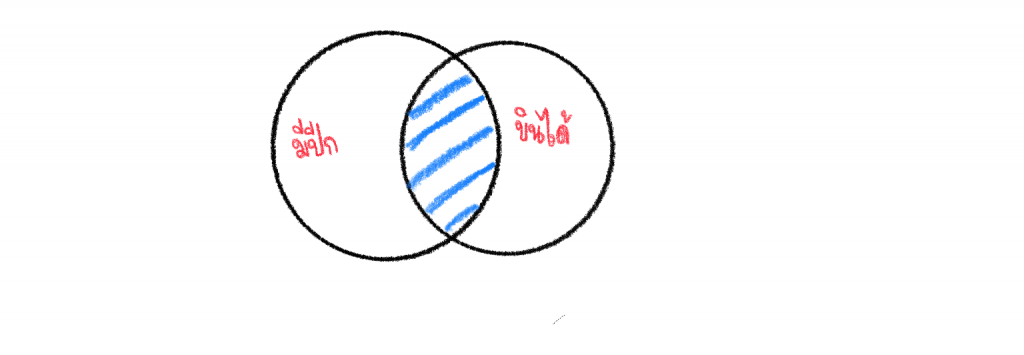
เหตุที่ 2 สัตว์มีปีกทุกตัวมี 2 ขา แสดงว่าเซตของ มีปีกอยู่ในเซตบอง มี 2 ขา เขียนแผนภาพได้ดังนี้
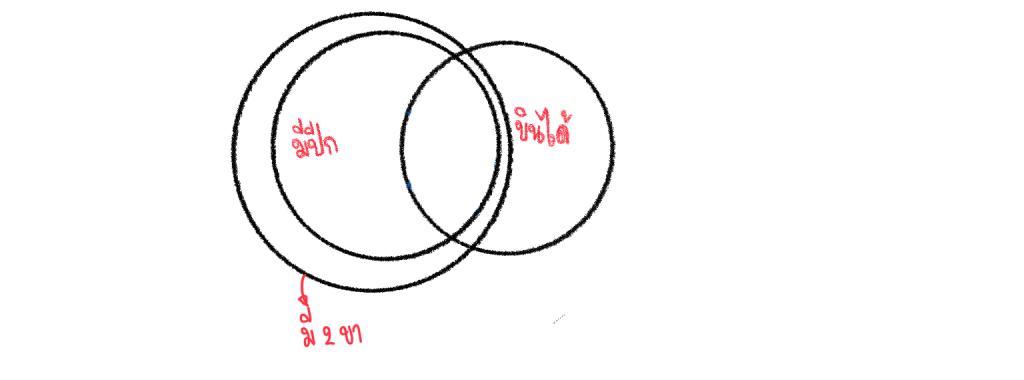
เหตุที่ 3 เป็นเป็นสัตว์มีปีก เขียนแผนภาพได้ดังนี้
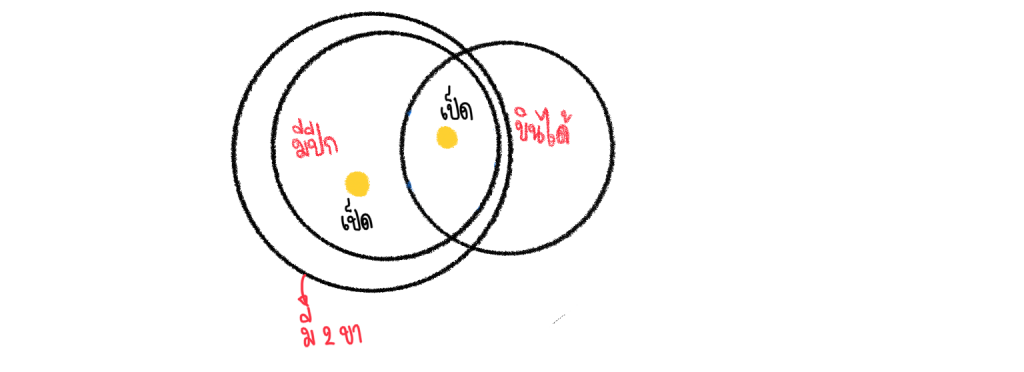
จะเห็นว่า เป็ดสามารถอยู่ได้ 2 ที่ คือ อาจจะบินได้ หรือไม่ได้ แต่ไม่ว่าจะอยู่ตรงไหน เป็ดก็ยังอยู่ในเซตของมี 2 ขาอยู่ดี ดังนั้น ข้อนี้จึง สมเหตุสมผล
3.)
เหตุ 1. สัตว์มีปีกบางตัวบินได้
2. สัตว์มีปีกทุกตัวมี 2 ขา
3. เป็ดเป็นสัตว์มีปีก
ผล เป็ดบินได้
โจทย์ข้อนี้จะเห็นว่าคือโจทย์เดียวกันกับข้อ 2 แต่ผลสรุปต่างกัน พิจารณาแผนภาพ ดังนี้

จะเห็นว่าเป็ดมี 2 จุด คืออยู่นอกวงกลมที่บินได้กับอยู่ในวงกลมบินได้ ดังนั้น ผลสรุปนี้ ไม่สมเหตุสมผล เพราะเป็ดอาจจะบินได้หรือบินไม่ได้ก็ได้
4.)
เหตุ 1. ทุกคนที่อ่านหนังสือ ทำข้อสอบได้
2. ธิดาสอบได้
ผล ธิดาอ่านหนังสือ
พิจารณาเหตุที่ 1 ทุกคนที่อ่านหนังสือ ทำข้อสอบได้ เขียนเป็นแผนภาพๆได้ดังนี้
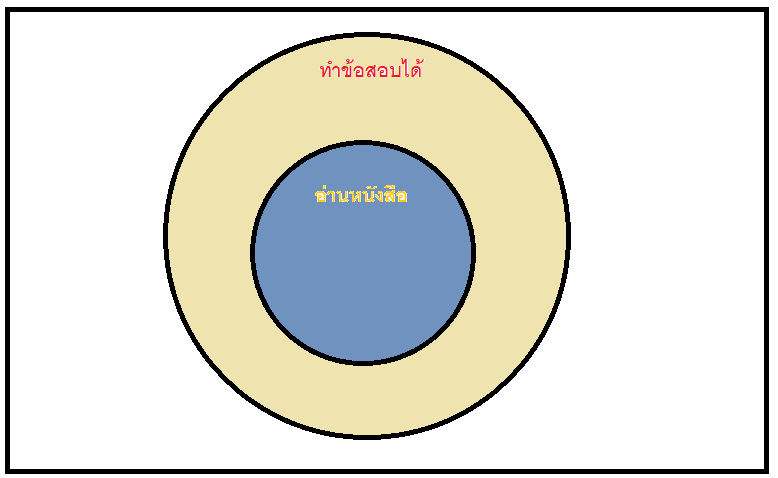
จากนั้นพิจารณาเหตุที่ 2 ธิดาสอบได้ เขียนเป็นแผนภาพได้ดังนี้
กรณีที่ 1 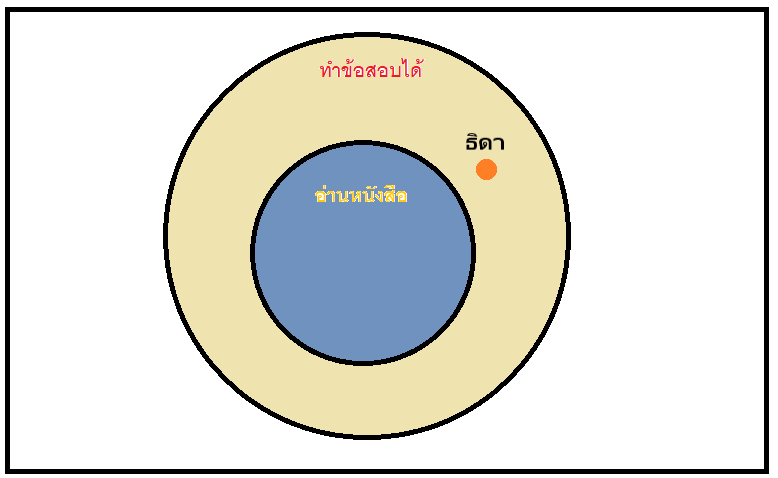
กรณีที่ 2 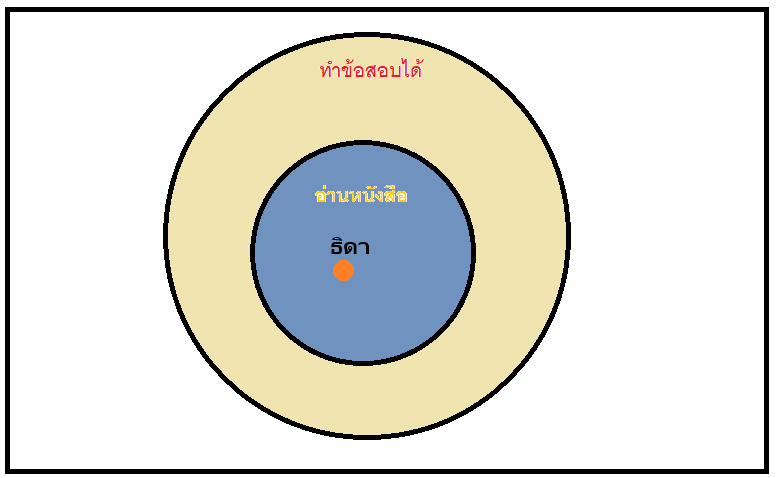
จากรูปจะเห็นว่าเป็นไปได้ 2 กรณี จะได้ว่า ธิดาไม่จำเป็นต้องอ่านหนังสือก็ได้
ดังนั้น การให้เหตุผลข้อนี้ ไม่สมเหตุสมผล
5.)
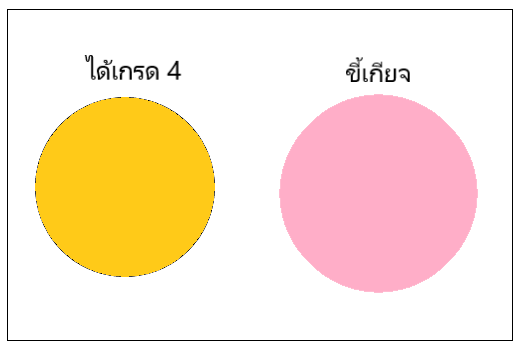
เหตุ 1. ไม่มีคนที่ได้เกรด 4 ที่ขี้เกียจ
2. สมาร์ทไม่ขี้เกียจ
ผล สมาร์ทได้เกรด 4
พิจารณาเหตุที่ 1 ไม่มีคนคนที่ไดเเกรด 4 ที่ขี้เกียจ เมื่อวาดเป็นแผนภาพจะได้เป็นวงกลม 2 วง ที่ไม่ซ้อนทับกัน
พิจารณาเหตุที่ 2 สมาร์ทไม่ขี้เกียจ เป็นได้ 2 กรณี ดังนี้
กรณีที่ 1 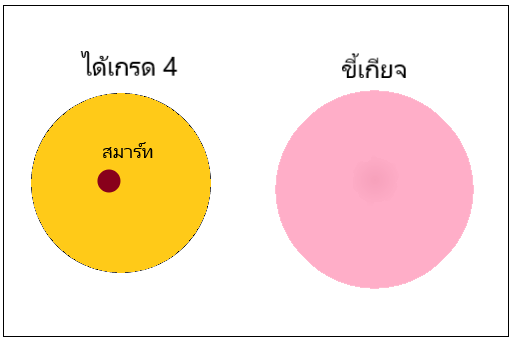
กรณีที่ 2 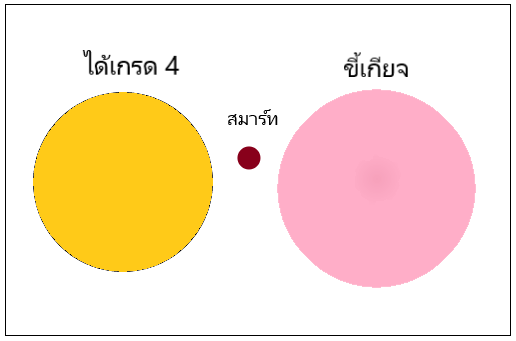
จะเห็นว่าการที่สมาร์ทไม่ขี้เกียจไม่จำเป็นจะต้องได้เกรด 4
ดังนั้นการให้เหตุผลข้อนี้ ไม่สมเหตุสมผล
วีดีโอ การตรวจสอบความสมเหตุสมผล
เนื้อหาที่เกี่ยวข้องกับการตรวจสอบความสมเหตุสมผล