บทความนี้ ได้รวบรวมเนื้อหาเรื่อง จำนวนตรงข้ามและค่าสัมบูรณ์ ซึ่งเป็นพื้นฐานในการบวกลบจำนวนเต็ม โดยก่อนหน้านี้น้องๆได้เรียนเรื่องการเปรียบเทียบจำนวนเต็มมาแล้ว ต่อไปจะพูดถึงค่าสัมบูรณ์ของจำนวนเต็มใดๆ จะหาได้จากระยะที่จำนวนเต็มนั้นอยู่ห่างจาก 0 บนเส้นจำนวน แต่ก่อนอื่นเรามาทำความรู้จักกับจำนวนตรงข้ามกันก่อนนะคะ

จำนวนตรงข้าม

      “หากค่าของจำนวนที่อยู่ห่างจาก 0 เท่ากัน แต่อยู่ต่างทิศทางกันมีค่าเท่ากันหรือไม่” (ค่าไม่เท่ากัน)       

     ทราบหรือไม่ว่า จำนวนที่อยู่ทิศทางต่างกันแต่มีระยะห่างจาก 0 เท่ากัน คือ จำนวนอะไร (จำนวนตรงข้าม) ยกตัวอย่าง ดังนี้

เช่น      จำนวนตรงข้ามของ 4 เขียนแทนด้วย -4

   จำนวนตรงข้ามของ -4 เขียนแทนด้วย -(-4)

    และเนื่องจากจำนวนตรงข้ามของ -4 คือ 4

ดังนั้น  -(-4) = 4

สรุปได้ว่า

ถ้า a เป็นจำนวนใดๆ จำนวนตรงข้าม ของ a มีเพียงจำนวนเดียวและเขียนแทนด้วย  – a  เรียก – a ว่า จำนวนตรงข้าม ของ a

ตัวอย่างที่ 1  จงเขียนจำนวนตรงข้ามของจำนวนต่อไปนี้

1.   -7 เป็นจำนวนตรงข้ามของ                        
2.                     เป็นจำนวนตรงข้ามของ    15
3.                     เป็นจำนวนตรงข้ามของ   -24
4.   0 เป็นจำนวนตรงข้ามของ                       
5.   32  เป็นจำนวนตรงข้ามของ                        

เฉลย

1.   -7    เป็นจำนวนตรงข้ามของ    7
2.   -15  เป็นจำนวนตรงข้ามของ    15
3.   24   เป็นจำนวนตรงข้ามของ    -24
4.   0     เป็นจำนวนตรงข้ามของ    0
5.   32   เป็นจำนวนตรงข้ามของ    -32     

ค่าสัมบูรณ์

พิจารณาเส้นจำนวนต่อไปนี้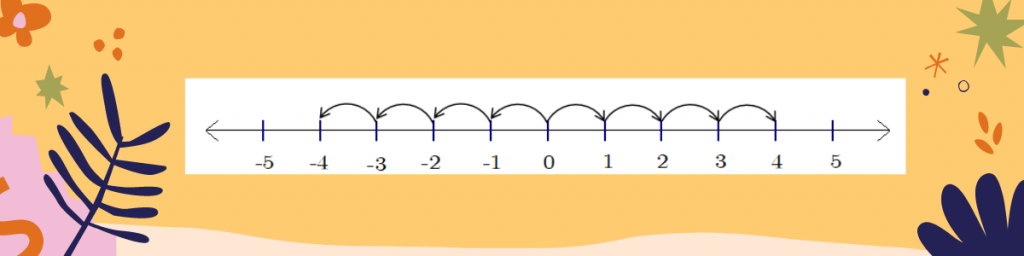

1.    ระยะห่างของจำนวนเต็มบนเส้นจำนวนเท่ากันหรือไม่ (เท่ากัน)
2.    -4 อยู่ห่างจาก 0 อยู่เท่าใด (4)
3.    4 อยู่ห่างจาก 0 อยู่เท่าใด (4)
4.    ระยะห่างของ -4 และ 4 อยู่ห่างจาก 0 เท่ากันหรือไม่ (เท่ากัน)

จะเห็นว่า 4 อยู่ห่างจาก 0 เป็นระยะ 4 หน่วย เรียกว่า  ค่าสัมบูรณ์ของ 4 เท่ากับ 4 เขียนแทนด้วย l4l = 4 

            -4 อยู่ห่างจาก 0 เป็นระยะ 4 หน่วย เรียกว่า  ค่าสัมบูรณ์ของ -4  เท่ากับ 4 เขียนแทนด้วย l-4l = 4 

สรุปได้ว่า

ค่าสัมบูรณ์ของจำนวนเต็มใดๆ คือ ระยะห่างของจำนวนเต็มนั้น กับ 0 (ศูนย์) บนเส้นจำนวน ดังนั้นค่าสัมบูรณ์ของจำนวนเต็มจึงเป็นบวกเสมอ โดยมีสัญลักษณ์ คือ l l  

ตัวอย่างที่ 2   3  อยู่ห่างจาก  0  เป็นระยะทางกี่หน่วย

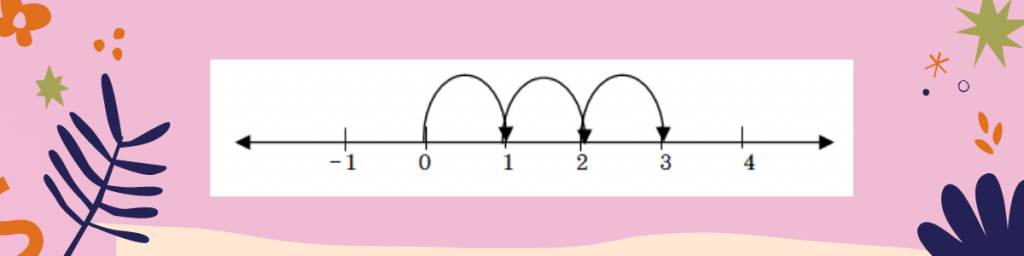
ตอบ 3  อยู่ห่างจาก  0  เป็นระยะทาง  3  หน่วย  กล่าวว่า  ค่าสัมบูรณ์ของ  3  เท่ากับ  3 หรือ l3l = 3 

ตัวอย่างที่ 3   -3  อยู่ห่างจาก  0  เป็นระยะทางกี่หน่วย

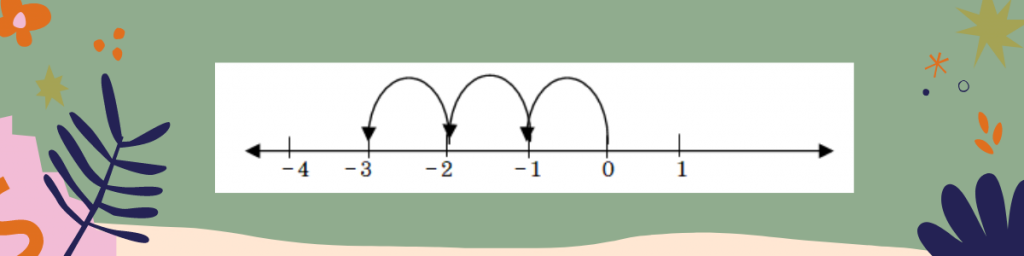
ตอบ  -3  อยู่ห่างจาก 0  เป็นระยะทาง  3  หน่วย  กล่าวว่า ค่าสัมบูรณ์ของ -3 เท่ากับ  3  หรือ l-3l = 3 

ตัวอย่างที่ 4   4 อยู่ห่างจาก 0 เป็นระยะ 4 หน่วย

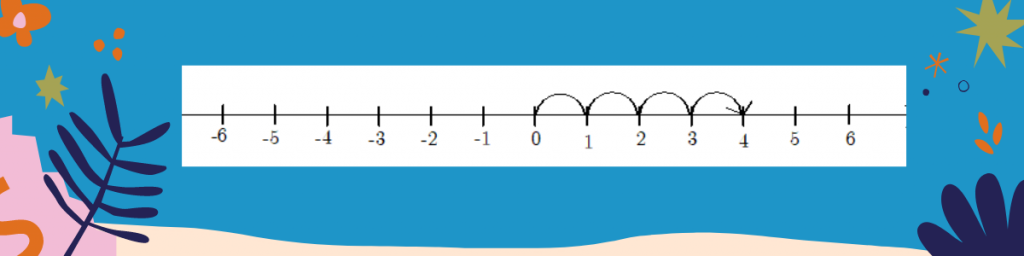
ตอบ 4  อยู่ห่างจาก 0  เป็นระยะทาง  4  หน่วย  กล่าวว่า ค่าสัมบูรณ์ของ 4 เท่ากับ 4 หรือ l4l = 4 

สรุป     ค่าสัมบูรณ์ของจำนวนเต็มใดๆ จะหาได้จากระยะทางที่จำนวนเต็มนั้นอยู่ห่างจาก 0 บนเส้นจำนวน

เมื่อน้องๆเรียนรู้เรื่อง จำนวนตรงข้ามและค่าสัมบูรณ์ จากตัวอย่างข้างต้น ทำให้สามารถหาจำนวนตรงข้ามและค่าสัมบูรณ์ของจำนวนเต็มใดๆได้  ลำดับต่อไปที่น้องๆต้องเรียนรู้คือ การบวกลบจำนวนเต็ม ซึ่งจะเป็นการฝึกน้องๆได้ฝึกการคิดวิเคราะห์ และบวกลบจำนวนเต็มได้อย่างรวดเร็วและแม่นยำ

คลิปวิดีโอ จำนวนตรงข้ามและค่าสัมบูรณ์

        คลิปวิดีโอนี้ได้รวบรวมวิธีการหา จำนวนตรงข้ามและค่าสัมบูรณ์  ไว้อย่างละเอียด ซึ่งเป็นคลิปสั้นๆ ที่สามารถเข้าใจได้ง่าย แฝงไปด้วยสาระความรู้ และเทคนิค รวมถึงการอธิบายตัวอย่างและสอนวิธีคิดที่จะทำให้วิชาคณิตศาสตร์เป็นเรื่องง่าย