ฟังก์ชันประกอบ

ฟังก์ชันประกอบ

ฟังก์ชันประกอบ คือฟังก์ชันที่เกิดจากการหาค่าฟังก์ชันที่ส่งจากเซต A ไปเซต C โดยที่ f คือฟังก์ชันที่ส่งจาก A ไปยัง B และ g เป็นฟังก์ชันที่ส่งจาก B ไปยัง C

เราเรียกฟังก์ชันที่ส่งจาก A ไป C นี้ว่า gof

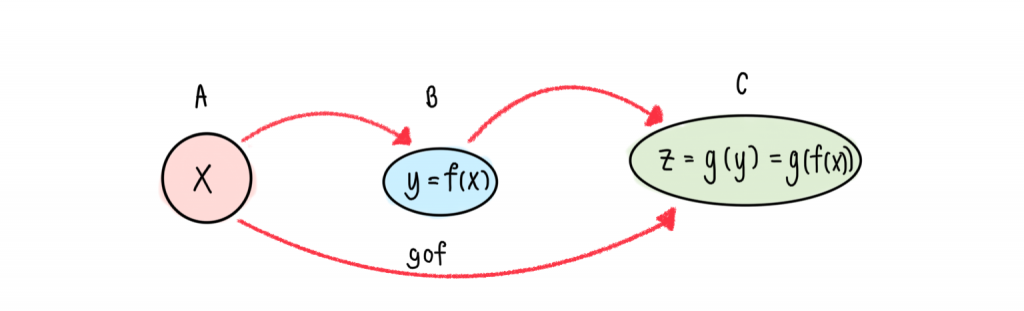
จากรูป จะเห็นว่า สมาชิกในเซต B นั้น เป็นทั้งเรนจ์ของ f และเป็นโดเมนของ g

ดังนั้น การที่จะหา gof ได้ y ต้องอยู่ในเรนจ์ของฟังก์ชัน f และ โดเมนของฟังก์ชัน g พร้อมๆกัน นั่นคือ $\mathrm{R_f \cap D_g \neq \varnothing}$

และจากรูปจะเห็นว่า

f เป็นความสัมพันธ์จาก A ไป B

g เป็นความสัมพันธ์จาก B ไป C

gof เป็นความสัมพันธ์จาก A ไป C

บทนิยาม

ให้ f และ g เป็นฟังก์ชัน และ $\mathrm{R_f \cap D_g \neq \varnothing}$ แล้วฟังก์ชันประกอบของ f และ g คือ gof โดยที่ gof(x) = g(f(x))

และ $\mathrm{D_{gof}}$ = {x ∈ $\mathrm{D_f}$ : f(x) ∈ $\mathrm{D_g}$}

เช่น

ให้ f = {(1, 2), (2, 4), (3, 3), (4, 5)} และ g = {(1, 3), (2, 5), (3, 2), (4, 4)} จงหา gof

ขั้นแรก คือเราต้องตรวจสอบก่อนว่า $\mathrm{R_f \cap D_g \neq \varnothing}$

$\mathrm{R_f}$ = {2, 3, 4, 5} และ $\mathrm{D_g}$ = {1, 2, 3, 4} ดังนั้น $\mathrm{R_f\cap D_g}$ = {2, 3, 4} นั่นคือ $\mathrm{R_f \cap D_g \neq \varnothing}$

ดังนั้น หา gof ได้

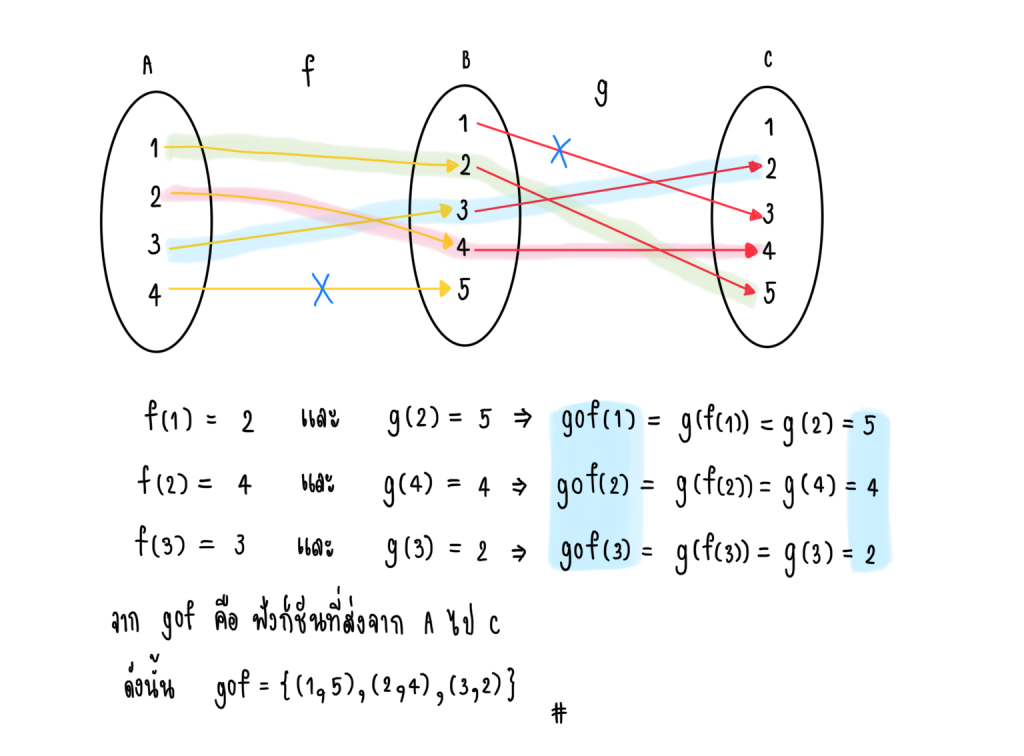
ตัวอย่างการหาฟังก์ชันประกอบ

ให้ f(x) = 2x – 3 และ g(x) = x² + 5

จงหา gof, fog, gof(2), fog(3)

พิจารณา $\mathrm{D_f}$ = $\mathbb{R}$ จะได้ว่า $\mathrm{R_f}$ = $\mathbb{R}$ และพิจารณา $\mathrm{D_g}$ = $\mathbb{R}$ จะได้ $\mathrm{R_g}=\mathbb{R}$

จาก $\mathrm{R_f}$ = $\mathbb{R}$ และ $\mathrm{D_g}$ = $\mathbb{R}$ จะได้ว่า $\mathrm{R_f \cap D_g \neq \varnothing}$ นั่นคือ หา gof ได้

จาก $\mathrm{R_g}=\mathbb{R}$ และ $\mathrm{D_f}$ = $\mathbb{R}$ จะได้ว่า $\mathrm{R_g\cap D_f} \neq \varnothing$ นั่นคือ หา fog ได้

gof

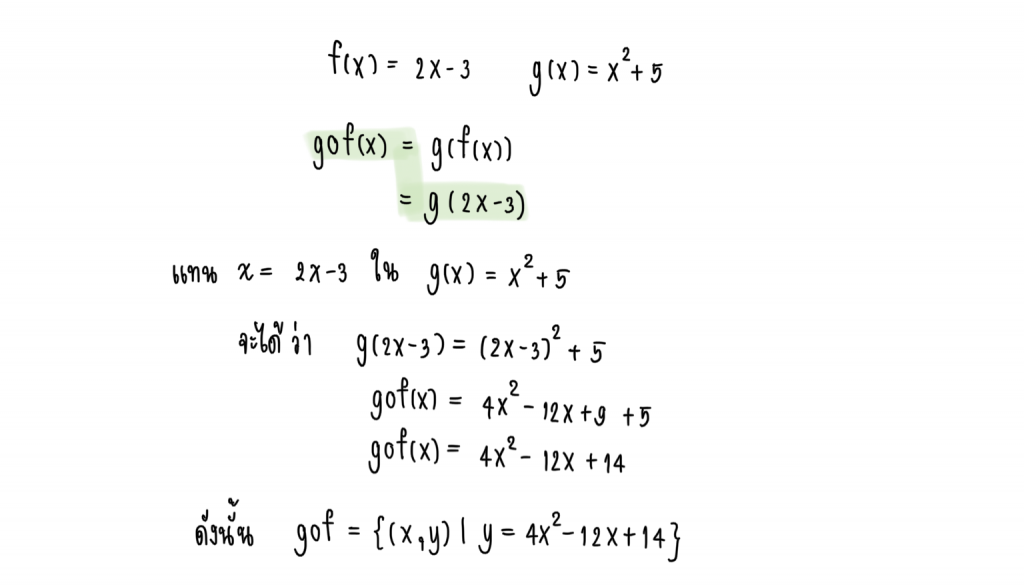fog

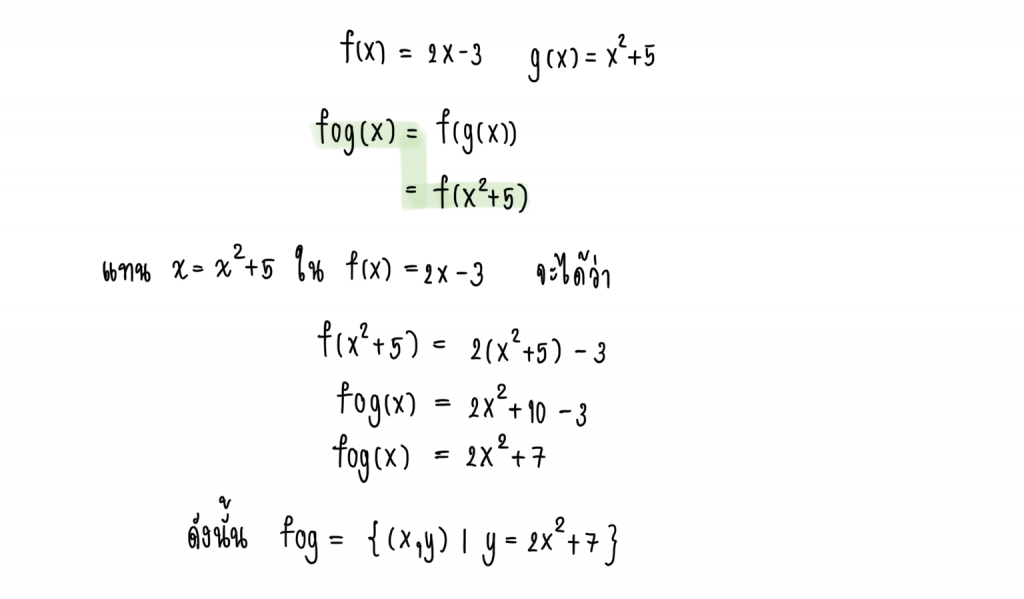
gof(2)

fog(3)